INCOMING TRANSMISSION

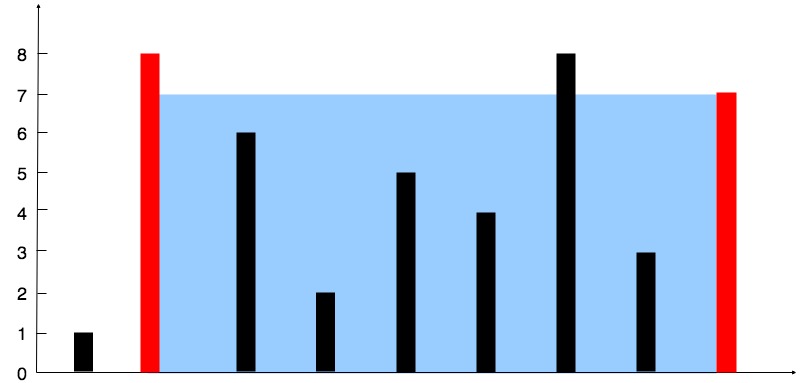
11. 盛最多水的容器 题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明： 你不能倾斜容器。 示例 1： 输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。 示例 2： 输入：height = [1,1] 输出：1 提示： n == height.length 2 <= n <= 10 5 0 <= height[i] <= 10 4 题解 在初始时，左右指针分别指向数组的左右两端，它们可以容纳的水量为 \(min(1,7)∗8=8\) 。 此时我们需要移动一个指针。移动哪一个呢？直觉告诉我们，应该移动对应数字较小的那个指针（即此时的左指针）。这是因为，由于容纳的水量是由 两个指针指向的数字中较小值∗指针之间的距离...

旋转式位置编码（ROPE） 原始的Sinusoidal位置编码总的感觉是一种“想要成为相对位置编码的绝对位置编码”。一般来说，绝对位置编码具有实现简单、计算速度快等优点，而相对位置编码则直接地体现了相对位置信号，跟我们的直观理解吻合，实际性能往往也更好。由此可见，如果可以通过绝对位置编码的方式实现相对位置编码，那么就是“集各家之所长”、“鱼与熊掌兼得”了。Sinusoidal位置编码隐约做到了这一点，但并不够好。 本文将会介绍我们自研的Rotary Transformer（RoFormer）模型，它的主要改动是应用了笔者构思的“旋转式位置编码（Rotary Position Embedding，RoPE）”，这是一种配合Attention机制能达到“绝对位置编码的方式实现相对位置编码”的设计。而也正因为这种设计，它还是目前唯一一种可用于线性Attention的相对位置编码。 RoFormer：https://github.com/ZhuiyiTechnology/roformer 基本思路 这里简要介绍过RoPE： Transformer位置编码...

不同于RNN、CNN等模型，对于Transformer模型来说，位置编码的加入是必不可少的，因为纯粹的Attention模块是无法捕捉输入顺序的，即无法区分不同位置的Token。为此我们大体有两个选择： 想办法将位置信息融入到输入中，这构成了绝对位置编码的一般做法； 想办法微调一下Attention结构，使得它有能力分辨不同位置的Token，这构成了相对位置编码的一般做法。 虽然说起来主要就是绝对位置编码和相对位置编码两大类，但每一类其实又能衍生出各种各样的变种，为此研究人员可算是煞费苦心、绞尽脑汁了，此外还有一些不按套路出牌的位置编码。本文就让我们来欣赏一下研究人员为了更好地表达位置信息所构建出来的“八仙过海，各显神通”般的编码方案。 绝对位置编码 形式上来看，绝对位置编码是相对简单的一种方案，但即便如此，也不妨碍各路研究人员的奇思妙想，也有不少的变种。一般来说，绝对位置编码会加到输入中：在输入的第 𝑘 个向量 \(𝑥_𝑘\) 中加入位置向量 \(𝑝_𝑘\) 变为 \(\boldsymbol{x}_k + \boldsymbol{p}_k\) ，其中 \(...

2022年中旬，以扩散模型为核心的图像生成模型将AI绘画带入了大众的视野。实际上，在更早的一年之前，就有了一个能根据文字生成高清图片的模型——VQGAN。VQGAN不仅本身具有强大的图像生成能力，更是传承了前作VQVAE把图像压缩成离散编码的思想，推广了「先压缩，再生成」的两阶段图像生成思路，启发了无数后续工作。 VQGAN 核心思想 VQGAN的论文名为 Taming Transformers for High-Resolution Image Synthesis，直译过来是「驯服Transformer模型以实现高清图像合成」。可以看出，该方法是在用Transformer生成图像。可是，为什么这个模型叫做VQGAN，是一个GAN呢？这是因为，VQGAN使用了两阶段的图像生成方法： 训练时，先训练一个图像压缩模型（包括编码器和解码器两个子模型），再训练一个生成压缩图像的模型。 生成时， 先用第二个模型生成出一个压缩图像，再用第一个模型复原成真实图像 。 其中，第一个图像压缩模型叫做VQGAN，第二个压缩图像生成模型是一个基于Transformer的模型。...

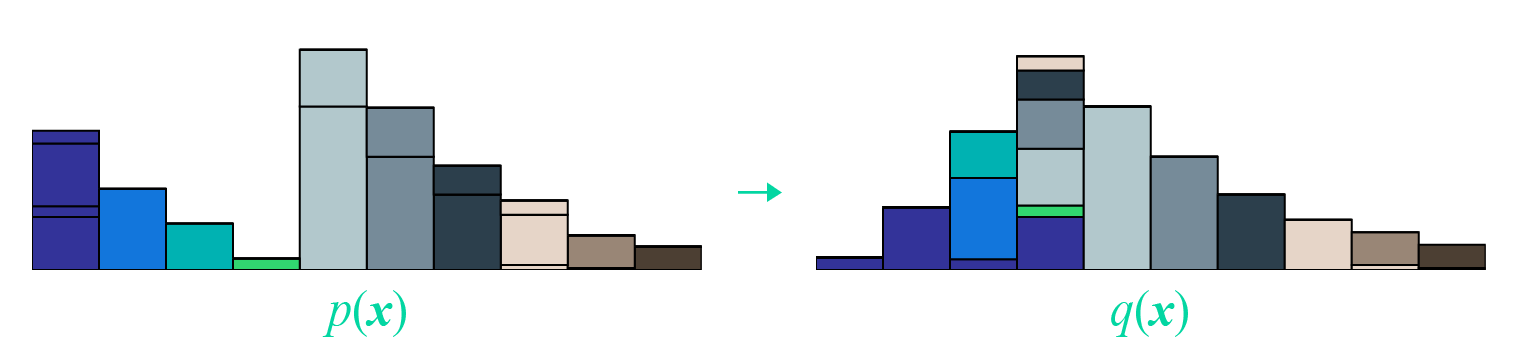
本文受启发于著名的国外博文 《Wasserstein GAN and the Kantorovich-Rubinstein Duality》 ，内容跟它大体上相同，但是删除了一些冗余的部分，对不够充分或者含糊不清的地方作了补充。 Wasserstein距离 显然，整篇文章必然围绕着Wasserstein距离（ \(\mathcal{W}\) 距离）来展开。假设我们有了两个概率分布 \(p(x),q(x)\) ，那么Wasserstein距离的定义为 \[\mathcal{W}[p,q]=\inf_{\gamma\in \Pi[p,q]} \iint \gamma(\boldsymbol{x},\boldsymbol{y}) d(\boldsymbol{x},\boldsymbol{y}) d\boldsymbol{x}d\boldsymbol{y}\] 事实上，这也算是最优传输理论中最核心的定义了。 成本函数 首先 \(d(x,y)\) ，它不一定是距离，其准确含义应该是一个成本函数，代表着从 \(x\) 运输到 \(y\) 的成本。常用的 \(d\) 是基于 \(l\)...

简介 生成对抗网络 ( Generative Adversarial Network, GAN ) 是由 Goodfellow 于 2014 年提出的一种对抗网络。这个网络框架包含两个部分，一个生成模型 (generative model) 和一个判别模型 (discriminative model)。其中，生成模型可以理解为一个伪造者，试图通过构造假的数据骗过判别模型的甄别；判别模型可以理解为一个警察，尽可能甄别数据是来自于真实样本还是伪造者构造的假数据。两个模型都通过不断的学习提高自己的能力，即生成模型希望生成更真的假数据骗过判别模型，而判别模型希望能学习如何更准确的识别生成模型的假数据。 网络框架 GAN 由两部分构成，一个 生成器 ( Generator ) 和一个 判别器 ( Discriminator )。对于生成器，我们需要学习关于数据 \(x\) 的一个分布 \(p_g\) ，首先定义一个输入数据的先验分布 \(p_z(z)\) ，其次定义一个映射 \(G \left(\boldsymbol{z}; \theta_g\right): \boldsymbol{z}...