状态价值(State values)
定义
状态价值是强化学习中的核心概念,用于衡量Agent从某个状态出发、遵循特定策略后所能获得的期望回报。
数学表达为:
其中:
- :状态 的状态价值函数(state-value function) 或者简称为 状态价值(state value);
- :智能体遵循的策略;
- :从当前时间步 开始的折扣回报;
- :折扣因子,用于平衡即时奖励和未来奖励。
状态价值的特点
- **依赖于状态 **:状态价值是条件期望,条件是智能体从状态 开始。
- **依赖于策略 **:不同策略会生成不同的轨迹,从而影响状态价值。
- 与时间步无关:状态价值是一个固定值,与当前时间步 无关。
- 代表一个状态的价值。如果一个状态的价值更高,那么策略就更好,因为可以获得更大的累积奖励。
💡 **Return和State value的区别:return是一个轨迹带来的折扣奖励和,而state value 是在一个policy下所有的轨迹奖励和的期望也就是所有轨迹对应的return的期望**
贝尔曼方程(Bellman Equation)
定义与核心思想
贝尔曼方程是一组线性方程,描述了所有状态价值之间的相互关系。通过求解贝尔曼方程,可以计算出所有状态的价值,从而实现策略评估(Policy Evaluation)
贝尔曼方程的基础形式为:
其中:
- :从状态 出发时获得的即时奖励;
- :下一时间步的状态;
- :对未来回报的折扣期望。
推导过程
通过分解回报 的形式:
带入 1式 可以得到:
进一步分解为:
可以看出上式存在两个部分,将在下面具体展开:
First term: 即时奖励期望
首先, 计算第一项 :
其中, 依赖于 。
🧾 给定事件 ,证明相当简单。
Second term:未来(折扣)回报期望
首先,我们计算未来奖励的均值,
然后我们将其与折扣因子 相乘。为了简单起见,我们说第二个项 是“未来奖励的平均值”,它是折扣的。
🧾 上面推导过程中,第一行也来自 全期望值定理;
合并到一起
将上面两个项合在一起就得到了贝尔曼方程的完整形式:
- 贝尔曼方程是一组线性方程,描述了所有状态值之间的关系。
- 上述逐元素形式对每个状态 ** 都有效。这意味着有 个这样的方程!**
- 和 ** 代表系统模型**
Examples
还是以Grid-World为例。
确定性策略
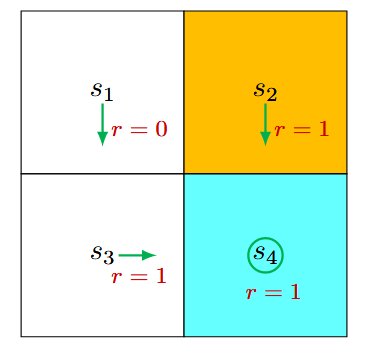
首先,考虑状态 。在该策略下,采取行动的概率为
状态转移概率为
奖励概率是:
将这些值代入之前提到的贝尔曼方程 式2 中,得到:
同理, 可以得到
我们可以从这些方程中求解状态值。由于方程简单,我们可以手动求解。更复杂的方程可以通过后面提出的算法求解。在这里,状态值可以求解为
如果设置 , 则
随机策略
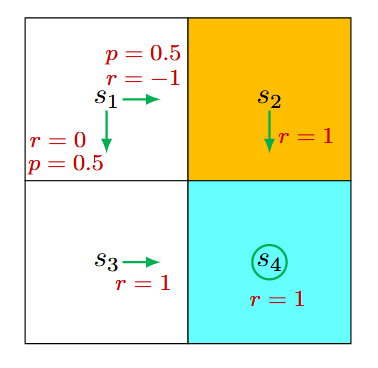
在状态 ,向右和向下的概率均为 0.5。从数学上讲,我们有 和 。状态转移概率是确定的,因为 和 。奖励概率也是确定的,因为 和 。将这些值代入 式2 得到
同样,可以得到
同样可以手动求解出上面方程组,得到
设置 , 则
这表明第一个例子的策略更好,因为它具有更大的状态值。 这个数学结论与直觉是一致的,即第一个策略更好,因为当Agent从 移动时,它可以避免进入禁区。结论是,以上两个示例表明状态值可用于评估策略。
贝尔曼方程的计算方法
式2 中的贝尔曼方程是一种 element-wise的形式, 这意味着有像这样的 个方程!如果我们把所有方程放在一起,我们得到一组线性方程,可以简洁地写成矩阵-向量 的形式。
矩阵-向量形式
首先, 我们对 式2 进行重写,
其中,
假设状态可以按 索引。对于状态 ,对应的贝尔曼方程是
将所有这些状态方程合并并重写为矩阵-向量形式
其中:
- :状态价值向量;
- :即时奖励向量;
- :状态转移概率矩阵。
通过矩阵形式,可以更直观地理解状态间的依赖关系,并为求解提供便利。
矩阵-向量形式的解
闭式解法
利用矩阵求逆,直接求解:
特点: