Batch Normalization

什么是批归一化（Batch Normalization）

以前在神经网络训练中，只是对输入层数据进行归一化处理，却没有在中间层进行归一化处理。要知道，虽然我们对输入数据进行了归一化处理，但是输入数据经过 $\sigma(WX+b)$这样的矩阵乘法以及非线性运算之后，其数据分布很可能被改变，而随着深度网络的多层运算之后，数据分布的变化将越来越大。如果我们能在网络的中间也进行归一化处理，是否对网络的训练起到改进作用呢？答案是肯定的。

这种在神经网络中间层也进行归一化处理，使训练效果更好的方法，就是批归一化Batch Normalization（BN）。

其作用在整个mini-batch上，沿着C维度对N,H,W三个维度进行归一化。具体来说，就是把第1个样本的第1个通道，加上第2个样本第1个通道 ...... 加上第 N 个样本第1个通道，求平均，得到通道 1 的均值（注意是除以 N×H×W 而不是单纯除以 N，最后得到的是一个代表这个 batch 第1个通道平均值的数字，而不是一个 H×W 的矩阵）。求通道 1 的方差也是同理。对所有通道都施加一遍这个操作，就得到了所有通道的均值和方差。

# coding;utf8
import torch
from torch import nn

# track_running_stats=False，求当前 batch 真实平均值和标准差，
# s
# affine=False, 只做归一化，不乘以 gamma 加 beta（通过训练才能确定）
# num_features 为 feature map 的 channel 数目
# eps 设为 0，让官方代码和我们自己的代码结果尽量接近

bn = nn.BatchNorm2d(num_features=3, eps=0, affine=False, track_running_stats=False)

x = torch.randn(10, 3, 5, 5)*10000 #x.shape:[10,3,5,5]
official_bn = bn(x)

# 把 channel 维度单独提出来，而把其它需要求均值和标准差的维度融合到一起

# x.permute(1, 0, 2, 3).shape: [c,n,h,w]
# x.permute(1, 0, 2, 3).contiguous(): [c,n,h,w]
# x.permute(1, 0, 2, 3).contiguous().view(3, -1): [c, n x h x w]

# x1 = x.permute(1, 0, 2, 3).contiguous().view(3, -1)
x1 = x.transpose(0,1).contiguous().view(3,-1)

# x1.mean(dim=1).shape: [3]
mu = x1.mean(dim=1).view(1, 3, 1, 1)

# unbiased=False, 求方差时不做无偏估计（除以 N-1 而不是 N），和原始论文一致 unbiased = False
# x1.std(dim=1).shape: [3]
std = x1.std(dim=1, unbiased=False).view(1, 3, 1, 1)
my_bn = (x - mu)/std

diff = (official_bn - my_bn).sum()
print(my_bn)

print('diff={}'.format(diff))

如何理解 Internal Covariate Shift？

深度神经网络模型的训练为什么会很困难？其中一个重要的原因是，深度神经网络涉及到很多层的叠加，而每一层的参数更新会导致上层的输入数据分布发生变化，通过层层叠加，高层的输入分布变化会非常剧烈，这就使得高层需要不断去重新适应底层的参数更新。为了训好模型，我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。

Google 将这一现象总结为 Internal Covariate Shift，简称 ICS。什么是 ICS 呢？

大家都知道在统计机器学习中的一个经典假设是“源空间（source domain）和目标空间（target domain）的数据分布（distribution）是一致的”。如果不一致，那么就出现了新的机器学习问题，如 transfer learning / domain adaptation 等。而 covariate shift 就是分布不一致假设之下的一个分支问题，它是指源空间和目标空间的条件概率是一致的，但是其边缘概率不同。

大家细想便会发现，的确，对于神经网络的各层输出，由于它们经过了层内操作作用，其分布显然与各层对应的输入信号分布不同，而且差异会随着网络深度增大而增大，可是它们所能“指示”的样本标记（label）仍然是不变的，这便符合了covariate shift的定义。由于是对层间信号的分析，也即是“internal”的来由。

那么ICS会导致什么问题？

简而言之，每个神经元的输入数据不再是“独立同分布”。

其一，上层参数需要不断适应新的输入数据分布，降低学习速度。

其二，下层输入的变化可能趋向于变大或者变小，导致上层落入饱和区，使得学习过早停止。

其三，每层的更新都会影响到其它层，因此每层的参数更新策略需要尽可能的谨慎。

批归一化（BN）算法的优点

下面我们来说一下BN算法的优点：

减少了人为选择参数。在某些情况下可以取消 dropout 和 L2 正则项参数,或者采取更小的 L2 正则项约束参数；
减少了对学习率的要求。现在我们可以使用初始很大的学习率或者选择了较小的学习率，算法也能够快速训练收敛；
可以不再使用局部响应归一化。BN 本身就是归一化网络(局部响应归一化在 AlexNet 网络中存在)
破坏原来的数据分布，一定程度上缓解过拟合（防止每批训练中某一个样本经常被挑选到，文献说这个可以提高 1% 的精度）。
减少梯度消失，加快收敛速度，提高训练精度。

批归一化（BN）算法流程

下面给出 BN 算法在训练时的过程

输入：上一层输出结果$X = {x_1, x_2, ..., x_m}$ ，学习参数$ \gamma, \beta $

算法流程：

计算上一层输出数据的均值 $ \mu_{\beta} = \frac{1}{m} \sum_{i=1}^m(x_i)$，其中， $m$ 是此次训练样本 batch 的大小。
计算上一层输出数据的标准差$ \sigma_{\beta}^2 = \frac{1}{m} \sum_{i=1}^m (x_i - \mu_{\beta})^2 $
归一化处理, 得到$ \hat x_i = \frac{x_i + \mu_{\beta}}{\sqrt{\sigma_{\beta}^2} + \epsilon} $，其中 $ \epsilon $ 是为了避免分母为 0 而加进去的接近于 0 的很小值
重构，对经过上面归一化处理得到的数据进行重构，得到$ y_i = \gamma \hat x_i + \beta $：，其中$ \gamma, \beta $，为可学习参数。
注：上述是 BN 训练时的过程，但是当在测试时，往往只是输入一个样本，没有所谓的均值 $ \mu_{\beta} $和标准差 $ \sigma_{\beta}^2 $。此时，均值 $ \mu_{\beta} $ 是计算所有 batch $ \mu_{\beta} $值的平均值得到，标准差 $ \sigma_{\beta}^2 $采用每个batch $ \sigma_{\beta}^2 $的无偏估计得到。

Batch Normalization在什么时候用比较合适？

在CNN中，BN应作用在非线性映射前。在神经网络训练时遇到收敛速度很慢，或梯度爆炸等无法训练的状况时可以尝试BN来解决。另外，在一般使用情况下也可以加入BN来加快训练速度，提高模型精度。

BN比较适用的场景是：每个mini-batch比较大，数据分布比较接近。在进行训练之前，要做好充分的shuffle，否则效果会差很多。另外，由于BN需要在运行过程中统计每个mini-batch的一阶统计量和二阶统计量，因此不适用于动态的网络结构和RNN网络。

Layer Normalization

Batch Normalization 的一个缺点是需要较大的 batchsize 才能合理估训练数据的均值和方差(横向计算)，这导致内存很可能不够用，同时它也很难应用在训练数据长度不同的 RNN 模型上。Layer Normalization (LN) 的一个优势是不需要批训练，在单条数据内部就能归一化。

LN不再对mini-batch中的所有特征计算均值和方差，而是沿着batch维度对CHW三个维度进行归一化操作，从而克服了BN操作对于batch size大小比较敏感的缺点，非常适用于RNN网络的加速训练。

# coding;utf8
import torch
from torch import nn

x = torch.randn(10, 3, 5, 5)*10000 #x.shape:[10,3,5,5]

# normalization_shape 相当于告诉程序这本书有多少页，每页多少行多少列
# eps=0 排除干扰
# elementwise_affine=False 不作映射
# 这里的映射和 BN 以及下文的 IN 有区别，它是 elementwise 的 affine，
# 即 gamma 和 beta 不是 channel 维的向量，而是维度等于 normalized_shape 的矩阵
ln = nn.LayerNorm(normalized_shape=[3,5,5], eps=0, elementwise_affine = False)

official_ln = ln(x)

# 把 channel 维度单独提出来，而把其它需要求均值和标准差的维度融合到一起
x1 = x.contiguous().view(10, -1)

# x1.mean(dim=1).shape: [10]
mu = x1.mean(dim=1).view(10, 1, 1, 1)

# unbiased=False, 求方差时不做无偏估计（除以 N-1 而不是 N），和原始论文一致 unbiased = False
# x1.std(dim=1).shape: [3]
std = x1.std(dim=1, unbiased=False).view(10, 1, 1, 1)
my_ln = (x - mu)/std

diff = (official_ln - my_ln).sum()
print(my_ln)

print('diff={}'.format(diff))

Instance Normalization

Instance Normalization (IN) 最初用于图像的风格迁移。作者发现，在生成模型中， feature map 的各个 channel 的均值和方差会影响到最终生成图像的风格，因此可以先把图像在 channel 层面归一化，然后再用目标风格图片对应 channel 的均值和标准差“去归一化”，以期获得目标图片的风格。

IN 操作也在单个样本内部进行，不依赖 batch。

对于$x\in \mathcal{R}^{N\times C\times H\times W}$，IN 对每个样本的 H、W 维度的数据求均值和标准差，保留 N 、C 维度，也就是说，它只在 channel 内部求均值和标准差.

import torch
from torch import nn


x = torch.rand(10, 3, 5, 5) * 10000

# track_running_stats=False，求当前 batch 真实平均值和标准差，
# 而不是更新全局平均值和标准差
# affine=False, 只做归一化，不乘以 gamma 加 beta（通过训练才能确定）
# num_features 为 feature map 的 channel 数目
# eps 设为 0，让官方代码和我们自己的代码结果尽量接近

In = nn.InstanceNorm2d(num_features=3, eps=0, affine=False, track_running_stats=False)

offcial_in = In(x)

x1 = x.view(30, -1)
mu = x1.mean(dim=1).view(10, 3, 1, 1)
std = x1.std(dim=1, unbiased=False).view(10, 3, 1, 1)

my_in = (x - mu)/std

diff = (my_in - offcial_in).sum()
print('diff={}'.format(diff))

Group Normalization

Group Normalization (GN) 适用于占用显存比较大的任务，例如图像分割。对这类任务，可能 batchsize 只能是个位数，再大显存就不够用了。而当 batchsize 是个位数时，BN 的表现很差，因为没办法通过几个样本的数据量，来近似总体的均值和标准差。GN 也是独立于 batch 的，它是 LN 和 IN 的折中。GN 计算均值和标准差时，把每一个样本 feature map 的 channel 分成 G 组，每组将有 C/G 个 channel，然后将这些 channel 中的元素求均值和标准差。各组 channel 用其对应的归一化参数独立地归一化。

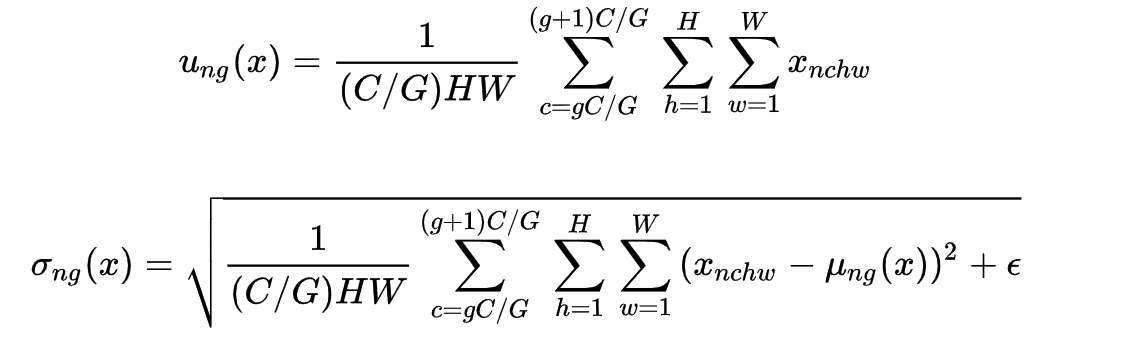
import torch
from torch import nn


x = torch.rand(10, 20, 5, 5)*10000
# 分成 4 个 group
gn = nn.GroupNorm(num_groups=4, num_channels=20, eps=0, affine=False)
official_gn = gn(x)

#把同一个group的元素融合到一起
# 分成 4 个 group

x1 = x.view(10, 4, -1)
mu = x1.mean(dim=-1).reshape(10, 4, -1)
std = x1.std(dim=-1).reshape(10, 4, -1)

x1_norm = (x1 - mu)/std
my_gn = x1_norm.reshape(10, 20, 5, 5)

diff = (my_gn - official_gn).sum()

print('diff={}'.format(diff))

RMSNorm

文章指出，尽管 LayerNorm 带来了训练稳定性和速度的提升，但它也引入了额外的计算开销：

计算开销问题：
效率权衡：

Layer Normalization计算效率低

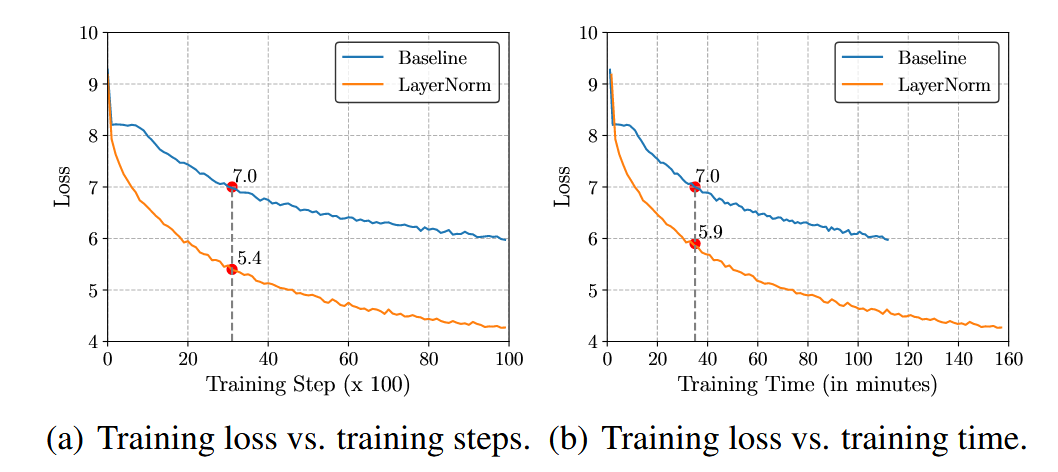
RMSNorm主要面向Layer Norm改进，归一化可以实现张量的聚集(re-centering)和缩放(re-scaling)，在RNN等变长序列处理上，L-N的计算与批次解耦，使模型能够更多的学习序列转化关系，B-N则会受到不同输入的影响，模型无法专注于序列转化。但L-N在计算成本和耗时上比较昂贵，如图1中，当基准模型的损失为7.0时，花费相同的步数和相同时间的L-N模型的损失是有差异的，相同时间(b)的损失为5.9，高于相同步数(a)的损失5.4。

RMSNorm

L-N可以通过均值 $μ$ 上的计算实现去中心，通过方差 $σ$ 上的计算实现缩放，依托于中心化，模型在输入和权重上出现噪声时依旧具有不变的分布(99个0和1个100，中心化后不会改变99个较小值与1个较大值的分布)，但文中指出L-N对张量所做的聚集中心化(re-centering)并不能够使梯度的方差减小，L-N的成功跟其关系并不大。

L-N计算

\[ {\bar{a}}_{i} = \frac{{a}_{i} - \mu }{\sigma }{g}_{i},\;{y}_{i} = f\left( {{\bar{a}}_{i} + {b}_{i}}\right) \]

L-N均值方差参数

\[ \mu = \frac{1}{n}\mathop{\sum }\limits_{{i = 1}}^{n}{a}_{i},\;\sigma = \sqrt{\frac{1}{n}\mathop{\sum }\limits_{{i = 1}}^{n}{\left( {a}_{i} - \mu \right) }^{2}} \]

RMSNorm舍弃了中心化操作，归一化过程只实现缩放，缩放系数是均方根(RMS)，L-N的均值 $μ$ 为0时便是RMSNorm，RMS所做的只是缩放，不会改变数据原本的分布，有利于激活函数输出的稳定（缩放不改变向量方向）：

\[ {\bar{a}}_{i} = \frac{{a}_{i}}{\operatorname{RMS}\left( \mathbf{a}\right)}{g}_{i}\;\;\; \text{where}\operatorname{RMS}\left( \mathbf{a}\right) = \sqrt{\frac{1}{n}\mathop{\sum }\limits_{{i = 1}}^{n}{a}_{i}^{2}} \]

恒定&梯度(Invariance&Gradient Analysis)

不变性：

考虑输入和权重变化时，不同标准化因为采用方式不同，在不变性上的表现也有差异：

考虑以下RMSNorm一般形式：

\[ \mathbf{y} = f\left( {\frac{\mathbf{{Wx}}}{\operatorname{RMS}\left( \mathbf{a}\right) } \odot \mathbf{g} + \mathbf{b}}\right) , \]

其中，$x$ 是输入向量， $W$ 是权重矩阵：

RMSNorm 对权重矩阵和输入重新缩放都是不变的，因为 RMS 具有以下线性特性：

\[ \operatorname{RMS}\left( {\alpha \mathbf{x}}\right) = \alpha \operatorname{RMS}\left( \mathbf{x}\right) , \]

其中， $\alpha$是缩放因子，假设权重矩阵按 $δ$ 因子缩放( $W^′=δW $)，输出不会受到影响：

\[ {\mathbf{y}}^{\prime } = f\left( {\frac{{\mathbf{W}}^{\prime }\mathbf{x}}{\operatorname{RMS}\left( {\mathbf{a}}^{\prime }\right) } \odot \mathbf{g} + \mathbf{b}}\right) = f\left( {\frac{\delta \mathbf{W}\mathbf{x}}{\delta \operatorname{RMS}\left( \mathbf{a}\right) } \odot \mathbf{g} + \mathbf{b}}\right) = \mathbf{y}. \]

梯度:

现有大多数神经网络的学习过程，都依赖基于梯度的方向传播来实现参数更新，因此梯度求解的鲁棒性是模型参数更新及收敛的重要依靠，从这一视角看归一化方法的成功不仅仅是增强了输入的稳定性，还来源于增加了优化空间的平滑度。

给定损失函数$\mathcal{L}$，对于 $\mathbf{b}$ 和 $\mathbf{g}$ 的梯度有

\[ \frac{\partial \mathcal{L}}{\partial \mathbf{b}} = \frac{\partial \mathcal{L}}{\partial \mathbf{v}},\;\frac{\partial \mathcal{L}}{\partial \mathbf{g}} = \frac{\partial \mathcal{L}}{\partial \mathbf{v}} \odot \frac{\mathbf{{Wx}}}{\operatorname{RMS}\left( \mathbf{a}\right) }, \]

其中 $\mathbf{v}$ 代表 RMSNomr 中的 $f(⋅)$ ，

$\mathbf{g}$ 的梯度与RMS求和成比例，而不是直接与输入成比例，起到了平滑作用。对于权重 $\mathbf{W}$ :

\[ \frac{\partial \mathcal{L}}{\partial \mathbf{W}} = \mathop{\sum }\limits_{{i = 1}}^{n}{\left\lbrack {\mathbf{x}}^{T} \otimes \left( \operatorname{diag}\left( \mathbf{g} \odot \frac{\partial \mathcal{L}}{\partial \mathbf{v}}\right) \times \mathbf{R}\right) \right\rbrack }_{i}\\\text{where}\ \mathbf{R} = \frac{1}{\operatorname{RMS}\left( \mathbf{a}\right) }\left( {\mathbf{I} - \frac{\left( {\mathbf{W}\mathbf{x}}\right) {\left( \mathbf{W}\mathbf{x}\right) }^{T}}{n\operatorname{RMS}{\left( \mathbf{a}\right) }^{2}}}\right) \]

缩放 $δ$ 作用在 $\mathbf{R}$ ：

\[ {\mathbf{R}}^{\prime } = \frac{1}{\delta \operatorname{RMS}\left( \mathbf{a}\right) }\left( {\mathbf{I} - \frac{\left( {\delta \mathbf{W}\mathbf{x}}\right) {\left( \delta \mathbf{W}\mathbf{x}\right) }^{T}}{n{\delta }^{2}\operatorname{RMS}{\left( \mathbf{a}\right) }^{2}}}\right) = \frac{1}{\delta }\mathbf{R}. \]

由 ${\mathbf{R}}^{\prime } = \frac{1}{\delta }\mathbf{R}.$ ，权重矩阵的梯度与权重矩阵缩放程度负相关，从而减少梯度更新对于缩放程度的灵敏性，保证更新的平滑性和稳定性。

pRMSNorm

RMS具有线性特征，所以提出可以用部分数据的RMSNorm来代替全部的计算，pRMSNorm表示使用前p%的数据计算RMS值。$k=n*p$ 表示用于RMS计算的元素个数。实测中，使用6.25%的数据量可以收敛

\[ \bar{\operatorname{RMS}\left( \mathbf{a}\right)} = \sqrt{\frac{1}{k}\mathop{\sum }\limits_{{k = 1}}^{k}{a}_{i}^{2}} \]

class RMSNorm(torch.nn.Module):

    def __init__(
        self,
        dim: int,
        eps: float = 1e-6,
        add_unit_offset: bool = True,
    ):
        super().__init__()
        self.eps = eps
        self.add_unit_offset = add_unit_offset
        self.weight = nn.Parameter(torch.zeros(dim))

    def _norm(self, x):
        return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)

    def forward(self, x):
        x = self._norm(x.float()).type_as(x)
        if self.add_unit_offset:
            output = x * (1 + self.weight)
        else:
            output = x * self.weight
        return output