48. 旋转图像
题目
给定一个 \(n × n\) 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
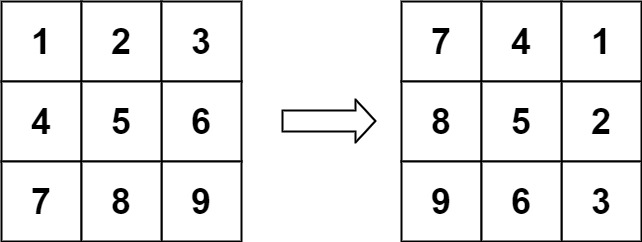
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]示例 2:
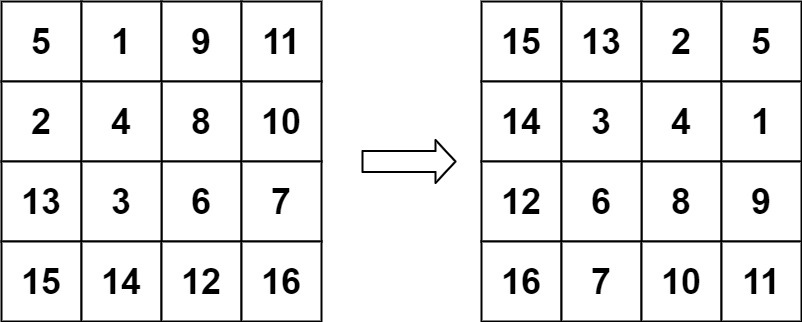
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
题解
这是一个经典的矩阵操作问题。要在原地(In-place)将图像顺时针旋转 90 度,我们可以利用矩阵的几何性质。
最直观且易于实现的方法是将旋转操作分解为两个简单的数学变换步骤:转置(Transpose)和 水平翻转(Horizontal Reflection)。
数学推导
假设我们有一个 \(n \times n\) 的矩阵,对于任意坐标\( (i, j)\) 的元素,顺时针旋转 90 度后的目标位置是 \((j, n-1-i)\)。
我们可以通过以下两步达到这个目标:
- 转置矩阵:将矩阵的行列互换。
- 翻转每一行:将每一行内的元素左右对称交换。
最终变换结果为 \((i, j) \rightarrow (j, n-1-i)\),正是顺时针旋转 90 度的映射关系。
class Solution:
def rotate(self, matrix: list[list[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
n = len(matrix)
# 1. Transpose the matrix
# 我们只需要遍历上三角矩阵(不包含对角线)进行交换即可
for i in range(n):
for j in range(i + 1, n):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
# 2. Reverse each row
# 直接使用双指针或Python内置方法反转每一行
for i in range(n):
matrix[i].reverse()
复杂度分析
- 时间复杂度: \(O(N^2)\)。我们需要遍历矩阵中的每个元素两次(一次转置,一次翻转)。
- 空间复杂度: \(O(1)\)。我们在原地修改矩阵,只使用了常数级的额外空间用于临时变量交换。
替代方法:分层旋转 (Layer-by-Layer)
如果你不想使用两次变换,也可以直接进行四角交换。这种方法是从外向内一层层旋转。
对于每一层,我们将四个相关的点进行循环交换:
- Top-Left
- Top-Right
- Bottom-Right
- Bottom-Left
交换逻辑如下:
这种方法虽然也是 \(O(1)\) 空间,但代码编写时下标容易出错,通常推荐第一种“转置+翻转”的方法。
几何概型
题目
一个绳子随机剪成三段,求能让这三段组成三角形的概率
题解:
使用“段长法”,设 \(x, y\)为其中两段绳子的长度

这张图中:
- \(x\)轴:代表第一段绳子的长度。
- \(y\)轴:代表第二段绳子的长度。
- \(L\):代表绳子的总长度。
那么第三段绳子的长度就是 \(L - x - y\)。
因为三段长度之和必须等于 \(L\),且每段长度必须大于 \(0\),所以:
构成三角形的条件
为了能围成三角形,任意一段的长度都不能超过总长度的一半(\(L/2\))。
我们需要同时满足以下三个条件:
1. 第一段不超长:\(x < L/2\)
2. 第二段不超长:\(y < L/2\)
3. 第三段不超长:\(L - x - y < L/2 \implies x + y > L/2\)
现在我们把这三个条件映射到图上,大三角形被\(x=L/2\), \(y=L/2\), \(x+y=L/2\) 这几条线分割成了4个全等的小三角形:
所以概率是:
拿球最大概率
题目
50个红球与50个白球,放入两个盒子,要求每个盒子至少有一个球。拿的时候随机在其中一个盒子内,随机拿出一个球。请问如何摆放这些球,让拿出的是红球的概率最大
题解
最佳摆放方案是:
- 盒子 A:放入 1 个红球。
- 盒子 B:放入剩下的 49 个红球 和 50 个白球。
为什么这样做?(数学推导)
我们要计算拿到红球的总概率 \(P(\text{红})\)。公式如下:
因为选盒子的概率是随机的,所以 \(P(\text{选盒子A}) = P(\text{选盒子B}) = 0.5\)。
为了让总概率最大,我们需要尽可能让 \(P(\text{红}|\text{A})\)和\(P(\text{红}|\text{B})\)都变大,或者让其中一个变成 1(100%),同时尽量不拖累另一个。
方案计算:
1. 盒子 A:只有 1 个红球。
- 拿到红球的概率是 100\%。
2. 盒子 B:有 49 个红球 + 50 个白球(共 99 个球)。
- 拿到红球的概率是 \(\frac{49}{99} \approx 0.495\)。
最终总概率:
直观理解
如果你把红球和白球均匀混合(比如每个盒子 25红+25白),你拿到红球的概率只有 50%。
通过把 1 个红球单独放在一个盒子里,你实际上是“保送”了 50% 的机会能直接拿到红球。而剩下的那个盒子,虽然白球多一点,但红球也不少(49对50),概率接近一半。
这样你就把原本 50% 的胜率提升到了将近 75%。
椭球体内接长方体的最大体积
题目
一个椭球体\((\frac{x^2}{a^2} +\frac{y^2}{b^2}+\frac{z^2}{c^2} =1)\)内接长方体的最大体积
题解
拉格朗日乘数法,
其中,\((x, y, z)\) 为内接长方体在第一象限与椭球体的交点坐标, 求解,
判断某点是否在三角形内部
题目
在2-D plane, 检查一个点是否在一个三角形内(四个点给定)
题解
- 内角和等于360°
这种方法最好理解,即对于\(△ABC\)内的某一点\(P\),连接\(PA\)、\(PB\)、\(PC\)得到三条线段,当且仅当三条线段组成的三个夹角和为360°的时候,该点才位于三角形内部。但此种方法的计算涉及到平方根、反正(余)弦,效率十分低下。
类似的还有,\(P\)与\(ABC\)三个顶点组成的三个三角形,面积之和等于\(△ABC\)的面积,同样可以证明点\(P\)位于三角形内部,但效率也很低。
- Same Side Technique
这种方法是我从别处看来的,觉得很新颖,想看英文原版的可以直接点这里。下面我解释一下该方法的思想,首先看下图:
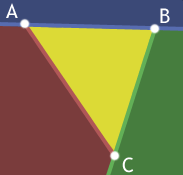
如果某点位于\(△ABC\)内部,那么该点一定位于AB的下边,AC的右边,BC的左边。要用数学的方法来表示,可以采用向量积,向量积有个很重要的右手定则。下面接着看下一张图:
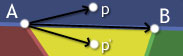
对于任意的一点P, \(\vec{AB} \times \vec{AP}\),其结果根据右手定则,应为指向屏幕外,而\(\vec{AB} \times \vec{AP^{'}}\)的结果则是指向屏幕里。根据这一特性,我们只要找到某一点\(P\),满足\(\vec{AC} \times \vec{AB}\)与\(\vec{AC} \times \vec{AP}\)具有同一方向、\(\vec{CB} \times \vec{CA}\)与\(\vec{CB} \times \vec{CP}\)具有同一方向、\(\vec{BA} \times \vec{BC}\)与\(\vec{BA} \times \vec{BP}\)具有同一方向,则点\(P\)位于\(△ABC\)内。
这种方法涉及到的计算是向量运算,没有平方根、反余弦这些,效率比第2种方法高,代码部分
class Point2D(object):
def __init__(self, x=None, y=None):
self.x = x
self.y = y
def __sub__(self, other):
res = Point2D()
res.x = self.x - other.x
res.y = self.y - other.y
return res
def cross_product_2d(a: Point2D, b: Point2D) -> float:
return a.x * b.y - a.y * b.x
def same_side(v: Point2D, v1: Point2D, v2: Point2D) -> bool:
cp1 = cross_product_2d(v, v1)
cp2 = cross_product_2d(v, v2)
return cp1 * cp2 > 0
def in_triangle(p: Point2D, a: Point2D, b: Point2D, c: Point2D) -> bool:
AB, AC, AP = b-a, c-a, p-a
BA, BC, BP = a-b, c-b, p-b
CB, CA, CP = b-c, a-c, p-c
if same_side(AC, AP, AB) and same_side(BA, BC, BP) and same_side(CB, CA, CP):
return True
else:
return False- Barycentric Coordinates
最后一种方法的效率最高,但是理解起来需要的步骤多一点,我们先看下面这张图
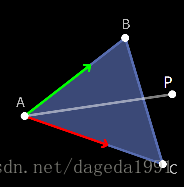
\(\vec{AP}\)可以表示为
其中\(u\)、\(v\)为常量系数,从图中我们即可得知,当\(u>0\)且\(v>0\)时,P的位置才有可能正确,那是不是\(u\)、\(v\)可以无限大呢?当然不是,当\(u+v>1\)时,\(P\)就会超出三角形的范围,而当\(u+v=1\)时,点\(P\)刚好位于\(BC\)上,这里稍微证明一下。
当点\(P\)在\(BC\)上时,也就是 \(\vec{BP},\vec{PC}\)同向,将前面 \(\vec{AP}\)的表示方式代入,那么这两个向量可以分别表示为:
由于两者同向,那么就存在一个\( λ( λ>0)\),使得\( \vec{BP}=λ\vec{PC}\),代入上面两式,整理一下,就得到了下面的式子:
上式要成立,当且仅当左右两边的系数都为0。由此得到两个方程,消去 λ就可以得到\(u+v=1\)了。有了这一点,为什么三角形内部点的\(u\)、\(v\)之和小于1,外部点的大于1,请读者自行理解,这里不再展开了。
由此我们的模型就得到了:对于任意给定的一点\(P\),判断其是否位于\(△ABC\)的内部,就是要计算其相对于\(△ABC\)的\(u\)、\(v\)值,只要这两个值满足\(u>0\)、 \(v>0\)、 \(u+v<1\),那么可以确定点P位于三角形内。这样只要得到\(u\)、\(v\)的表达式,在代码里面就能直接使用了。
// Compute vectors
v0 = C - A
v1 = B - A
v2 = P - A
// Compute dot products
dot00 = dot(v0, v0)
dot01 = dot(v0, v1)
dot02 = dot(v0, v2)
dot11 = dot(v1, v1)
dot12 = dot(v1, v2)
// Compute barycentric coordinates
invDenom = 1 / (dot00 * dot11 - dot01 * dot01)
u = (dot11 * dot02 - dot01 * dot12) * invDenom
v = (dot00 * dot12 - dot01 * dot02) * invDenom
// Check if point is in triangle
return (u >= 0) && (v >= 0) && (u + v < 1)2-D凸多边形面积
思路
可以将凸多边形(边数\(n > 3\))划分为 (\(n - 2\)) 个三角形,分别运用向量叉积计算每个三角形的面积,最后累加各个三角形的面积就是多边形的面积。
class Point(object):
def __init__(self, x, y):
self.x = x
self.y = y
# 计算三角形面积
def getS(a: Point,b:Point, c:Point) -> float:
# 应用叉积的定义推出的
area = ((b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x)) / 2
return area
#计算多边形面积。必须确保 n>=3,且多边形是凸多边形
def getPS(p:List[Point], n:int) -> float:
sumS = 0
for i in range(1, n):
#n-2个三角形的面积和
sumS += getS(p[1], p[i], p[i + 1])
return sumS圆环上随机取3个点组成一个锐角三角形的概率
题目
在一个圆环上随机取3点,求这3个点组成一个锐角三角形的概率
题解
如下图所示:
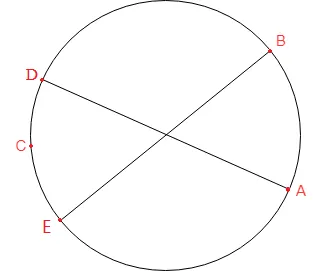
取单位圆上任意两点点\(A\)和\(B\),\(A\)、\(B\)两点确定以后,点\(A\)、\(B\)、\(C\)三点要够成锐角三角形,点\(C\)必须在\(DE\)之间,否在将构成钝角三角形。设\(AB\)弧所对应的圆心角为\(θ\),则当且仅当\(θ∈(0,π)\) 时有可能构成锐角三角形。\(θ\)的概率密度是 \(\frac{1}{π}\),此时组成锐角三角形需要C点在AB对应的DE段间的概率是 \(\frac{θ}{2π}\)。故在一个圆环上随机添加3点,三个点组成一个锐角三角形的概率为
为什么点 C 必须在 DE 之间?(几何条件)
图中 \(D\) 是 \(A\) 的对径点(直径的另一端),\(E\) 是 \(B\) 的对径点。
- 锐角三角形的充要条件是:圆周上任意两点之间的弧长都不能超过半圆(即圆心角不能超过 \(\pi\))。
- 固定 \(A\) 和 \(B\) 后,如果点 \(C\) 落在弧 \(BD\) 上,那么 \(A, B, C\) 就在以 \(AD\) 为界的半圆内,会构成钝角三角形。
- 同理,如果点 \(C\) 落在弧 \(AE\) 上,\(A, B, C\) 就在以 \(BE\) 为界的半圆内,也会构成钝角三角形。
- 结论:点 \(C\) 只有落在剩下的弧 \(DE\) 上,才能保证三个点不落在任何一个半圆内。而弧 \(DE\) 的长度(圆心角)恰好等于弧 \(AB\) 的长度(圆心角 \(\theta\))。
为什么 \(\theta\) 的概率密度是 \(\frac{1}{\pi}\) 而不是 \(\frac{1}{2\pi}\)?(概率定义)
这是一个容易产生困惑的地方。
- 如果我们把 \(B\)看作在 \(0\) 到 \(2\pi\) 上均匀分布,那么概率密度确实是 \(\frac{1}{2\pi}\)。
- 但是,题目解法中定义的 \(\theta\) 是 “AB弧所对应的圆心角”(通常指劣弧),这就限制了 \(\theta\) 的取值范围是 \(0\) 到 \(\pi\)。
- 对于任意一个确定的弧长 \(\theta\)(例如 \(30^\circ\)),点 \(B\)可以在点 \(A\)的顺时针方向,也可以在逆时针方向。也就是说,圆周上有两个位置能让 \(AB\) 的弧长等于 \(\theta\)。
因此,弧长 \(\theta\) 的分布密度就变成了 \(\frac{1}{2\pi} \times 2 = \frac{1}{\pi}\)。
#! /usr/bin/env python3
# -*- coding: utf-8 -*-
# @Author: wzdnzd
import numpy as np
def simulate(n):
# 圆心角θ所对应的弦长 l = 2 * R * sin(θ/2), R为圆的半径
def compute(theta):
if theta > np.pi:
theta = 2 * np.pi - theta
return 2 * np.sin(theta / 2)
# 根据三角形三条边的平方关系判断是否是锐角、直角或钝角三角形
def judge(array):
if len(array) != 3:
raise ValueError('len(array) must be 3.')
if array[0] ** 2 + array[1] ** 2 > array[2] ** 2:
return -1
elif array[0] ** 2 + array[1] ** 2 == array[2] ** 2:
return 0
else:
return 1
acute, right, obtuse = 0, 0, 0
for _ in range(n):
angles = sorted(np.random.rand(3) * 2 * np.pi)
chords = sorted([compute(angles[1] - angles[0]),
compute(angles[2] - angles[1]),
compute(2 * np.pi + angles[0] - angles[2])])
flag = judge(chords)
if flag == -1:
acute += 1
elif flag == 0:
right += 1
else:
obtuse += 1
return [x / n for x in [acute, right, obtuse]]
if __name__ == "__main__":
probabilities = simulate(100000)
print('acute: {}\tright: {}\tobtuse: {}'.format(
probabilities[0], probabilities[1], probabilities[2]))运行结果如下:
acute: 0.25044 right: 0.0 obtuse: 0.74956