RNN

概述

在前面讲到的DNN和CNN中，训练样本的输入和输出是比较的确定的。但是有一类问题DNN和CNN不好解决，就是训练样本输入是连续的序列,且序列的长短不一，比如基于时间的序列：一段段连续的语音，一段段连续的手写文字。这些序列比较长，且长度不一，比较难直接的拆分成一个个独立的样本来通过DNN/CNN进行训练。

而对于这类问题，RNN则比较的擅长。那么RNN是怎么做到的呢？RNN假设我们的样本是基于序列的。比如是从序列索引1到序列索引$\tau$ 。对于这其中的任意序列索引号 $t$,它对应的输入是对应的样本序列中的 $x(t)$。而模型在序列索引号 $t$ 位置的隐藏状态 $h(t)$，则由$x(t)$和在$t-1$位置的隐藏状态$h(t-1)$共同决定。在任意序列索引号 $t$，我们也有对应的模型预测输出 $o(t)$。通过预测输出 $o(t)$和训练序列真实输出 $y(t)$,以及损失函数 $L(t)$，我们就可以用DNN类似的方法来训练模型，接着用来预测测试序列中的一些位置的输出。

下面我们来看看RNN的模型。

模型

RNN模型有比较多的变种，这里介绍最主流的RNN模型结构如下：

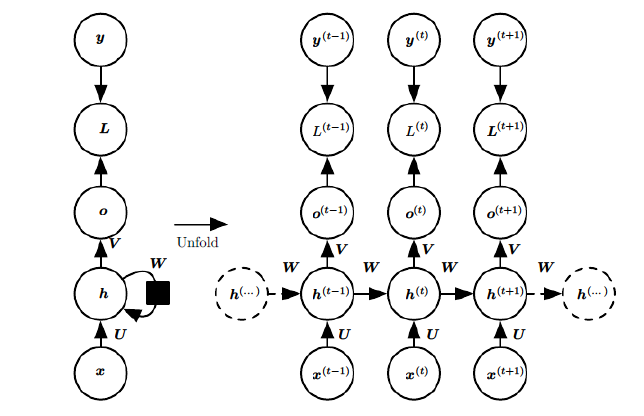
上图中左边是RNN模型没有按时间展开的图，如果按时间序列展开，则是上图中的右边部分。我们重点观察右边部分的图。

这幅图描述了在序列索引号 $t$ 附近RNN的模型。其中：

1）$x(t)$ 代表在序列索引号$t$时训练样本的输入。同样的，$x(t-1)$和x(t+1)代表在序列索引号$t-1$和$t+1$时训练样本的输入。

2）$h(t)$代表在序列索引号$t$时模型的隐藏状态。$h(t)$由$x(t)$和$h(t-1)$共同决定。

3）$o(t)$代表在序列索引号$t$时模型的输出。$o(t)$只由模型当前的隐藏状态$h(t)$决定。

4）$L(t)$代表在序列索引号$t$时模型的损失函数。

5）$y(t)$代表在序列索引号$t$时训练样本序列的真实输出。

6）$U,W,V$这三个矩阵是我们的模型的线性关系参数，它在整个RNN网络中是共享的，这点和DNN很不相同。 也正因为是共享了，它体现了RNN的模型的“循环反馈”的思想。

前向传播算法

有了上面的模型，RNN的前向传播算法就很容易得到了。

对于任意一个序列索引号$t$，我们隐藏状态$h(t)$由$x(t)$和$h(t-1)$得到：

其中 $\sigma$ 为RNN的激活函数，一般为$tanh$, $b$为线性关系的偏倚。

序列索引号$t$时模型的输出$o(t)$的表达式比较简单：

在最终在序列索引号$t$时我们的预测输出为:

通常由于RNN是识别类的分类模型，所以上面这个激活函数一般是softmax。

通过损失函数$L(t)$，比如对数似然损失函数，我们可以量化模型在当前位置的损失，即$\hat{y}(t)$和$y(t)$的差距。

反向传播算法推导

有了RNN前向传播算法的基础，就容易推导出RNN反向传播算法的流程了。RNN反向传播算法的思路和DNN是一样的，即通过梯度下降法一轮轮的迭代，得到合适的RNN模型参数$U,W,V,b,c$。由于我们是基于时间反向传播，所以RNN的反向传播有时也叫做BPTT(back-propagation through time)。当然这里的BPTT和DNN也有很大的不同点，即这里所有的$U,W,V,b,c$在序列的各个位置是共享的，反向传播时我们更新的是相同的参数。

为了简化描述，这里的损失函数我们为交叉熵损失函数，输出的激活函数为softmax函数，隐藏层的激活函数为tanh函数。

对于RNN，由于我们在序列的每个位置都有损失函数，因此最终的损失$L$为：

其中$V,c$ 的梯度计算是比较简单的：

但是$W,U,b$ 的梯度计算就比较的复杂了。从RNN的模型可以看出，在反向传播时，在在某一序列位置$t$的梯度损失由当前位置的输出对应的梯度损失和序列索引位置$t+1$时的梯度损失两部分共同决定。对于𝑊在某一序列位置t的梯度损失需要反向传播一步步的计算。我们定义序列索引$t$ 位置的隐藏状态的梯度为：

这样我们可以像DNN一样从${\delta }^{(t+1)}$递推${\delta }^{(t)}$ 。

对于${\delta }^{(\tau )}$，由于它的后面没有其他的序列索引了，因此有：

有了${\delta }^{(t)}$,计算$W,U,b$就容易了，这里给出$W,U,b$的梯度计算表达式：

除了梯度表达式不同，RNN的反向传播算法和DNN区别不大，因此这里就不再重复总结了。

RNN小结

上面总结了通用的RNN模型和前向反向传播算法。当然，有些RNN模型会有些不同，自然前向反向传播的公式会有些不一样，但是原理基本类似。

RNN虽然理论上可以很漂亮的解决序列数据的训练，但是它也像DNN一样有梯度消失时的问题，当序列很长的时候问题尤其严重。因此，上面的RNN模型一般不能直接用于应用领域。在语音识别，手写书别以及机器翻译等NLP领域实际应用比较广泛的是基于RNN模型的一个特例LSTM.

LSTM

从RNN到LSTM

在RNN模型里，我们讲到了RNN的结构，每个序列索引位置$t$都有一个隐藏状态$h(t)$。

如果我们略去每层都有的$o(t),L(t),y(t)$，则RNN的模型可以简化成如下图的形式：

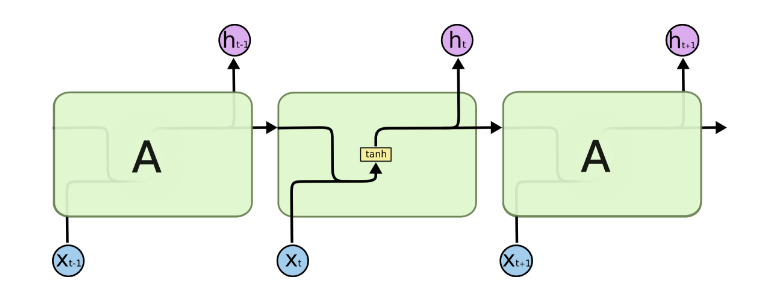
图中可以很清晰看出在隐藏状态$h(t)$由$x(t)$和$h(t-1)$得到。得到$h(t)$后一方面用于当前层的模型损失计算，另一方面用于计算下一层的$h(t+1)$。

由于RNN梯度消失的问题，大牛们对于序列索引位置$t$的隐藏结构做了改进，可以说通过一些技巧让隐藏结构复杂了起来，来避免梯度消失的问题，这样的特殊RNN就是我们的LSTM。由于LSTM有很多的变种，这里我们以最常见的LSTM为例讲述。LSTM的结构如下图：

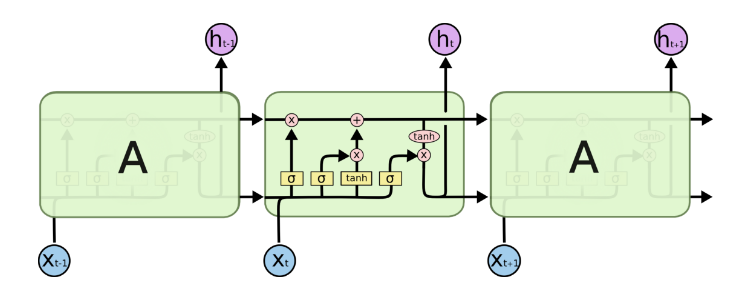
可以看到LSTM的结构要比RNN的复杂的多，真佩服牛人们怎么想出来这样的结构，然后这样居然就可以解决RNN梯度消失的问题？由于LSTM怎么可以解决梯度消失是一个比较难讲的问题，我也不是很熟悉，这里就不多说，重点回到LSTM的模型本身。

LSTM模型结构剖析

上面我们给出了LSTM的模型结构，下面我们就一点点的剖析LSTM模型在每个序列索引位置t时刻的内部结构。

从上图中可以看出，在每个序列索引位置 $t$ 时刻向前传播的除了和RNN一样的隐藏状态$h(t)$，还多了另一个隐藏状态，如图中上面的长横线。这个隐藏状态我们一般称为细胞状态(Cell State)，记为$C(t)$。如下图所示：

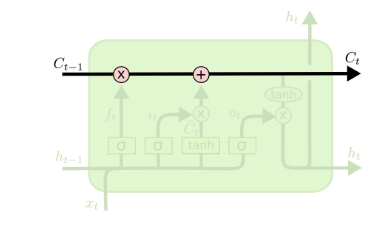
除了细胞状态，LSTM图中还有了很多奇怪的结构，这些结构一般称之为门控结构(Gate)。LSTM在在每个序列索引位置t的门一般包括遗忘门，输入门和输出门三种。下面我们就来研究上图中LSTM的遗忘门，输入门和输出门以及细胞状态。

遗忘门(forget gate)

遗忘门（forget gate）顾名思义，是控制是否遗忘的，在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。遗忘门子结构如下图所示：

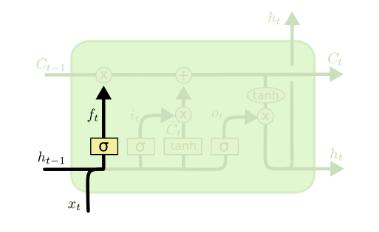
图中输入的有上一序列的隐藏状态$h(t-1)$和本序列数据$x(t)$，通过一个激活函数，一般是sigmoid，得到遗忘门的输出$f(t)$。由于sigmoid的输出$f(t)$在$[0,1]$之间，因此这里的输出$f^{(t)}$代表了遗忘上一层隐藏细胞状态的概率。用数学表达式即为：

其中$W_f,U_f,b_f$为线性关系的系数和偏倚，和RNN中的类似。$\sigma$为sigmoid激活函数。

输入门(input gate)

输入门（input gate）负责处理当前序列位置的输入，它的子结构如下图：

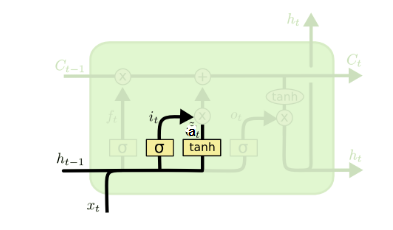
从图中可以看到输入门由两部分组成，第一部分使用了sigmoid激活函数，输出为$i(t)$,第二部分使用了$tanh$激活函数，输出为$a(t)$, 两者的结果后面会相乘再去更新细胞状态。用数学表达式即为：

其中$W_i,U_i,b_i,W_a,U_a,b_a$,为线性关系的系数和偏倚，和RNN中的类似。$\sigma$为sigmoid激活函数。

细胞状态更新(cell state)

在研究LSTM输出门之前，我们要先看看LSTM之细胞状态。前面的遗忘门和输入门的结果都会作用于细胞状态$C(t)$。我们来看看从细胞状态$C(t-1)$如何得到$C(t)$。如下图所示：

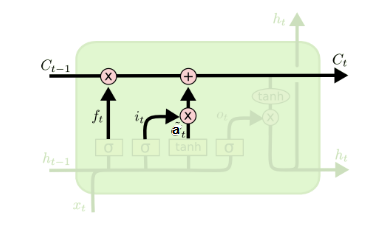
细胞状态𝐶(𝑡)由两部分组成，第一部分是$C(t-1)$和遗忘门输出$f(t)$的乘积，第二部分是输入门的$i(t)$和$a(t)$的乘积，即：

其中，$\odot$为Hadamard积(element-wise)，在DNN中也用到过。

输出门(output gate)

有了新的隐藏细胞状态$C(t)$，我们就可以来看输出门了，子结构如下：

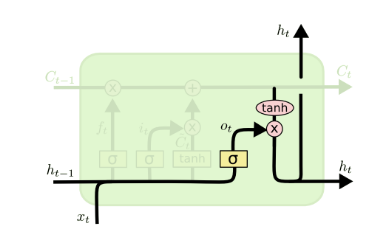
从图中可以看出，隐藏状态$h(t)$的更新由两部分组成，第一部分是$o(t)$, 它由上一序列的隐藏状态$h(t-1)$和本序列数据$x(t)$，以及激活函数sigmoid得到，第二部分由隐藏状态$C(t)$和$tanh$激活函数组成, 即：

通过本节的剖析，相信大家对于LSTM的模型结构已经有了解了。当然，有些LSTM的结构和上面的LSTM图稍有不同，但是原理是完全一样的。

前向传播算法

现在我们来总结下LSTM前向传播算法。LSTM模型有两个隐藏状态$h(t),C(t)$，模型参数几乎是RNN的4倍，因为现在多了$W_f,U_f,b_f,W_a,U_a,b_a,W_i,U_i,b_i,W_o,U_o,b_o$这些参数。

前向传播过程在每个序列索引位置的过程为：

1）更新遗忘门输出：

2）更新输入门两部分输出：

3）更新细胞状态：

4）更新输出门输出：

5）更新当前序列索引预测输出：

反向传播算法推导关键点

有了LSTM前向传播算法，推导反向传播算法就很容易了， 思路和RNN的反向传播算法思路一致，也是通过梯度下降法迭代更新我们所有的参数，关键点在于计算所有参数基于损失函数的偏导数。