softmax初探

在机器学习尤其是深度学习中，softmax是个非常常用而且比较重要的函数，尤其在多分类的场景中使用广泛。他把一些输入映射为0-1之间的实数，并且归一化保证和为1，因此多分类的概率之和也刚好为1。
首先我们简单来看看softmax是什么意思。顾名思义，softmax由两个单词组成，其中一个是max。对于max我们都很熟悉，比如有两个变量a,b。如果a>b，则max为a，反之为b。用伪码简单描述一下就是 if a > b return a; else b。
另外一个单词为soft。max存在的一个问题是什么呢？如果将max看成一个分类问题，就是非黑即白，最后的输出是一个确定的变量。更多的时候，我们希望输出的是取到某个分类的概率，或者说，我们希望分值大的那一项被经常取到，而分值较小的那一项也有一定的概率偶尔被取到，所以我们就应用到了soft的概念，即最后的输出是每个分类被取到的概率。

softmax的定义

假设有一个数组$V$，$V_i$表示$V$中的第i个元素，那么这个元素的softmax值为:

\[ S_i=\frac{e^i}{\sum_je^j} \]

该元素的softmax值，就是该元素的指数与所有元素指数和的比值。

这个定义可以说很简单，也很直观。那为什么要定义成这个形式呢？原因主要如下：
1.softmax设计的初衷，是希望特征对概率的影响是乘性的。
2.多类分类问题的目标函数常常选为cross-entropy。即$L = -\sum_k t_k \cdot lnP(y=k)$，其中目标类的$t_k$为1，其余类的$t_k$为0。在神经网络模型中(最简单的logistic regression也可看成没有隐含层的神经网络)，输出层第i个神经元的输入为$a_i = \sum_d w_{id} x_d$ 神经网络是用error back-propagation训练的，这个过程中有一个关键的量是$\partial L / \partial \alpha_i$。后面我们会进行详细推导。

softmax求导

前面提到，在多分类问题中，我们经常使用交叉熵作为损失函数

\[ Loss = - \sum_i t_i lny_i \]

其中，$t_i$表示真实值,$y_i$ 表示求出的softmax值。当预测第i个时，可以认为$t_i = 1$。此时损失函数变成了:

$$
Loss_i = -lny_i

接下来对Loss求导。根据定义：

$$
y_i = \frac{e^i}{\sum_j e^j}

我们已经将数值映射到了0-1之间，并且和为1，则有：

\[ \frac{e^i}{\sum_j e^j} = 1 - \frac{\sum_{j \neq i} e^j}{\sum_j e^j} \]

接下来开始求导

\[ \begin{aligned} \frac{\partial Loss_i}{\partial i} &= -\frac{\partial lny_i}{\partial i} \\ &= -\frac{\sum_j e^j}{e^i}\cdot \frac{\partial(\frac{e^i}{\sum_je^j})}{\partial i} \\ &= -\frac{\sum_j e^j}{e^i}\cdot (-\sum_{j \neq i} e^j)\cdot\frac{\partial(\frac{1}{\sum_je^j})}{\partial i}\\ &=\frac{\sum_je^j\cdot \sum_{j\neq i}e^j}{e^i}\cdot \frac{-e^i}{(\sum_je^j)^2}\\ &=-\frac{\sum_{j\neq i}e^j}{\sum_je^j}\\ &=y_i-1\end{aligned} \]

上面的结果表示，我们只需要正想求出 $y_i$，将结果减1就是反向更新的梯度.

softmax VS k个二元分类器

如果你在开发一个音乐分类的应用，需要对k种类型的音乐进行识别，那么是选择使用 softmax 分类器呢，还是使用 logistic 回归算法建立 k 个独立的二元分类器呢？
这一选择取决于你的类别之间是否互斥，例如，如果你有四个类别的音乐，分别为：古典音乐、乡村音乐、摇滚乐和爵士乐，那么你可以假设每个训练样本只会被打上一个标签（即：一首歌只能属于这四种音乐类型的其中一种），此时你应该使用类别数 k = 4 的softmax回归。（如果在你的数据集中，有的歌曲不属于以上四类的其中任何一类，那么你可以添加一个“其他类”，并将类别数 k 设为5。）
如果你的四个类别如下：人声音乐、舞曲、影视原声、流行歌曲，那么这些类别之间并不是互斥的。例如：一首歌曲可以来源于影视原声，同时也包含人声。这种情况下，使用4个二分类的 logistic 回归分类器更为合适。这样，对于每个新的音乐作品，我们的算法可以分别判断它是否属于各个类别。
现在我们来看一个计算视觉领域的例子，你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是：室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢？ (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片，你又会选择 softmax 回归还是多个 logistic 回归分类器呢？
在第一个例子中，三个类别是互斥的，因此更适于选择softmax回归分类器。而在第二个例子中，建立三个独立的 logistic回归分类器更加合适。

softmax上溢和下溢问题

softmax公式里面因为存在指数函数，所以有可能会出现上溢或下溢的问题。如下面的例子所示：

import math
import numpy as np

def softmax(inp):
    length = len(inp)
    exps = []
    res = 0
    ind = 0
    for item in inp:
        exp = math.exp(item)
        res = res + exp
        exps.append(exp)
        ind+=1
    exps = np.array(exps)   
    return exps/res


inp = [1000,500,500]
inp1 = [-1000,-1000,-1000]
print("上溢:",softmax(inp))
print("下溢:",softmax(inp1))

当指数函数里面传入的值很大时，就会出现上溢，爆出OverflowError.

当指数函数里面传入的值是很小的负数时，就会出现下溢，输出结果就是0，这样就有可能导致分母的值为0。比如，inp=[-1000,-1000,-1000]。

解决这个问题的方法就是利用softmax的冗余性。我们可以看到对于任意一个数a, x-a和x在softmax中的结果都是一样的。

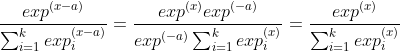
所以，对于一组输入$x=[x_1,x_2,...,x_n]$，我们可以让$a=max(x)$. 这样就可以保证x-a的最大值等于0，也就不会产生上溢的问题。同时，因为一定有 $x-a=0$，, 所以分母的值就不可能为0，也就解决了下溢的问题。大家可以去改改上面的代码看看。

在用梯度下降法最小化交叉熵损失函数的时候，对参数求导需要计算log(softmax)。用这个方法同样可以保证不会出现log(0)的情况，因为softmax的分母至少有一项为1，就不会等于0了。

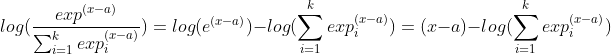
由LogSumExp到Softmax

LogSumExp由来

假设我们有 $N$ 个值的数据集 $\{x_n\}_{n=1}^N$，我们想要求 $z=\log \sum_{n=1}^{N} \exp \left{x_{n}\right} $ 的值，应该如何计算？

看上去这个问题可能比较奇怪，但是实际上我们在神经网络中经常能碰到这个问题。

在神经网络中，假设我们的最后一层是使用softmax去得到一个概率分布，softmax的形式为： $\frac{e{x_{j}}}{\sum_{i=1}^{n} e^{x_{i}}}$

这里的 $x_j$ 是其中的一个值。最终loss函数如果使用cross entropy，那么就涉及到需要对该式求 log ，也就是

\[ \begin{aligned} \log \left(\frac{e{x_{j}}}{\sum_{i=1}{n} e^{x_{i}}}\right) &=\log \left(e^{x_{j}}\right)-\log \left(\sum_{i=1}^{n} e^{x_{i}}\right) \\ &=x_{j}-\log \left(\sum_{i=1}^{n} e^{x_{i}}\right) \end{aligned} \]

这里的减号后面的部分，也就是我们上面所要求的 zz ，即LogSumExp（之后简称LSE）。

特点

因为我们通过softmax想要得到概率分布，假设我们目前有两个例子：一个数据集为 [1000,1000,1000][1000,1000,1000] ，另一个数据集为 [−1000,−1000,−1000][-1000,-1000,-1000] 。

这两组数据在理论上应该得到的概率分布都应该是 $[\frac{1}{3},\frac{1}{3},\frac{1}{3}]$ ，但是实际上如果我们直接按照 $\frac{e{x_{j}}}{\sum_{i=1}{n} e^{x_{i}}}$ 去计算的时候，会发现：

>>> import math
>>> math.e**1000Traceback (most recent call last):
  File "<stdin>", line 1, in <module>OverflowError: (34, 'Result too large')
>>> math.e**-10000.0

可以发现，一个计算不出来，另一个得0，很明显这些结果都是有问题的。实际上在 64-bit 系统中，因为下溢(underflow) 和上溢(overflow) 的存在，我们没有办法精确计算这些值的结果。那么我们就需要别的方法来解决这个问题，这时候我们就需要对该式进行分析。由于在softmax的时候是针对指数进行操作的，值一定会很大，但是之后在计算cross-entropy的时候由于log的存在导致值又回到正常范围。因此我们考虑如何去重写这个正常范围内的值。也就是如何去近似LSE。

近似

我们可以根据指数函数的性质得到

\[ e^a\cdot e^b=e^{a+b} \]

而对于log函数而言，

\[ \log a+\log b = \log (a\cdot b) \]

所以我们可以将LSE重写为：

\[ \begin{aligned} \log \operatorname{SumExp}\left(x_{1} \ldots x_{n}\right) &=\log \left(\sum_{i=1}^{n} e^{x_{i}}\right) \\ &=\log \left(\sum_{i=1}^{n} e^{x_{i}-c} e^{c}\right) \\ &=\log \left(e^{c} \sum_{i=1}^{n} e^{x_{i}-c}\right) \\ &=\log \left(\sum_{i=1}^{n} e^{x_{i}-c}\right)+\log \left(e^{c}\right) \\ &=\log \left(\sum_{i=1}^{n} e^{x_{i}-c}\right)+c \end{aligned} \]

将这个带入到cross-entropy里，那么

\[ \begin{aligned} \log \left(\text {Softmax}\left(x_{j}, x_{1} \ldots x_{n}\right)\right) &=x_{j}-\log \operatorname{Sum} \operatorname{Exp}\left(x_{1} \ldots x_{n}\right) \\ &=x_{j}-\log \left(\sum_{i=1}^{n} e^{x_{i}-c}\right)-c \end{aligned} \]

而对于 [1000,1000,1000][1000,1000,1000] 来说，就变成了

\[ \begin{aligned} \log (\text {Softmax}(1000,[1000,1000,1000])) &=1000-\log (3)-1000 \\ &=-\log (3) \end{aligned} \]

这样就变成了可计算的。

在实际应用中，往往会取到 $c=\max_i x_i$ ，这样保证了取指数时的最大值为0。起码不会因为上溢而报错，即使其余的下溢(underflow)，也可以得到一个合理的值。

性质

LSE函数是凸函数，且在域内严格单调递增，但是其并非处处严格凸（摘自维基百科）

严格凸的LSE应该是 $\left(x_{1}, \ldots, x_{n}\right)=L S E\left(0, x_{1}, \ldots, x_{n}\right)$

首先，如果我们使用线性近似的方法，依据定义 $f(x)\approx f(c)+f’(c)(x-c)$

那么对于$f(x)=\log(x+a)$ 来说，令 $c=x-a$ ，可得

\[ f(x)=\log(x+a)\approx f(x-a)+f’(x-a)\cdot a=\log x+\frac{1}{x}\cdot a \]

因此$\log(x+a)\approx \log x + \frac{a}{x}$

那么 $LSE(x)=\log(\sum_i \exp x_i)\approx \log \left(\exp x_{j}\right)+\left(\sum_{i \neq j} \exp x_{i}\right) / \exp x_{j}$

由于 $\sum_i x_i\leq n\cdot \max_i x_i$ ，且对于正数来说 $\sum_i x_i\geq x_i $，因此

\[ \begin{aligned} \max \left\{x_{1} \ldots, x_{n}\right\} &=\log \left(\exp \left(\max x_{i}\right)\right) \\ & \leq \log \left(\exp \left(x_{1}\right)+\cdots+\exp \left(x_{n}\right)\right) \\ & \leq \log \left(n \cdot \exp \left(\max x_{i}\right)\right) \\ &=\max \left\{x_{1}, \ldots, x_{n}\right\}+\log (n) \end{aligned} \]

即

\[ \max \left\{x_{1}, \ldots, x_{n}\right\}<\operatorname{LSE}\left(x_{1}, \ldots, x_{n}\right) \leq \max \left\{x_{1}, \ldots, x_{n}\right\}+\log (n) \]

因此可以说 $LSE(x_1,…,x_n)\approx \max_i x_i$ ，所以它实际上是针对max函数的一种平滑操作，从字面上理解来说，LSE函数才是真正意义上的softmax函数。而我们在神经网络里所说的softmax函数其实是近似于argmax函数的，也就是我们平时所用的softmax应该叫做softargmax。

Reference

🔖 https://zhuanlan.zhihu.com/p/153535799