本文主要介绍球谐(Spherical Harmonic,简称SH)函数在光照中的一些计算实现,其内容来自于GDC2003的演讲:Spherical Harmonic Lighting: The Gritty Details
学习总结
球谐函数是一组正交基函数,两两相乘的积分结果是0,而自身相乘的积分结果为1,任意信号都可以通过与球谐函数相乘积分算出其在对应球谐函数上的系数,这个过程可以看成是信号在球谐函数上的投影,通过多个球谐函数按照对应系数累加可以得到原始信号的模拟,参与模拟的球谐函数阶数越高,模拟精度也就越高。
球面坐标系(\(\theta, \phi\))下面的球谐函数可以表示任意点到球心的距离,而这个距离也可以解读成强度,从而可以用于实现某点处各个方向上的输入光强。同时,每个点处的输入光强与输出光强的转换关系(BRDF之类)也可以使用球谐函数来表示,实际光照就是上述两个球谐函数相乘的积分输出,而在实际计算中,如果在离线的时候完成两个球谐函数的系数的求取,在运行时只需要一个系数向量点乘即可完成,大大简化了计算量,提升了计算速度。
背景简介
球谐光照(SH Lighting)是Sloan,Kautz以及Snyder大神在2002年的Siggraph上给出的用以实现超真实光照模型渲染的技术。使用SH Lighting可以让我们实现面光源光照模型的计算捕捉存储以及实时重建一个全局光照般的效果。
Siggraph2002的原文实现比较晦涩,对于一些新手来说可能不太友好,而本文则会对SH实现的背景假设以及推导做详细介绍,以达到新手也能快速入门的目的。
光照计算
作为游戏引擎开发者,不能不知道一些光照模型的相关知识。所有光照模型中最简单的一种应该就是diffuse surface reflection model了,因为这个模型中核心的计算就是对光照方向与表面法线方向进行点乘,而得名"dot product lighting"(点乘光照)。
对于场景中存在多个光源,每个光源的光照强度(intensity)都用RGB来表示的话,那么某个像素的最终反射光亮度(Irradiance)就可以表示成如下的公式:
其中\(L_i\)表示的是第\(i\) 个光源的光照方向,\(N\) 表示像素的世界法线,\(lightcol_i\) 则是第\(i\) 个光源的光照强度,surfacecol是当前像素的基色(diffuse/albedo?)。
上述的公式是处于对计算时间的考虑而进行的对真实的物理渲染公式的一个简化处理,真实的物理渲染公式由于过于复杂而无法实现实时计算:

在真实的物理渲染公式中:
- \(L(x, \vec{w_o})\) 指的是从当前像素反射而出的朝着 \(w_o\) 方向反射的光照强度;
- \(L_e(x, \vec{w_o})\) 指的是当前像素自发光的强度;
- \(f_r(x, w_i\rightarrow\vec{w_o})\)指的是当前像素点对应的入射方向为\(w_i\),出射方向为 \(w_o\) 的BRDF(Bilateral Reflectance Distribution Function);
- \(L(x^{'}, \vec{w_i})\)指的是从其他位置\(x^{'}\) 沿着 \(w_i\) 方向反射到当前像素上的光照强度;
- \(G(x, x^{'})\)指的是当前像素 \(x\) 与 光源 \(x^{'}\) 之间的几何关系函数;
- \(V(x, x^{'})\)指的是 \(x\) 与 \(x^{'}\) 之间的可见性函数。
从这个公式可以看出,当前像素 \(x\) 沿着 \(w_o\) 方向出射的光照强度等于两个部分之和:其一是自发光强度,其二是反射光强。其中反射光强是最为复杂的一项:由各个方向的入射光考虑可见性以及几何关系之后积分而成。
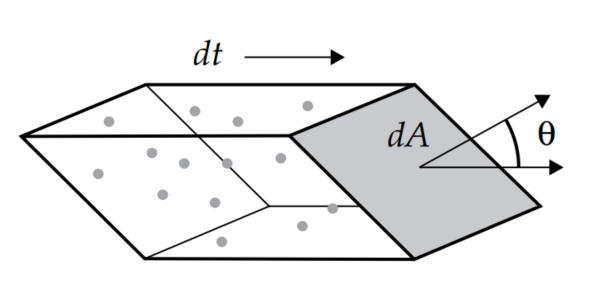
如上图所示,假设不考虑时间的流动,在一个装满光子的空间volume中,可以认为每个位置的光子密度是均匀的常量;而如果假设这个volume中的光子都沿着某个固定的方向匀速流动,那么在一定的时间段内,就会有一定数量的光子穿过流动方向成一定夹角的截面,为了进行定量的分析,我们需要检测单位时间内穿过截面的光子数量,这个检测的结果称为flux,通常用joules/second(J/s,也就是watt)为单位。
而从空间几何关系计算,可以得知,flux的数值与截面法线方向跟流动方向夹角的余弦成正比,夹角越大(比如前面两个方向越接近垂直的话),余弦越小,flux数值越小。
为了表征光子密度流速以及截面之间的关系,我们将flux除以截面的面积,就得到了单位时间流经单位截面面积的光子数目,这个数值通常用光辐射照度irradiance来表示,其单位为\(w/m^2\)。
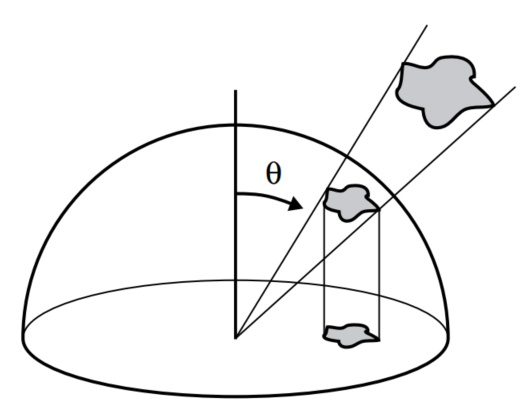
irradiance考虑的是单位面积下的光照强度,不过按照主观意识,可以知道,光强是随着距离而递减的,如果将光源看成是球面输出模型的话,那么就可以理解成,距离越远,球面表面积就越大,此时均分得到的光强自然越弱,但实际上一束光线沿着某个固定的方向射出,不考虑途中的损耗,其光强应该是不随距离的变化而变化的,为了表征这个特性,引入单位固体角下的光辐射照度这个表达项,这个数值通常称为光照亮度radiance,其单位为w/(m2*sr),sr是固体角的单位。
如果对上图中的volume的边长进行缩小逼近,我们可以得到一个微分 (\(dA, dt, d\Omega\)) 的volume模型,,这个模型可以用来近似单束光的数值表现,之后根据需要进行积分运算就能得到实际需要的各种结果。
这里简要介绍了物理真实的光照渲染模型的一些基本背景以及实现公式,之后要考虑的就是怎样将这个实现公式用在实时渲染中,下面将会介绍实际渲染中使用的各种模拟逼近方法。
蒙特卡罗积分
我们现在已经有一个输入光强作为变量的积分函数光照模型,不过由于目前这个模型还存在很多不明确的部分,使得我们无法通过符号运算的方法直接给出积分结果。对于这种情况来说,蒙特卡罗积分方法是一个比较合适的计算方法,蒙特卡罗算法主要的计算过程都是通过概率论的方法完成的,所以不需要了解那些不明确部分的具体数值或规律。
先来介绍一下概率论的一些基础知识。一个随机变量指的是在一个指定的定义域中按照某种分布规律输出对应数值的变量。比如我们要抛一个六面的骰子,那么出现1~6中任意一个数值的概率都是1/6,这个我们抛出的数值x就是一个随机变量。
随机变量x出现的规律我们称之为概率分布函数(probability distribution function, PDF),简称\(P(x)\),\(P(x)\) 是一个输出数值永远都为正数的函数,且对相应的随机变量按照全定义域进行积分或者求和,得到的结果一定为1。
对于出现数值小于某个指定数值 \(x\) 的概率称之为累计概率函数(cumulative distribution function, CDF),简称\(C(x)\)。\(P(x)\) 与 \(C(x)\) 之间的关系是导数与积分的关系:对 \(C(x)\) 进行微分(连续)或者差分(离散)就得到了 \(P(x)\),对 \(P(x)\) 进行积分(连续)或者求和(离散)就得到了 \(C(x)\)。在刚才的骰子实验中,\(P(x) = 1/6, C(x) = x/6\)(此处假设分布式连续的,而非离散变量)。此外对于出现任一数值的概率都相同的分布函数,我们称这个随机变量符合均匀分布(uniform distribution),这个随机变量成为均匀随机变量。其中定义域为[0,1)的连续均匀随机变量由于在采样理论中会经常出现,我们这里给其设定一个专有的名字:归一化均匀随机变量(canonical random variable),且为其设置一个专有符号 ξ(/ksi/)。
随机变量x出现在[a,b]范围内的概率,可以通过积分得到:
每个由随机变量 \(x\) 作为自变量的函数 \(f(x)\) 都能够计算得到一个平均值,这个平均值我们称之为 \(f(x) \)的期望值 \(E[f(x)]\)。
假设某个均匀随机变量的定义域为[0,2](可以计算出P(x) = 1/2),而以x作为自变量的函数\(f(x) = 2 - x\);可以计算得到其期望值:
除了上述直接通过符号化的公式计算函数的期望值之外,我们还可以通过采样足够多的的数据(大数定理)来进行数值的模拟(蒙特卡罗估计方式):
根据这个期望的计算公式,我们可以推导出一个积分公式如何转换为一个求和计算公式,这个公式就称之为蒙特卡罗估计公式:
这个公式表达的意思是,一个积分公式,可以转换为一个采样点除以采样值出现概率之后的平均期望。而从这个公式可以看到,当积分函数f(x)与概率函数p(x)的一致性越高,那么\(f(x)/p(x)\)的方差就越低,期望计算时所需要的采样点数目也就越少(保证计算结果精度的前提下),在极端情况,比如 \(f(x) = p(x)\) 的时候(这里说的应该是基本上等于,否则根本无需采样,直接计算就完了),可能只需要一个采样点就足以计算出f(x)的结果。蒙特卡罗估计方式的另一种写法是将\(1/p(x)\) 用 \(w(x)\)来表示(权重相乘求和):
这个公式的直观意义是,出现概率越大的采样数值,在积分中贡献的权重越低(因为出现概率越大,说明在采样结果列表中出现的频次越高,而积分的意义却是每个值只出现一次,所以从这个角度来看,这种处理是符合实际需要的)。
按照这个公式,假如我们能够保证概率分布函数\(p(x)\) 是一个均匀概率函数的话,此时\(p(x) = 1/N\),前面的求和公式就可以近似为\(\sum f(x_i)\),那么我们在计算图形积分的时候,只需要通过点采样(point sample)后求和,就能够得到积分的近似结果了。
现在回到前面的物理真实的渲染公式,这个渲染公式是一个对半球的积分,这个积分可以通过在半球上均匀散布的采样点(更专业一点的说法叫做无偏随机采样点:unbiased random samples)进行采样求和计算来近似。这里需要两个相互独立的均匀随机变量 \(ξ_x\) 以及 \(ξ_y\),这两个变量分别代表了横竖垂直的两个采样方向,其表征的范围是一个方形区域,通过下面的公式,可以转换成球面坐标:
平面坐标到球面坐标的转换
由于对于整个球面的采样点是均匀分布的,也就意味着各个采样点之间的概率对于整个球面分布而言是相同的常量,而球面的表面积公式为 \(4\pi R^2\) ,其中R = 1,可以简化为4π,球面上任意一点出现的概率就应该是1/4π,对应的公式计算中的权重函数\(w(x) = 4π\). 根据这种分布方式得到的采样点分布大致如下图所示:
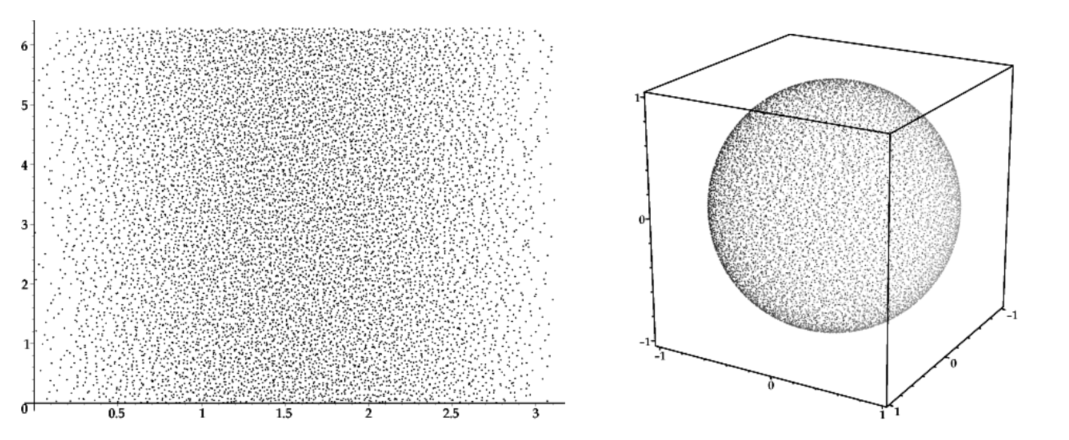
蒙特卡罗积分公式是对期望积分的模拟与简化,而采样点相对于期望值越分散(方差越大),表明对应函数曲线突变越明显,此时模拟的精度就越差,而在实际使用中,通常可以使用一种分层采样(stratified sampling)的方法来降低方差。这种方法是如何实现的呢?那就是将输入的方块区域分割成N x N个cell单元组成的细小网格,之后在每个cell中生成随机采样位置(cell中的采样点称为抖动采样点,jittered sample)进行采样。
这里有个问题,如果cell都是等大的,那么怎样才能保证不同区域的采样点密度不一样呢?实际上,之所以称为分层采样,是因为采样点并不是统一在一起的,而是分为多层进行,比如这里的这个例子,就可以分成两层进行采样:
1. 先将\((θ,φ)\)坐标空间先均匀分成\(M\times M\)个方形区域,每个方形区域中指定其分割的份数\(N_i\):出现概率越高,\(N_i\)越大,从而保证在低概率区域采样点数目少于高采样点区域;
2. 在每个方形区域进行进一步的细分,分割成\(N_i\times N_i\)个cell,每个cell生成一个随机点。
所谓的分层采样,是根据一些先验条件对采样位置进行人为干预以降低方差的方法,为什么这种方式可以降低方差呢,其实就跟曲线拟合是差不多的,在变化陡峭的地方增加一些采样点,在变化平缓的地方减少采样点,从而保证最终的曲线拟合精度足够高。
经过证明,使用分层采样方式得到的采样结果中,每个cell的采样方差之和不会大于未分层之前的采样方差,实际情况中通常要远远低于这个值。当然,在实际应用中还有许多小trick可以增加蒙特卡罗积分的精确性,不过对于基本的SH光照计算来说,分层采样就已经够用了。
下面给出为某个方块生成抖动采样点(每行cell数目为sqrt_n_samples)并计算每个采样点的SH系数的示例代码:
struct SHSample
{
Vector3d sph;
Vector3d vec;
double *coeff;
};
void SH_setup_spherical_samples(SHSample samples[], int sqrt_n_samples)
{
// fill an N*N*2 array with uniformly distributed
// samples across the sphere using jittered stratification
int i=0; // array index
double oneoverN = 1.0/sqrt_n_samples;
for(int a=0; a<sqrt_n_samples; a++)
{
for(int b=0; b<sqrt_n_samples; b++)
{
// generate unbiased distribution of spherical coords
double x = (a + random()) * oneoverN; // do not reuse results
double y = (b + random()) * oneoverN; // each sample must be random
double theta = 2.0 * acos(sqrt(1.0 - x));
double phi = 2.0 * PI * y;
samples[i].sph = Vector3d(theta,phi,1.0);
// convert spherical coords to unit vector
Vector3d vec(sin(theta)*cos(phi), sin(theta)*sin(phi), cos(theta));
samples[i].vec = vec;
// precompute all SH coefficients for this sample
for(int l=0; l<n_bands; ++l)
{
for(int m=-l; m<=l; ++m)
{
int index = l*(l+1)+m;
samples[i].coeff[index] = SH(l,m,theta,phi);
}
}
++i;
}
}
}正交基函数(Orthogonal Basis Functions)
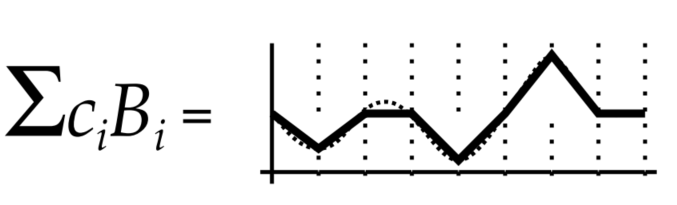
正交基函数是一组相互正交的基础函数(类似于相互垂直的坐标轴,这里的正交指的是任意两个基函数相乘后的结果的积分都是0,而基函数本身相乘后的积分结果为1),通过这些基函数的线性组合,可以实现一些复杂函数(信号)的模拟:
\(B_i(x)\) 为基函数,\(c_i\) 是此基函数的加权系数。在给定基函数的前提下,求取 \(f(x)\) 对应的各个基函数的系数 \(c_i\) 的过程,称为投影。根据基函数的特性,我们可以通过对\(f(x) * B_i(x)\)进行积分来求取\(c_i\)。
候选基函数有许多,而其中一些非常有意思的函数被数学家单拎出来组成了一个基函数组,并被冠名正交多项式(orthogonal polynomial,这个基函数组内的基函数存在以下的积分特性:
而如果我们对上述公式中返回的结果做进一步限制,比如将返回值设定为0,或者1(而非c)的话,那么这个基函数组就缩小为归一化正交基函数(othonormal basis function),这类多项式正交基函数通常会以它们的研究者命名,其中最让人感兴趣的一组函数被称作"勒让德多项式(Legendre Polynomials,此处我们指的是更为细分的伴随勒让德多项式,Associated Legendre Polynomials)"。
勒让德多项式通常用符号 \(P\) 表示,而伴随勒让德多项式一共包含两个参数 \(l\) 与 \(m\),这些多项式的定义域为\([-1, 1]\),其中普通勒让德多项式返回的结果是复数域的,而伴随勒让德多项式返回的结果是实数域的。

伴随勒让德多项式的两个参数 \(l\) 跟\(m\) 会将这个基函数组分割成更为细分的单位,其中处于同一个 \(l\) 中的多个基函数称为这些函数处于一个函数带中(band of functions),而 \(l\) 被称为带系数(band index),其取值范围为任意非负整数,确定了 \(l\) 之后,\(m\) 的取值范围就变成了 \([0, l]\),按照这个命名规则,伴随勒让德多项式矩阵应该是一个三角形状:
处于同一个带内的勒让德多项式其正交的结果(也就是相乘后的积分结果)为某一个常数c1,而不同带内的勒让德多项式的正交结果为另一个常数c2.
勒让德多项式的处理过程通常比较耗时,因此很少用于对一维函数的模拟,且这个系列的基函数通常是面向导数定义的,且处理过程非常繁琐,这个过程对于浮点数计算非常不友好。因此,出于简化处理的考虑,我们此处会利用前后多项式的关系(比如按照递归方式)来根据前面的生成结果生成后续的多项式,这种生成方式只需要遵循三条规则:
这是我们给出的多项式生成规则中最主要的一条,利用前面两个band的多项式直接计算出当前band对应的多项式,不过注意,这个公式中由于存在 \(P^m_{l-2}\) 部分,也就隐式包含了其使用限制:\(l-2 >= m\)。也就是说无法处理\(m = l\) 以及 \(m + 1 = l\) 这两种情况,因此给出了下面的两条补充规则:
这个规则主要用于处理规则1中的m无法等于l的漏洞,且这个公式计算得到的多项式不需要前面band的多项式结果。注意,公式中的两个感叹号指的是对这个值进行双阶乘(注意,负奇数的双阶乘是其绝对值的双阶乘的倒数,负偶数的双阶乘是无意义的),其结果是所有不大于2m -1的奇数相乘,将m = 0代入公式得到 \(P_0^0(x=1)\)。
规则3给出了\(l = m + 1\) 的补充规则。
有了这三条规则,我们就能够生成整个勒让德多项式矩阵了,其使用方式是先根据规则2生成 \(P_m^m\)
(对应于之前的勒让德多项式矩阵的斜边),之后根据规则3生成 \(p_{m+1}^m\)(对应于勒让德多项式矩阵的次斜边,也就是斜边各元素正下方的第一个元素),之后根据规则1,填充剩余的各个元素。注意,使用规则1计算得到的多项式结果其四舍五入误差要小于按照规则3计算得到的结果(怎么看出来的?另外,这两个公式的应用范围没有重叠,也没有办法比较误差吧?),计算代码给出如下:
def P(l, m, x):
# evaluate an Associated Legendre Polynomial P(l,m,x) at x
pmm = 1.0
if m > 0:
somx2 = np.sqrt((1.0 - x) * (1.0 + x))
fact = 1.0
for i in range(1, m + 1):
pmm *= (-fact) * somx2
fact += 2.0
# Rule 2
if l == m:
return pmm
# Rule 3
pmmp1 = x * (2.0 * m + 1.0) * pmm
if l == m + 1:
return pmmp1
# Rule 1
pll = 0.0
for ll in range(m + 2, l + 1):
pll = ((2.0 * ll - 1.0) * x * pmmp1 - (ll + m - 1.0) * pmm) / (ll - m)
pmm = pmmp1
pmmp1 = pll
return pll
# 测试例子
l = 3
m = 2
x = 0.5
print(P(l, m, x))球谐函数(Spherical Harmonics)
前面介绍的都是一些基础的数学知识,那么这些知识跟球谐函数有什么关系呢?从前面的公式中可以看出,勒让德多项式表达的是对一维信号的模拟实现,而对于二维三维以及更高维的信号,比如二维球面上的数据信号,又该如何表达呢?
实际上,球面二维信号有一种经典的表达方式,这种方式叫做Spherical Harmonic,简称SH(球谐函数),这种数学系统其实跟傅里叶变换比较类似,不过是直接定义在球面上的,其核心的算法就跟勒让德多项式有关。
球谐函数原本是定义在虚数空间,不过我们此处只关心实数域的模拟(比如球面上的光照强度),因此本文后续介绍的所有内容都是跟实数域SH相关的,如果不做解释,默认指的实数域的SH。
单位半径球面上的点的笛卡尔坐标与标准参数化方式得到的球面坐标存在着以下关系:
经典的球谐函数公式形式给出如下,可以看到其核心的部分是以\(\cos(\Theta)\) 为自变量的勒让德多项式,前面提到的一维多项式怎么表达二维信号的问题,从这个公式中可以得到解决,即将一维勒让德多项式作为核心组成部分,分别揉入二维信号的自变量 (两个角度\(θ,φ\)), 就得到了两维信号的表达:
其中\(P_l^m\) 项是伴随勒让德多项式,\(K_l^m\) 是用于进行归一化处理的scale因子:
为了能够表达所有的球谐函数,此处的I跟m的定义跟前面伴随勒让德函数中的定义有所区别:
m不再是\([0,l]\),而是\([-l,l]\)。
\(y_l^m\) 就是对应于伴随勒让德多项式 \(P_l^m\) 的一个分量,将 \(y_0^0\)~\(y_n^n\) 的多个分量加起来,得到的就是球面信号的一个近似模拟,而由于各个分量是相互独立的,因此可以将球谐信号看成是各个球谐分量按照顺序逐一发生的信号,从而可以展开成多个一维的信号(其实就是将之前的三角形排布的信号按照顺序放到同一行中):
第\(i\)个分量就是前面勒让德多项式矩阵中第\(i\)个元素,其实现代码给出如下:
# 计算阶乘
def factorial(n):
if n == 0 or n == 1:
return 1
else:
return n * factorial(n - 1)
# 计算球谐函数的归一化常数
def K(l, m):
temp = ((2.0 * l + 1.0) * factorial(l - m)) / (4.0 * np.pi * factorial(l + m))
return np.sqrt(temp)
# 计算关联勒让德多项式
def P(l, m, x):
pmm = 1.0
if m > 0:
somx2 = np.sqrt((1.0 - x) * (1.0 + x))
fact = 1.0
for i in range(1, m + 1):
pmm *= (-fact) * somx2
fact += 2.0
if l == m:
return pmm
pmmp1 = x * (2.0 * m + 1.0) * pmm
if l == m + 1:
return pmmp1
pll = 0.0
for ll in range(m + 2, l + 1):
pll = ((2.0 * ll - 1.0) * x * pmmp1 - (ll + m - 1.0) * pmm) / (ll - m)
pmm = pmmp1
pmmp1 = pll
return pll
# 计算球谐函数
def SH(l, m, theta, phi):
sqrt2 = np.sqrt(2.0)
if m == 0:
return K(l, 0) * P(l, m, np.cos(theta))
elif m > 0:
return sqrt2 * K(l, m) * np.cos(m * phi) * P(l, m, np.cos(theta))
else:
return sqrt2 * K(l, -m) * np.sin(-m * phi) * P(l, -m, np.cos(theta))
# 测试例子
l = 3
m = 2
theta = np.pi / 4
phi = np.pi / 2
print(SH(l, m, theta, phi))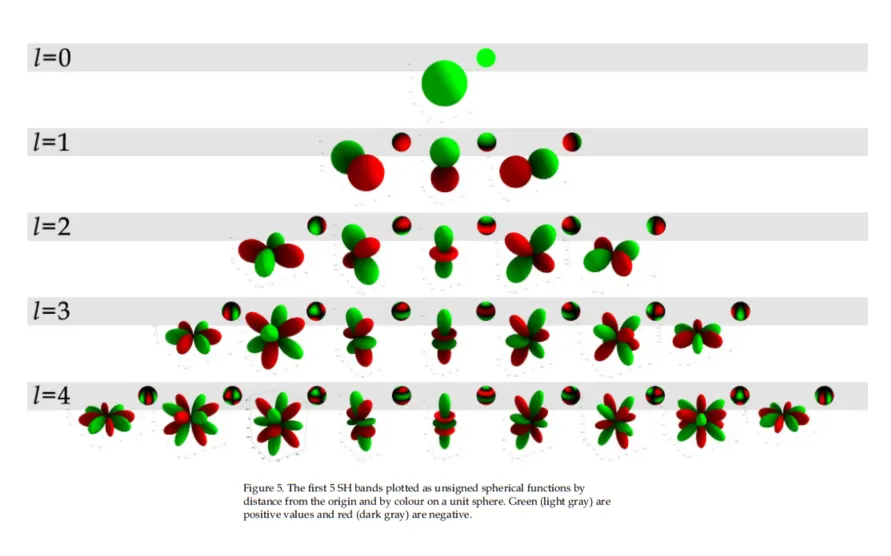
上图给出了前面5个band的球谐函数的图形展示,其中球谐函数的数值用的是到圆心的距离来表示(比如 \(P_0^0(x)=1\),因此\(l=0\) 的时候,就是一个等距球面),而由于m的取值范围是[-l, l],因此,红色绿色分别表示cos(theta)是正负两种情况下的结果。
最终在使用的时候,将这些不同参数下的球谐函数作为基函数,通过线性组合的方式就能够进行二维信号的模拟表达(就像前面一维基函数通过线性组合就能够对给出的一维信号进行模拟一样,以\(\theta, \phi\)作为自变量,到球心的距离作为因变量,看起来像是三维信号)
球谐投影(SH Projection)
在已知球谐函数的前提下,计算某个函数对应于这个函数的系数的过程比较简单:只要将两个函数相乘之后积分即可:
在上面这个公式里,积分的自变量s指的是所有采样点,后续会对这个公式进一步具象成球面参数坐标变量作为自变量的形式。
在得到球谐基函数的系数之后,通过系数相乘求和的方式,就能得到原函数的一个近似模拟:
从这个公式可以知道,为什么说n阶的模拟实现需要\(n^2\) 个球谐系数了。另外,当n越大,这个近似函数就越接近于原函数。不过通常使用的是有限 \(n\) 的版本,这种模拟近似也被称作带限模拟(band-limited approximation)。
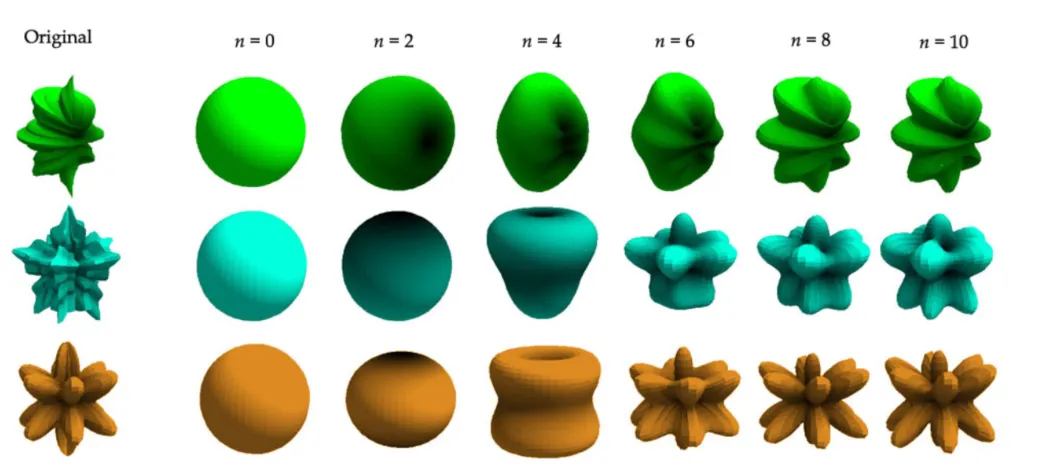
下面通过一个示例介绍如何通过蒙特卡罗积分实现球谐投影以计算得到各个球谐基函数的系数。
第一步需要对球面进行参数化,这里使用的是之前球谐函数使用的的球面坐标系统的参数化方式。
第二步则是选择一个低频函数来进行投影(低频则保证了较少的系数就可以得到较为精确的模拟,band越低,频率越低),这里选定了两个相互垂直的大型单色光源作为待模拟函数,下面的公式给出了这个函数的球面坐标表示方式,不过在实际的实现程序中,我们会直接使用光线追踪的方式从几何的角度直接评估此类函数:
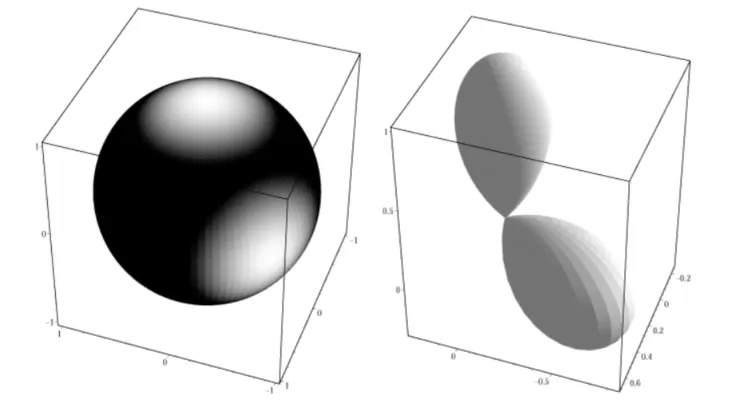
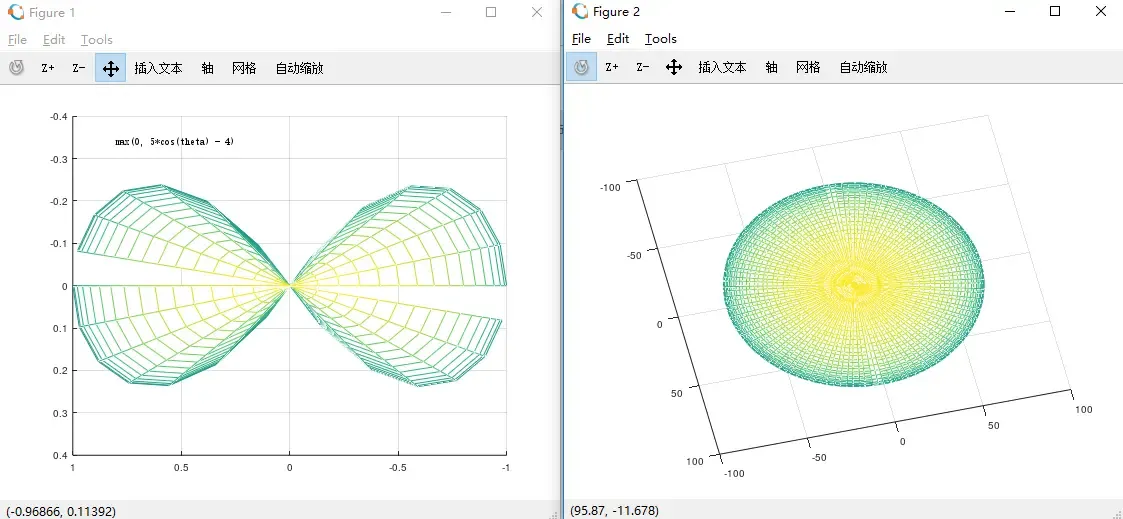
球面积分公式给出如下:
大家可能会好奇,这个积分公式中为什么会有一个sin(theta)项。这是因为,所谓的积分其实就是将小块面积进行累加,当小块的面积足够小的时候,就逼近于积分了。而组成球面的一个个小块(按照角度划分)在赤道附近的面积要大于两极位置的面积,而这个sin就是为了来表示这个含义而增加的。
将这个公式跟前面的球谐函数系数求取公式结合起来,可以得到如下的参数化球谐系数投影函数(SH Projection):
这个公式其实已经算是比较明晰了,通过一些常用的数学软件(比如mathematics或者maple)是可以从符号数学的角度推导出结果的,不过我们在实际应用中是没有这些软件的,只能通过蒙特卡罗积分这种数值分析类的方式来求得结果:
这个公式中的 \(x_j\) 指的是采样点,而\(f(x_j) = light(x_j)y_i(x_j)\),由于我们前面说到,我们的样本都是无偏样本,因此每个样本的概率应该都是相同的,也就是说 \(w(x_j)\) 应该是一个常量(\(1/(1/4π) = 4π\))。而无偏采样的另一个特性就是不论按照什么样的参数化方式,都应该以相同的概率得到相同的采样样本,因此,前面的双重积分可以直接用蒙特卡罗的简化版积分来模拟:
通过蒙特卡罗积分公式,可以我们需要的球谐基函数进行预计算,其实现代码非常简单:
typedef double (*SH_polar_fn)(double theta, double phi);
void SH_project_polar_function(SH_polar_fn fn, const SHSample samples[],
double result[])
{
const double weight = 4.0*PI;
// for each sample
for(int i=0; i<n_samples; ++i)
{
double theta = samples[i].sph.x;
double phi = samples[i].sph.y;
for(int n=0; n<n_coeff; ++n)
{
result[n] += fn(theta,phi) * samples[i].coeff[n];
}
}
// divide the result by weight and number of samples
double factor = weight / n_samples;
for(i=0; i<n_coeff; ++i)
{
result[i] = result[i] * factor;
}
}通过这段代码,我们可以计算我们之前光源进行投影可以得到以下系数:

根据这些系数进行重构得到了如下结果:
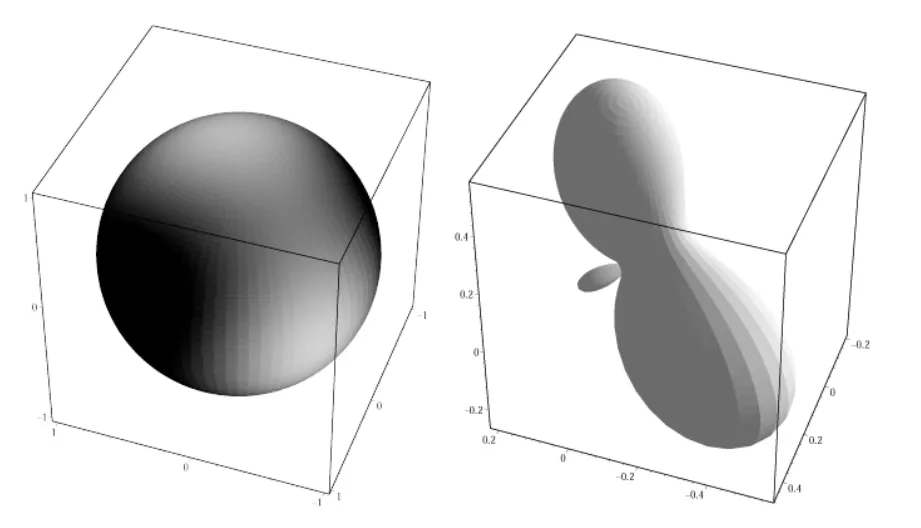
由于只使用了16个系数的SH模拟,所以这个模拟表现应该算得上非常不错了。不过右边这张图上出现了一个增生,这种增生在渲染中的表现就是背部无光区域会出现一块异常的亮斑,之所以会出现这种异常,是因为我们将SH中高频的部分通过max(clamp)去掉了,导致信号的不连续,当我们使用越来越高阶的SH来进行模拟的时候,这个部分的增生会逐渐消退,而为了能够使用低阶SH模拟的时候也能得到较好效果,就需要在光源的设计上下功夫,比如在进行模拟之前,先将光源通过一个窗口函数(比如高斯函数,低通滤波)干掉高频数据,从而避免上述瑕疵。
SH函数属性
相对于其他可选的基函数,SH函数有很多非常适合用来进行光照计算的属性:
- 比如SH函数是归一正交的,也就是任意两个球谐函数相乘之后的积分只有当这两个函数完全相同时,结果为1,其他情况为0.
- SH函数是旋转不变的,也就是说将某个函数 \(f\)旋转后得到 \(g\)函数,这两个函数之间存在如下的关系(球谐模拟后的旋转结果等于旋转后进行球谐模拟的结果,这个特性可以保证在光照位置方向等输入发生了平滑旋转变化的时候,输出也是平滑旋转的,不会出现剧烈突变等瑕疵)
- 两个球谐模拟函数相乘的积分等于对应系数相乘之后求和:
对于光照计算而言,通常需要将输入光 \(L\)与物体表面材质的传递函数 \(t\)(Transfer Function)相乘之后进行球面积分来求取反射输出的光照结果,如果硬算的话基本上是无法做到实时完成的,而使用了球谐函数之后,只需要将L跟t都用球谐模拟的系数表示,根据球谐函数的归一化正交特性,两者相乘之后的积分,就等于对应系数相乘之后求和。
这里给出了球谐函数的一种用法:将两个球谐函数相乘之后的积分,就等于系数相乘之和,其结果是一个标量。除了这种用法之外,球谐函数还可以用来对球谐函数进行转换(transforming)。
比如说,我们有一个光源的球谐函数表示\(a(s)\),以及一个对表面上的点产生遮挡阴影的球谐函数(用于表征当前点周边的遮挡情况的)表示\(b(s)\),如果直接将 \(a(s)\)用作输入光源的SH函数显然是不合适的,因为中间隔着一个\(b(s)\),那么是否可以先将 \(b(s)\)的作用计算出来,在最终进行光照计算的时候利用这个作用先对 \(a(s)\)进行转换,得到遮挡处理后的球谐函数表示 \(c(s)\)呢?其实是可以做到的,通过光线追踪的方式,我们能够将 \(b(s)\)的作用表示成一个传递矩阵(transfer matrix):
这里有两个疑问尚未解决:
1. 这个公式是怎么推导出来的?
2.因为这里相当于三个基函数相乘之后的积分,其结果不能简单通过系数相乘得到,那么这个公式要怎么计算出结果?难道是代入伴随勒让德多项式硬算?
之后将这个矩阵与a(s)的系数进行线性运算,就能得到\(c(s)\)的系数:
这里的积分是对j进行的,是不是意味着可将ai提取出来,放到求和之外,所以整个公式就变成了:\[c_i=\sum_{j=1}^{n^2}\mathbf{M}_{ij}a_i\]
这里用一个实际的例子来阐明这种做法的效果:简单考虑,假如我们的阴影函数就是某个SH基函数\(y_2^2\),那么矩阵元素求取公式就变成了:
这里计算得到的结果是非常稀疏的(0多1少),按照25*25来进行计算,得到的矩阵结果用1表示黑点,0则什么也不绘制,那么其结果图如下所示(难道真的是硬算的?感觉不能做到实时完成?不过因为整个计算过程不需要输入光源的数据,倒是可以通过离线完成):
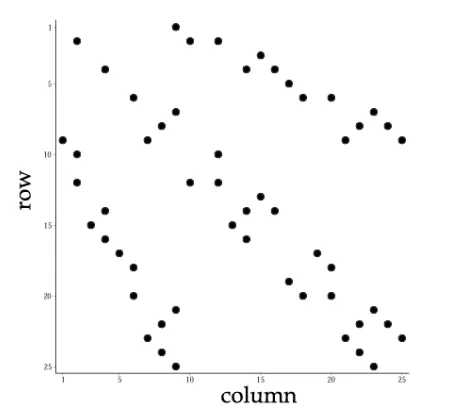
将这个矩阵应用在光源的SH函数上,得到的新的SH函数的系数,其结果就跟将光源的球谐表示与阴影的球谐表示相乘之后的结果差不多,如下图所示:
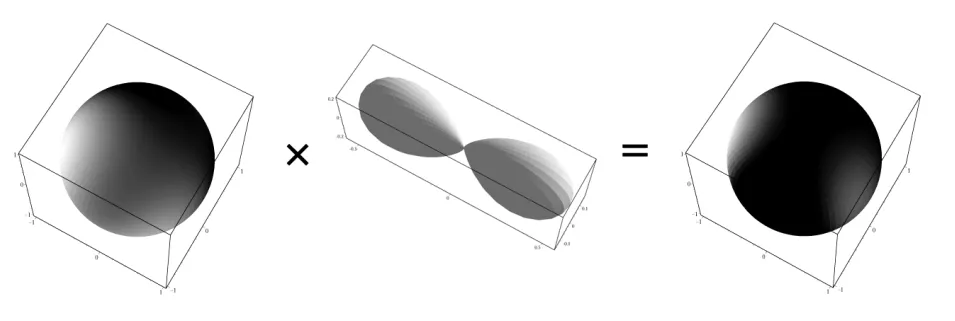
有了这种方法之后,我们可以在不进行最终的光照与投影物之间的交互计算的前提下完成阴影数据的记录。
旋转球谐函数(Rotating SH)
球谐函数的旋转不变特性是最难以理解的,首先需要搞明白的球谐投影函数的旋转是什么意思:按照欧拉角进行旋转?以什么轴序进行?通过\(3\times 3\)旋转矩阵完成?还是通过quaternion完成?
从正交的角度,我们能够理解的旋转过程应该是一个线性操作,且不同band之间的系数是无交互的。按照这种说法,从实际计算的角度出发,我们可以表示为:我们可以通过\(n^2 \times n^2\)的块状对角矩阵(如下图所示的格式,块状是因为band之间的系数是存在交互的)将某个SH向量(系数组成的向量)转换成另一个SH向量:
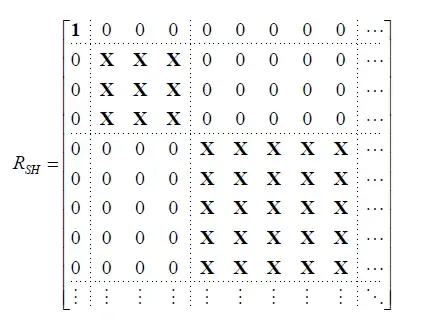
在旋转矩阵中元素已知的情况下实现旋转是一个简单地过程,不过矩阵元素的计算却不简单。为了解释这个过程,我们来看下球谐基函数表示的另一种形式——前面用的是球面坐标形式,现在转换到笛卡尔坐标形式:
这种格式的SH当然也可以如球面坐标形式一样用来进行投影以求取对应的系数,不过更常用的做法是用来进行符号运算。通过对旋转过的SH样本与未旋转过的样本相乘之后进行球面符号积分,我们可以构建出前面提到的旋转矩阵:
通过这个\(n^2 \times n^2\)矩阵,我们可以将未旋转的样本转换为旋转后的样本。如果取\(n = 3\),我们将得到由前三个band组成的SH系统的绕着\(z\)轴旋转的\(9\times 9\)旋转矩阵:
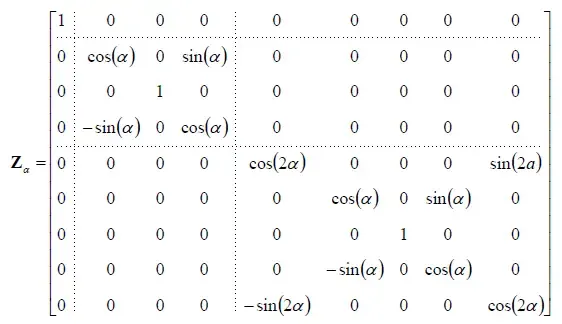
按照上面矩阵的规律,我们可以猜测将这个矩阵扩充到\(N\) band的话,得到的最边缘的非零元素中的角度应该是\(N\alpha\)(准确来说,应该是\((N-1)\alpha\))。
如果只使用低阶的SH函数的话,这种技术就显得非常有用了,我们可以将旋转拆分成多个简单的旋转步骤,之后在得到计算结果后再重新组合出来,在实际使用中,如果SH函数高过两阶,这种技术使用起来就很成问题(什么问题,消耗过高?)。
在使用这个技术之前,我们需要考虑使用哪种旋转拆分方式,可以用最少的步骤达到想要的目的。比如说,如果我们采用ZYZ的旋转方式(欧拉角的旋转方式一共有十二种,采用三个轴组合旋转的有\(A(3,3) = 6\)种,采用两个轴组合旋转的有\(C(3,2) * 2 = 6\)种,注意,两轴旋转需要满足相同两轴并不连续,比如不能出现XXY,只能是XYX),最终可能只需要进行两次旋转就能够达到目标(其中一次已经是我们想要的格式的旋转矩阵?每太看懂这段话,后面再回过头来分析一下),那么要怎么完成对Y轴的旋转呢?这个旋转可以拆分成对X轴的90度旋转后面接一个普通的z轴旋转,之后再接一个x轴的-90度的旋转:
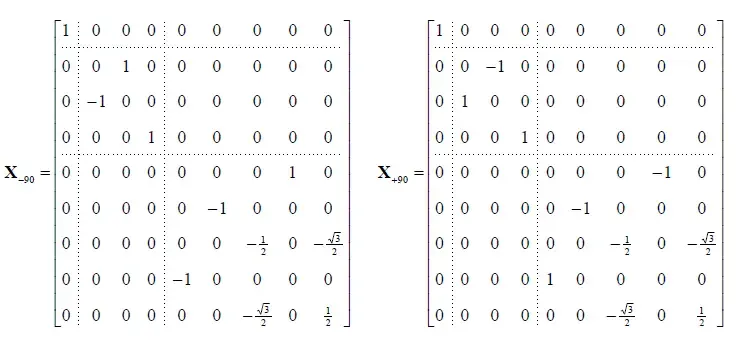
ZYZ形式的旋转,按照上述拆分可以变成如下格式:
整个计算过程需要涉及到4次9x9矩阵的乘法(还没算三角函数的计算消耗),如果矩阵运算的时间复杂度为\(O(n^3)\),那么整个运算过程需要消耗2916个MAD指令,虽然我们可以利用矩阵的稀疏性将5阶旋转矩阵(这里应该说的不是5x5,也不是5次相乘,而是band5(也就是25个系数))的计算消耗降低到340个指令,但是这个消耗依然不低。
那么是否可以将上述的复杂的旋转与乘法操作整合到一个矩阵中呢?实际的结果矩阵比较吓人,比如上述计算结果的二阶表示:
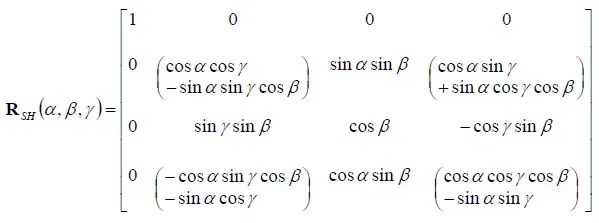
后续还是参考原文吧,看不太懂。。。