概述
Medusa 是自投机领域较早的一篇工作,对后续工作启发很大,其主要思想是 multi-decoding head + tree attention + typical acceptance(threshold)。Medusa 没有使用独立的草稿模型,而是在原始模型的基础上增加多个解码头(MEDUSA heads),并行预测多个后续 token。
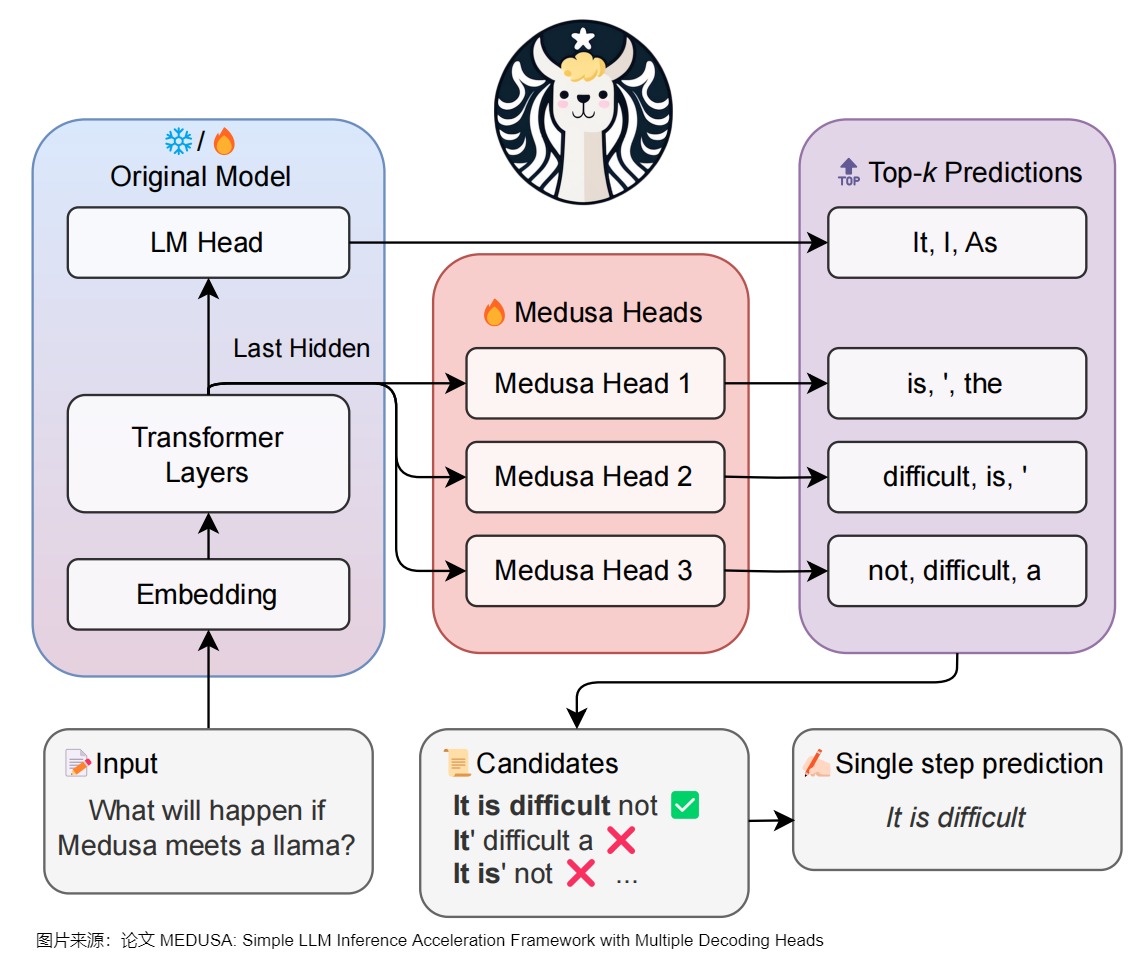
正常的LLM只有一个用于预测 \(t\) 时刻token的head。Medusa 在 LLM 的最后一个 Transformer层之后保留原始的 LM Head,然后额外增加多个(假设是 \(k\) 个) 可训练的Medusa Head(解码头),分别负责预测 \(t+1,t+2,...,\) 和 \(t+k\) 时刻的不同位置的多个 Token。Medusa 让每个头生成多个候选 token,而非像投机解码那样只生成一个候选。然后将所有的候选结果组装成多个候选序列,多个候选序列又构成一棵树。再通过树注意力机制并行验证这些候选序列。
原理

投机采样的核心思路如上图下方所示,首先以低成本的方式(一般来说是用小模型)快速生成多个候选 Token,然后通过一次并行验证阶段快速验证多个 Token,进而减少大模型的 Decoding Step,实现加速的目的。然而,采用一个独立的“推测”模型也有缺点,具体如下:
- 很难找到一个小而强的模型来生成对于原始的模型来说比较简单的token。
- 在一个系统中维护2个不同的模型,即增加了推理过程的计算复杂度,也导致架构上的复杂性,在分布式系统上的部署难度增大。
-
使用投机采样的时候,会带来额外的解码开销,尤其是当使用一个比较高的采样温度值时。
Medua主要借鉴了两个工作:BPD和SpecInfer。 -
大模型自身带有一个LM head,用于把隐藏层输出映射到词表的概率分布,以实现单个token的解码。为了生成多个token,论文“Blockwise Parallel Decoding for Deep Autoregressive Models”在骨干模型上使用多个解码头来加速推理,通过训练辅助模型,使得模型能够预测未来位置的输出,然后利用这些预测结果来跳过部分贪心解码步骤,从而加速解码过程。
- 论文“SpecInfer: Accelerating Generative Large Language Model Serving with Speculative Inference and Token Tree Verification”的思路是:既然小模型可以猜测大模型的输出并且效率非常高,那么一样可以使用多个小模型来猜测多个 Token 序列,这样提供的候选更多,猜对的机会也更大;为了提升这多个 Token 序列的验证效率,作者提出 Token Tree Attention 的机制,首先将多个小模型生成的多个 Token 序列组合成 Token 树,然后将其展开输入模型,即可实现一次 decoding step 完成整个 Token 树的验证。
思路
基于这两个思路来源,Medusa决定让target LLM自己进行预测,即在target LLM最后一层decoder layer之上引入了多个额外的预测头,使得模型可以在每个解码步并行生成多个token,作为“推测”结果。我们进行具体分析。
单模型 & 多头
为了抛弃独立的 Draft Model,只保留一个模型,同时保留 Draft-then-Verify 范式,Medusa 在主干模型的最终隐藏层之后添加了若干个 Medusa Heads,每个解码头是一个带残差连接的单层前馈网络。这些Medusa Heads是对BPD中多 Head 的升级,即由原来的一个 Head 生成一个 Token 变成一个 head 生成多个候选 Token。因为这些 Heads 具有预测对应位置 token 的能力,并且可以并行地执行,因此可以实现在一次前向中得到多个 draft tokens。具体如下图所示。
可能有读者会有疑问,后面几个head要跨词预测,其准确率应该很难保证吧?确实是这样的,但是,如果我每个预测时间步都取top3出来,那么最终预测成功的概率就高不少了。而且,Medusa 作者观察到,虽然在预测 next next Token 的时候 top1 的准确率可能只有 60%,但是如果选择 top5,则准确率有可能超过 80%。而且,因为 MEDUSA 解码头与原始模型共享隐藏层状态,所以分布差异较小。
Tree 验证
因为贪心解码的正确率不够高,加速效果不够显著,因此Medusa让每个Head解码top-k个候选,不同head的候选集合组成一个树状结构。为了更高效地验证这些 draft tokens,Medusa根据这些 Head 生成 Token 的笛卡尔积来构建出多个 Token 序列。然后使用Tree Attention方法,在注意力计算中,只允许同一延续中的 token 互相看到(attention mask),再加上位置编码的配合,就可以在不增加 batch size 的情况下并行处理多个候选。
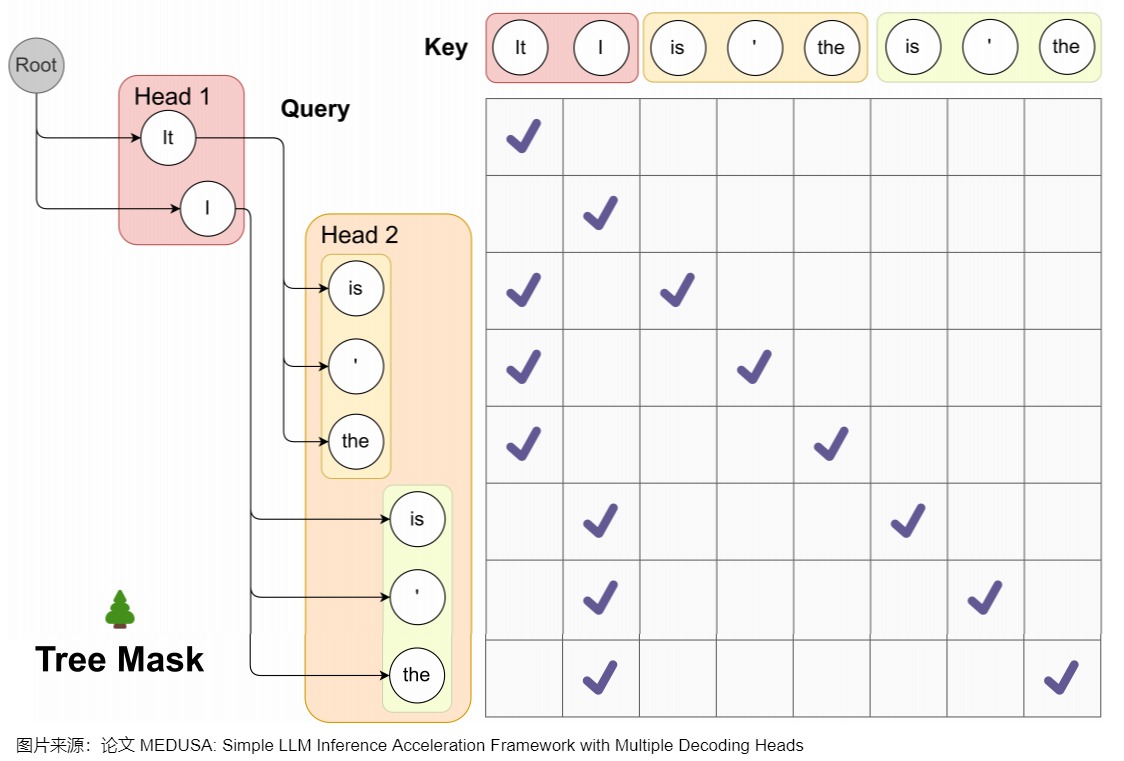
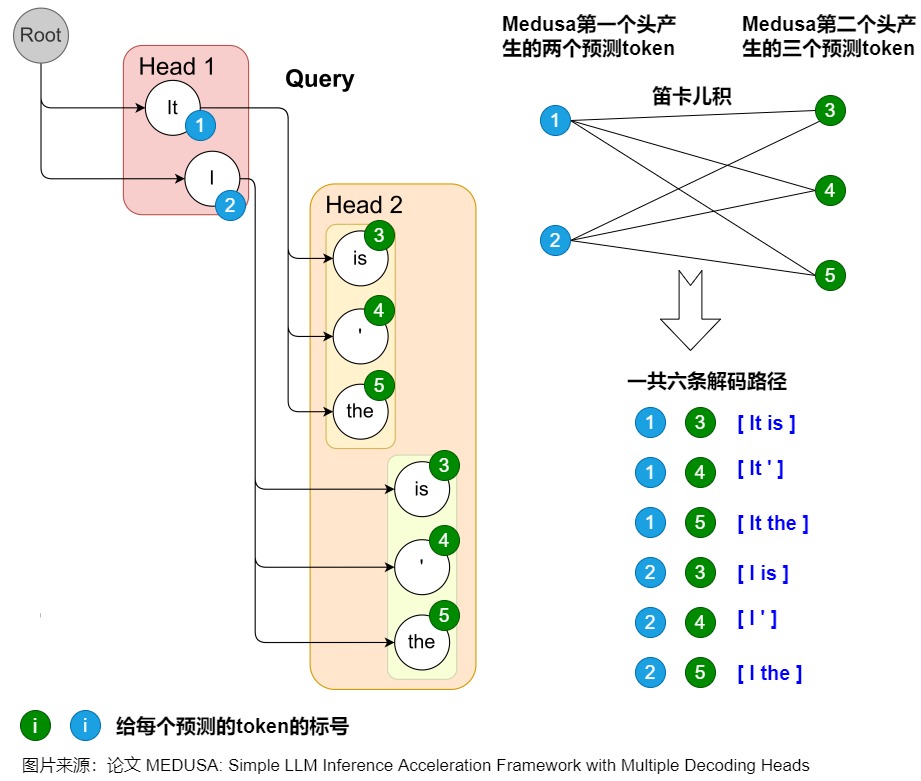
Medusa 中的树和注意力掩码矩阵如下图所示。在每一跳中,我们看到图中Medusa保留了多个可能的token,也就是概率最高的几个token。这样构成了所谓的树结构,直观来说,就是每1跳的每1个token都可能和下1跳的所有token组合成句子,也可以就在这1跳终止。例如,在图中,一共2个head生成了2跳的token,那么这棵树包含了6种可能的句子:Head 1 在下一个位置生成 2 个可能的 Token(It 和 I),Head 2 在下下一个位置生成 3 个可能的 Token(is,’ 和 the),这样下一个位置和下下一个位置就有了 2 x 3 = 6 种可能的候选序列,如下图左侧所示。
而其对应的 Attention Mask 矩阵如右侧所示。与原始投机解码略有不同的地方是,树中有多条解码路径,不同解码路径之间不能相互访问。比如,(1) "It is"和 (2) "I is"是两条路径,那么在计算(1).is的概率分布时,只能看到(1).it,而不能看到(2)中的"I"。因此,Medusa新建了在并行计算多条路径概率分布时需要的attention mask,称为"Tree attention"。本质上就是同一条路径内遵从因果mask的规则,不同路径之间不能相互访问。
Medusa作者称,SpecInfer中每个speculator生成称的序列长度不同,所以Mask是动态变化的。而Medusa的Tree Attention Mask在Infrence过程中是静态不变的,这使得对树注意力Mask的预处理进一步提高了效率。
小结
下表给出了BPD,SpecInfer,Medusa之间的差异。
设计核心
流程
MEDUSA的大致思路和投机解码类似,其中每个解码步骤主要由三个子步骤组成:
- 生成候选者。MEDUSA通过接在原模型的多个Medusa解码头来获取多个位置的候选token
- 处理候选者。MEDUSA把各个位置的候选token进行处理,选出一些候选序列。然后通过tree attention来进行验证。由于 MEDUSA 头位于原始模型之上,因此,此处计算的 logits可以用于下一个解码步骤。
- 接受候选者。通过typical acceptance(典型接受)来选择最终输出的结果。
Medusa更大的优势在于,除了第一次Prefill外,后续可以达到边verify边生成的效果,即 Medusa 的推理流程可以理解:Prefill + Verify + Verify + ...。
模型结构
下面代码给出了美杜莎的模型结构。Medusa 是在 LLM 的最后一个 Transformer Layer 之后保留原始的 LM Head,然后额外加多个 Medusa Head,也就是多个不同分支输出。这样可以预测出多个候选的 Token 序列。
Medusa head的输入是大模型的隐藏层输出。这是和使用外挂小模型投机解码的另一个重要不同。外挂小模型的输入是查表得到的token embedding,比这里的大模型最后一层隐藏层要弱的多,因此比较依赖小模型的性能。正是因为借助大模型的隐藏层输出,这里的Medusa head的结构都十分简单。
class MedusaLlamaModel(KVLlamaForCausalLM):
"""The Medusa Language Model Head.
This module creates a series of prediction heads (based on the 'medusa' parameter)
on top of a given base model. Each head is composed of a sequence of residual blocks
followed by a linear layer.
"""
def __init__(
self,
config,
):
# Load the base model
super().__init__(config)
# For compatibility with the old APIs
medusa_num_heads = config.medusa_num_heads
medusa_num_layers = config.medusa_num_layers
base_model_name_or_path = config._name_or_path
self.hidden_size = config.hidden_size
self.vocab_size = config.vocab_size
self.medusa = medusa_num_heads
self.medusa_num_layers = medusa_num_layers
self.base_model_name_or_path = base_model_name_or_path
self.tokenizer = AutoTokenizer.from_pretrained(self.base_model_name_or_path)
# Create a list of Medusa heads
self.medusa_head = nn.ModuleList(
[
nn.Sequential(
*([ResBlock(self.hidden_size)] * medusa_num_layers),
nn.Linear(self.hidden_size, self.vocab_size, bias=False),
)
for _ in range(medusa_num_heads)
]
)
def forward(
self,
input_ids=None,
attention_mask=None,
past_key_values=None,
output_orig=False,
position_ids=None,
medusa_forward=False,
**kwargs,
):
"""Forward pass of the MedusaModel.
Args:
input_ids (torch.Tensor, optional): Input token IDs.
attention_mask (torch.Tensor, optional): Attention mask.
labels (torch.Tensor, optional): Ground truth labels for loss computation.
past_key_values (tuple, optional): Tuple containing past key and value states for attention.
output_orig (bool, optional): Whether to also output predictions from the original LM head.
position_ids (torch.Tensor, optional): Position IDs.
Returns:
torch.Tensor: A tensor containing predictions from all Medusa heads.
(Optional) Original predictions from the base model's LM head.
"""
if not medusa_forward:
return super().forward(
input_ids=input_ids,
attention_mask=attention_mask,
past_key_values=past_key_values,
position_ids=position_ids,
**kwargs,
)
with torch.inference_mode():
# Pass input through the base model
outputs = self.base_model.model(
input_ids=input_ids,
attention_mask=attention_mask,
past_key_values=past_key_values,
position_ids=position_ids,
**kwargs,
)
if output_orig:
# 原始模型输出
orig = self.base_model.lm_head(outputs[0])
# Clone the output hidden states
hidden_states = outputs[0].clone()
medusa_logits = []
# TODO: Consider parallelizing this loop for efficiency?
for i in range(self.medusa):
# 美杜莎头输出
medusa_logits.append(self.medusa_head[i](hidden_states))
if output_orig:
return torch.stack(medusa_logits, dim=0), outputs, orig
return torch.stack(medusa_logits, dim=0)
Medusa-head
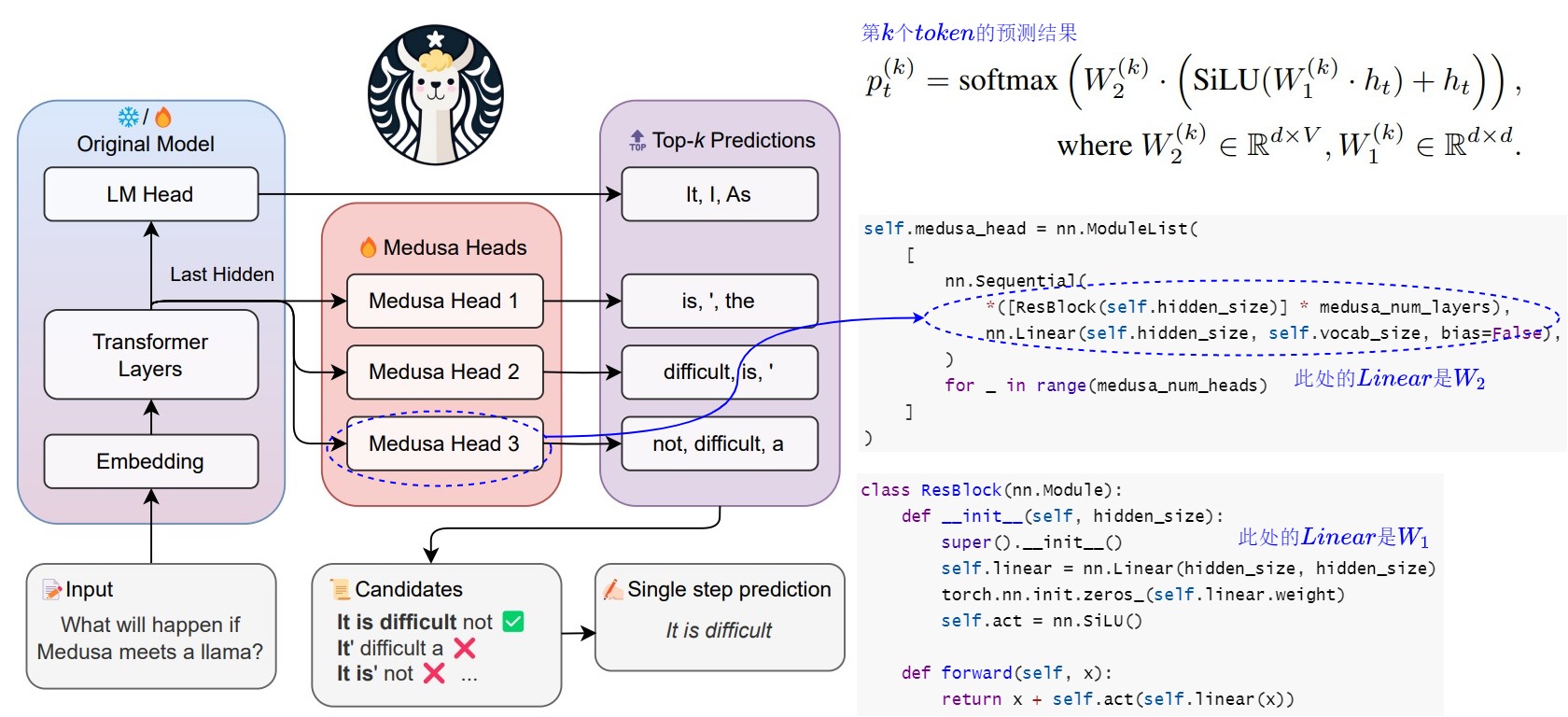
Medusa 额外新增 medusa_num_heads 个 Medusa Head,每个 Medusa Head 是一个加上了残差连接的单层前馈网络,其中的 Linear 和模型的默认 lm_head 维度一样,这样可以预测后续的 Token。
self.medusa_head = nn.ModuleList(
[
nn.Sequential(
*([ResBlock(self.hidden_size)] * medusa_num_layers),
nn.Linear(self.hidden_size, self.vocab_size, bias=False),
)
for _ in range(medusa_num_heads)
]
)
下面代码为打印出来的实际内容。
ModuleList(
(0-3): 4 x Sequential(
(0): ResBlock(
(linear): Linear(in_features=4096, out_features=4096, bias=True)
(act): SiLU()
)
(1): Linear(in_features=4096, out_features=32000, bias=False)
)
)
把第 \(k\) 个解码头在词表上的输出分布记作 \(p^{(k)}_t\),其计算方式如下。\(d\) 是hidden state的输出维度,\(V\)是词表大小,原始模型的预测表示为 \(p^{(0)}_t\) 。
$$
p_t^{(k)} = \text{softmax}\left(W_2^{(k)} \cdot \left(\text{SiLU}\left(W_1^{(k)} \cdot h_t\right) + h_t\right)\right)\
Where\ W_2^{(k)} \in \mathbb{R}^{d \times V}, \quad W_1^{(k)} \in \mathbb{R}^{d \times d}
$$
下面是把代码和模型结构结合起来的示意图。
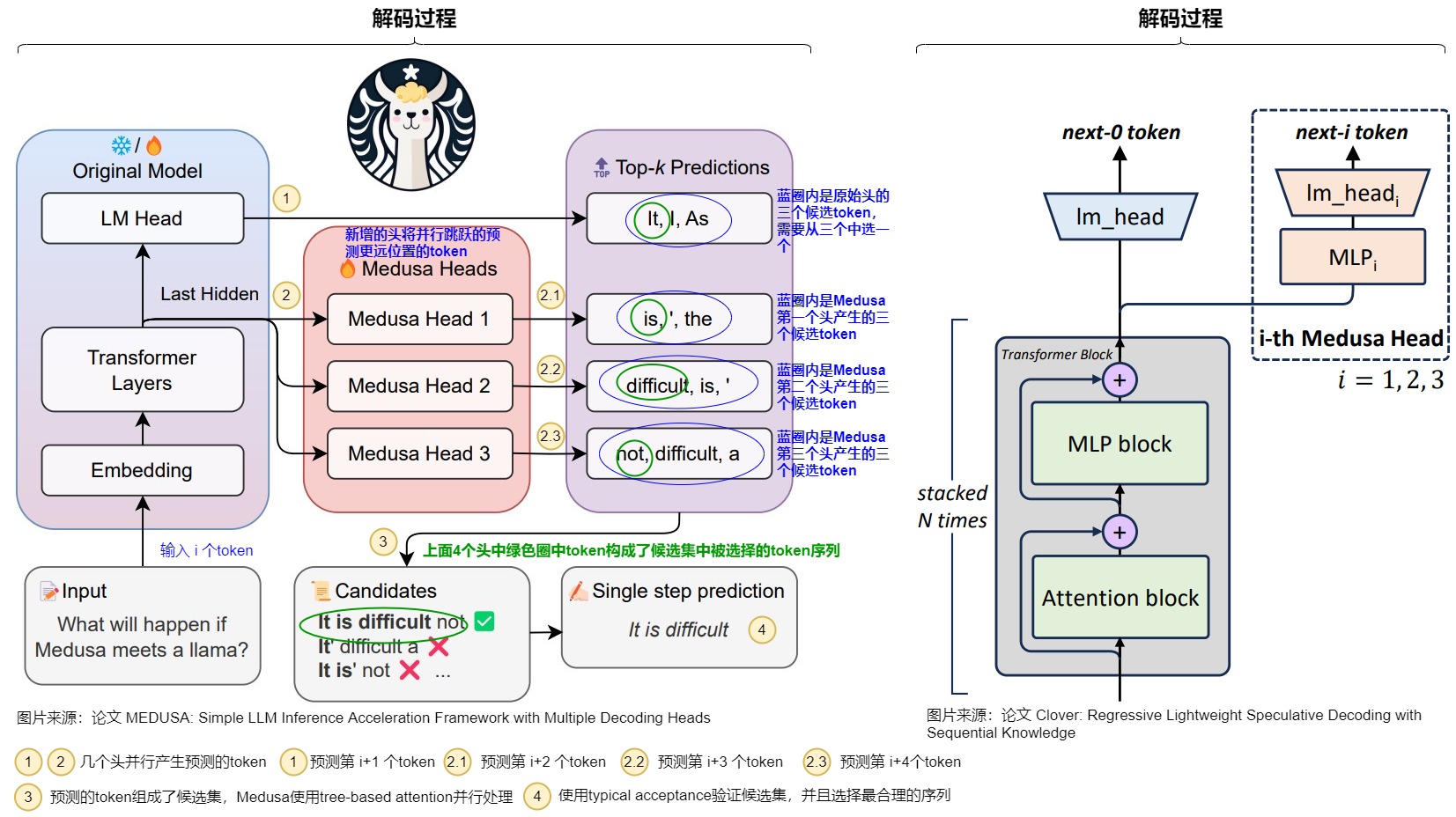
Medusa每个头预测的偏移量是不同的,第 \(k\) 个头用来预测位置 \(t+k+1\) 的输出token(\(k\) 的取值是\(1\sim K\))。原模型的解码头依然预测位置 \(t+1\) 的输出,相当于 \(k=0\)。具体而言,把原始模型在位置 \(t\) 的最后隐藏状态 \(h_t\) 接入到 \(K\) 个解码头上,对于输入token序列 \(t_0,t_1,..,t_i\),原始的head根据输入预测 \(t_{i+1}\),Medusa新增的第一个head根据输入预测 \(t_{i+2}\) 的token,也就是跳过token \(t_{i+1}\) 预测下一个未来的token。并且每个头可以指定topk个结果。这些头的预测结果构成了多个候选词汇序列,然后利用树形注意力机制同时处理这些候选序列。在每个解码步,选择最长被接受的候选序列作为最终的预测结果。这样,每步可以预测多个词汇,从而减少了总的解码步数,提高了推理速度。
如下图所示,Medusa在原始模型基础上,增加了3个额外的Head,可以并行预测出后4个token的候选。
缺点
Medusa的缺点如下:
- Medusa 新增的 lm_head 和最后一个 Transformer Block 中间只有一个 MLP,表达能力可能有限。
- Medusa 增加了模型参数量,会增加显存占用;
- Medusa 每个 head 都是独立执行的,也就是 “next next token” 预测并不会依赖上一个 “next token” 的结果,导致生成效果不佳,接受率比较低,在大 batch size 时甚至可能负优化。
- 缺乏序列依赖也可能导致低效的树剪枝算法。
- 草稿质量仍然不高,加速效果有限,并且在非贪婪解码 (non-greedy decoding) 下不能保证输出分布与目标LLM一致。
因此,后续有研究工作对此进行了改进。比如Clover重点是提供序列依赖和加入比单个 MLP 具有更强的表征能力的模块。Hydra 增加了 draft head 预测之间的关联性。Hydra++使用 base model 的输出预测概率作为知识蒸馏的教师模型输出来训练 draft head。并且类似EAGLE,Hydra++增加一个独立的 decoder layer,每个 Hydra head 除了上一个 token 本身,还添加了上一个 token 在这个 decoder layer 的 representation 作为输入。
Tree Verification
每个Medusa Head 会生成 top-k 个预测标记,然后通过计算这些预测的笛卡尔积来形成候选序列。我们可以对于每个候选序列都走一遍模型来验证,但是这样做太耗时。因此,Medusa 作者设计了一种tree attention的机制,在候选树内进行掩码操作,掩码限制某个token对前面token的注意力。同时,也要为相应地为position embedding设置正确的位置索引。因为有 tree attention 的存在,所以 Medusa 可以并行地构建、维护和验证多个候选序列。
解码路径
在Medusa中,基础版本解码采用greedy方式取Top-1 Token。Medusa增加额外的解码头之后,使用 Top-K Sampling,每一个 Head 都会输出 k 个 tokens。不同Medusa头之间预测结果不一致。\(p(t_{t+1}|t_0,...,t_i)\) 和 \(p(t_{t+2}|t_0,...,t_{i})\) 形式上是条件独立的,但是实际上 \(p_{t+2}\) 依赖 \(p_{t+1}\),不能直接取\(p(t_{t+1}|t_0,...,t_i)\)和 \(p(t_{t+2}|t_0,...,t_i)\) 最大的token作为verify阶段的输入,这样组成的句子可能会在逻辑上不一致。
因此,Medusa还引入采样topk组合作为候选序列的方式去缓解这个问题。最终把LM_head 的输出作为根节点构建出树状结构,树的深度自顶向下遍历称为解码路径(论文中叫做candidates path)。每个候选序列可以表示所构建的tree上的一条路径上所有的node(而不只是leaf node,因为tree attention验证的时候会把路径上所有token都进行验证)。
由于有\(K\) 个head,每个head选取 top-\(s_k\) 个预测输出,则所有路径可能组合为树上所有节点的总和,即\(\sum_{k=1}^K \prod_{i=1}^k s_i\)。在构建树形结构时,最简单的方法是通过笛卡尔积来获取多个解码头组成的所有可能的候选序列。
下图例子使用了Cartesian product对两个解码头的结果进行处理,获得所有候选序列。具体来说就是将每个头的top-k个词作为节点,每个头作为树的一层。图上一共存在6条解码路径,相当于 Head 1 在下一个位置生成 2 个可能的 Token(It 和 I),Head 2 在下下一个位置生成 3 个可能的 Token(is,’ 和 the),这样下一个位置和下下一个位置就有了 2 x 3 = 6 种可能的候选序列。为了区分不同的 prefix,Medusa 设置了一些冗余,例如 Head 2 的三个预测 token 均出现了两次,这是为了分别对应 It 和 I 这两个不同的 prefix。每个 token 在 tree mask 的作用下只可以看见自己的 prefix。
减枝
上图采用top-3,两个头一共有6条候选路径。如果解码头数量数量比较多,每个头给出的候选token也比较多。解码路径会随着Top-k 和头数增多急剧增加,会产生大量的候选路径,具有庞大的搜索空间。虽然增加候选序列的数量,最终接受token的命中率就会提升,但是验证更多候选序列也会带来额外的计算消耗。那么新的问题是:
- 如何能减少候选解码路径?
- 如何能在候选解码路径中,得到最优解码路径?
直观上来说,那些由不同头部的topk预测组成的候选结果可能具有不同的准确率。应该优先选择那些更准确的预测,从而构建一个更有效的树,而不需要使用所有可能的排列组合。Medusa 通过在校准数据集上统计每个解码头的 top-k 预测的准确率,然后贪婪地选择那些能够最大化期望接受长度的节点,将它们加入到树中。这样可以在相同的节点总数下,获得更高的加速比。其实,此方法本质上就是用剪枝来加速,剪去每个head中top-\(s_k\)的若干个。
具体来说,我们可以使用一个calibration dataset(比如Alpaca-eval dataset)来获取不同解码头给出的各个token的准确率:把第 \(k\) 个解码头给出的第 \(i\) 个token的准确率记为 \(a^{(i)}_k\)。假设各个token的准确率之间是独立的,那么一个由 \([i_1,i_2,\cdots,i_k]\) 构成的候选序列的准确率可以写作 \(\prod_{j=1}^ka_j^{(i_j)}\)。
我们用 \(I\) 表示候选序列的集合,那么集合里的候选序列的接受长度期望(expectation of acceptance length)就表示为:
在构建tree的时候,Medusa在选择加入节点时会贪心的优先加入当前有最大准确率的候选序列,直到tree的节点数量达到接受长度的期望值上限,这样能最大化expectation of acceptance length,也就能最大化acceleration rate。这是一种手工设计的稀疏树结构,越靠前的节点,有更多的子节点路径。即,把所有位置组合穷举,然后选取前𝑁个组合作为固定考察的可能,剩余的剪枝去掉。
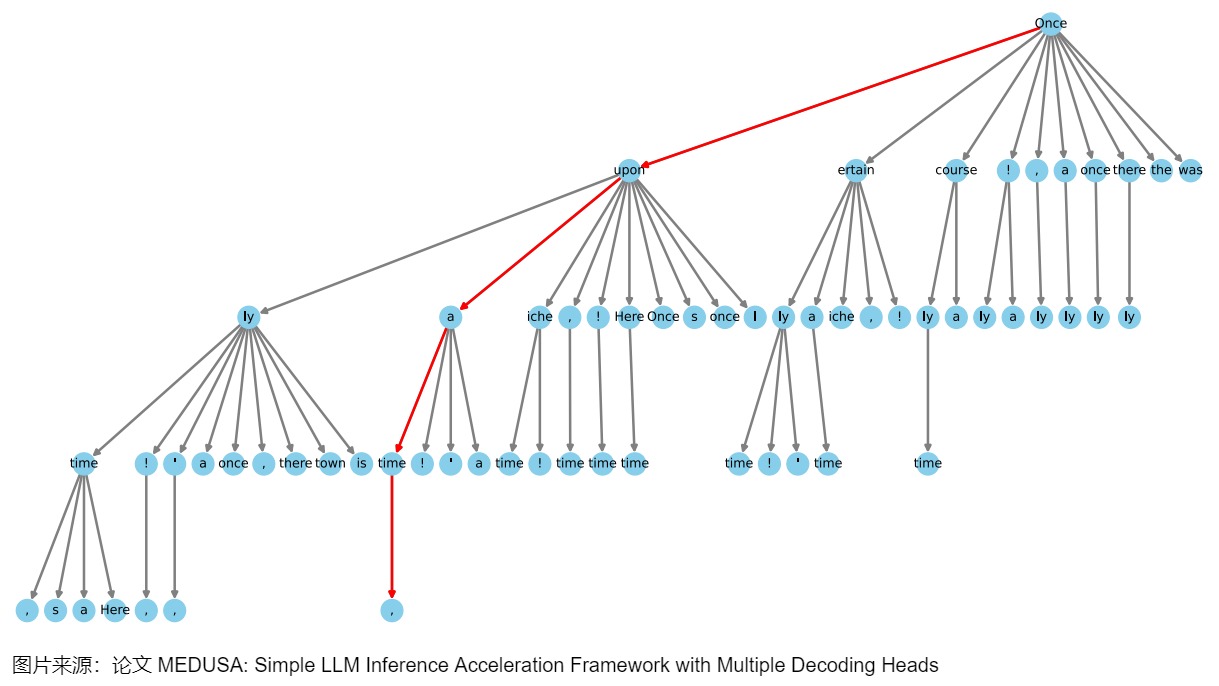
MEDUSA-2 Vicuna-7B模型的一个稀疏树示例如下图所示。这个树结构延伸了四个层次,表明有四个MEDUSA头参与了计算。该树最初通过笛卡尔积方法生成,随后根据每个MEDUSA头在Alpaca-eval数据集上测量的前 \(k\) 个预测的统计期望值进行修剪。树向左倾斜在视觉上代表了算法倾向于使用更高准确率的token,每个节点表示MEDUSA头部的top-k预测中的一个token,边显示了它们之间的连接,红线突出显示了正确预测未来token的路径。这样就将1000个路径的树优化到只有42条路径,而且,这里的路径可以提前结束,不要求一定要遍历到最后一层。
Typical Acceptance
在投机解码中,拒绝采样是指从草稿模型的输出中随机采样一个 token 序列,然后使用原始模型来验证是否接受。如果验证失败,就重新采样,直至找到一个合适的 token 序列。而在实际应用中,往往不需要完全匹配原始模型的分布,只要保证输出的质量和多样性即可,这样可以获取更加合理的候选token,也可以加速解码过程。因此 Medusa 使用了典型接受方案。该方案是基于原始模型预测的概率,使用温度来设定一个阈值,根据这个阈值来决定是否接受候选的 token。如果候选 token 的概率超过了阈值,就认为这个 token 是「典型」的,应该接受。
常见采用方法
LLM模型的输出是在词表上的概率分布,采样策略直接决定了我们得到怎么样的输出效果。有时候我们希望得到完全确定的结果,有时候希望得到更加丰富有趣的结果。
确定性采样的输出结果是确定性的,本质上是搜索过程,典型两种方法如下。
- Greedy Search。每次选取概率最高的token输出。
-
Beam Search。维护beam的大小为k,对当前beam中的所有path做下个token的展开,选取累积概率最高的前k个path,作为新的beam,以此类推。
概率性采样会基于概率分布做采样,常见的有以下3种 -
Multinomial采样。直接基于概率分布做纯随机采样,容易采到极低概率的词。
- Top-k采样。在概率排名前k的候选集中做随机采样,注意采样前做重新归一化。
- Top-p采样。也叫Nucleus采样,先对输出概率做从大到小的排序,然后在累积概率达到p的这些候选集中做随机采样,同样需要做重新归一化。
基于采样的方法中往往有一个温度参数,温度越高采样的多样性越高,适用于创意生成的场景,比如写作文。
Typical Acceptance
推测解码中,作者采用拒绝采样来产生与原始模型的分布一致的不同输出。然而,后续的研究工作发现,随着采样温度的升高,这种采样策略会导致效率降低。比如,draft模型与target模型一样好,他们的分布完美地对齐。在这种状态下,我们应该接受draft模型所有输出。然而,因为草稿模型与原始模型进行独立采样,temperature提升一般对应更强的creativity特性,draft model所选择的候选token的多样性就增大,也就降低了命中原模型token被接受的概率,从而导致并行解码长度很短。而此时,贪婪解码会接受草稿模型的所有输出,反而会最大化效率。
但是这种特性并不合理。因为在现实场景中,语言模型的采样通常用于生成不同的响应,而温度参数仅用于调节响应的"创造力"。因此,较高的温度应该会导致原始模型有更多机会接受草稿模型的输出,但不一定要匹配原始模型的分布。那么,为什么不只是专注于接受似乎合理(plausible)的候选token呢?
MEDUSA认为既然采样就是追求创造性,候选序列的分布没有必要完全匹配原模型的分布。我们要做的应该是选出typical的候选,也就是,只要候选序列不是极不可能的结果,就可以被接受。直观理解是我们在LLM解码过程,不需要太确定的词,也不能有太超出预期的词,这样就能保证我们能得到丰富且避免重复生成的词汇。
于是,Medusa从截断采样(Truncation Sampling)工作中汲取灵感,旨在扩大选择原始模型可能接受的候选项。Medusa 根据原始模型的预测概率设定一个阈值,如果候选token超过了这个阈值,就会被接受该token 及其 prefix,并在这些token中做Greedy采样选择top-k。而这个阈值由原始模型的预测概率相关。
具体来说,作者采取hard threshold和entropy-dependent threshold的最小值来决定是否像在truncation sampling中那样接受一个候选token。这确保了在解码过程中选择有意义的token和合理的延续。作者总是使用Greedy Decoding接受第一个token,确保每一步至少生成一个token。最后选择被接受的解码长度最长的候选序列作为最终结果。这种方法的好处是其适应性:如果你将采样温度设为零,它就简单地回归到最高效的形式Greedy Search。当你提高温度时,此方法变得更加高效,允许更长的接受序列。
- 当概率分布中有个别token的概率很高,这时熵小, exp(−𝐻(⋅)) 大,token接受的条件更严格。
- 当概率分布中每个token的概率比较平均时,熵大, exp(−𝐻(⋅)) 小,token接受的条件宽松一些。
