分布变换

通常我们会拿VAE跟GAN比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量 \(Z\) 生成目标数据 \(X\) 的模型，但是实现上有所不同。更准确地讲，它们是假设了 \(Z\) 服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型 \(X=g(Z)\)，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。

生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式

那现在假设 \(Z\) 服从标准的正态分布，那么我就可以从中采样得到若干个 \(Z_1, Z_2, \dots, Z_n\)，然后对它做变换得到 \(\hat{X}_1 = g(Z_1),\hat{X}_2 = g(Z_2),\dots,\hat{X}_n = g(Z_n)\)，我们怎么判断这个通过 \(g\) 构造出来的数据集，它的分布跟我们目标的数据集分布是不是一样的呢？有读者说不是有KL散度吗？当然不行，因为KL散度是根据两个概率分布的表达式来算它们的相似度的，然而目前我们并不知道它们的概率分布的表达式，我们只有一批从构造的分布采样而来的数据 \(\{\hat{X}_1,\hat{X}_2,\dots,\hat{X}_n\}\) ，还有一批从真实的分布采样而来的数据 \(\{X_1,X_2,\dots,X_n\}\)（也就是我们希望生成的训练集）。我们只有样本本身，没有分布表达式，当然也就没有方法算KL散度。

虽然遇到困难，但还是要想办法解决的。GAN的思路很直接粗犷：既然没有合适的度量，那我干脆把这个度量也用神经网络训练出来吧。就这样，WGAN就诞生了，详细过程请参考《互怼的艺术：从零直达WGAN-GP》。而VAE则使用了一个精致迂回的技巧。

VAE慢谈

这一部分我们先回顾一般教程是怎么介绍VAE的，然后再探究有什么问题，接着就自然地发现了VAE真正的面目。

经典回顾

首先我们有一批数据样本 \(\{X_1,\dots,X_n\}\)，其整体用 \(X\) 来描述，我们本想根据 \(\{X_1,\dots,X_n\}\) 得到 \(X\) 的分布 \(p(X)\)，如果能得到的话，那我直接根据 \(p(X)\) 来采样，就可以得到所有可能的 \(X\) 了（包括 \(\{X_1,\dots,X_n\}\) 以外的），这是一个终极理想的生成模型了。当然，这个理想很难实现，于是我们将分布改一改

\[p(X)=\sum_Z p(X|Z)p(Z)\tag{1} \]

这里我们就不区分求和还是求积分了，意思对了就行。此时 \(p(X|Z)\) 就描述了一个由 \(Z\) 来生成 \(X\) 的模型，而我们假设 \(Z\) 服从标准正态分布，也就是 \(p(Z)=\mathcal{N}(0,I)\)。

如果这个理想能实现，那么我们就可以先从标准正态分布中采样一个\(Z\)，然后根据 \(Z\) 来算一个 \(X\)，也是一个很棒的生成模型。

接下来就是结合自编码器来实现重构，保证有效信息没有丢失，再加上一系列的推导，最后把模型实现。框架的示意图如下：

看出了什么问题了吗？如果像这个图的话，我们其实完全不清楚：究竟经过重新采样出来的 \(Z_k\)，是不是还对应着原来的 \(X_k\)，所以我们如果直接最小化 \(\mathcal{D}(\hat{X}_k,X_k)^2\)（这里 \(\mathcal{D}\) 代表某种距离函数）是很不科学的，而事实上你看代码也会发现根本不是这样实现的。也就是说，很多教程说了一大通头头是道的话，然后写代码时却不是按照所写的文字来写，可是他们也不觉得这样会有矛盾～

VAE初现

其实，在整个VAE模型中，我们并没有去使用 \(p(Z)\)（隐变量空间的分布）是正态分布的假设，我们用的是假设 \(p(Z|X)\)（后验分布）是正态分布！！

具体来说，给定一个真实样本 \(X_k\)，我们假设存在一个专属于 \(X_k\) 的分布 \(p(Z|X_k)\)（学名叫后验分布），并进一步假设这个分布是（独立的、多元的）正态分布。为什么要强调“专属”呢？因为我们后面要训练一个生成器 \(X=g(Z)\)，希望能够把从分布 \(p(Z|X_k)\) 采样出来的一个 \(Z_k\) 还原为 \(X_k\)。如果假设 \(p(Z)\) 是正态分布，然后从 \(p(Z)\) 中采样一个 \(Z\)，那么我们怎么知道这个 \(Z\) 对应于哪个真实的 \(X\) 呢？现在 \(p(Z|X_k)\) 专属于 \(X_k\)，我们有理由说从这个分布采样出来的 \(Z\) 应该要还原到 \(X_k\) 中去。

事实上，在论文《Auto-Encoding Variational Bayes》的应用部分，也特别强调了这一点：

In this case, we can let the
variational approximate posterior be a multivariate Gaussian with a diagonal covariance structure:
\[\log q_{\phi}(\boldsymbol{z}|\boldsymbol{x}^{(i)}) = \log \mathcal{N}(\boldsymbol{z} ;\boldsymbol{\mu}^{(i)},\boldsymbol{\sigma}^{2(i)}\boldsymbol{I})\]

（注：这里是直接摘录原论文，本文所用的符号跟原论文不尽一致，望读者不会混淆。）

论文中的公式是实现整个模型的关键，不知道为什么很多教程在介绍VAE时都没有把它凸显出来。尽管论文也提到 \(p(Z)\) 是标准正态分布，然而那其实并不是本质重要的。

回到本文，这时候每一个 \(X_k\) 都配上了一个专属的正态分布，才方便后面的生成器做还原。但这样有多少个 \(X\) 就有多少个正态分布了。我们知道正态分布有两组参数：均值 \(\mu\) 和方差 \(\sigma^2\)（多元的话，它们都是向量），那我怎么找出专属于 \(X_k\) 的正态分布 \(p(Z|X_k)\) 的均值和方差呢？好像并没有什么直接的思路。那好吧，那我就用神经网络来拟合出来吧！这就是神经网络时代的哲学：难算的我们都用神经网络来拟合，在WGAN那里我们已经体验过一次了，现在再次体验到了。

于是我们构建两个神经网络 \(\mu_k = f_1(X_k),\log \sigma_k^2 = f_2(X_k)\) 来算它们了。我们选择拟合 \(\log \sigma_k^2\) 而不是直接拟合 \(\sigma_k^2\)，是因为 \(\sigma_k^2\) 总是非负的，需要加激活函数处理，而拟合 \(\log \sigma_k^2\) 不需要加激活函数，因为它可正可负。到这里，我能知道专属于 \(X_k\) 的均值和方差了，也就知道它的正态分布长什么样了，然后从这个专属分布中采样一个 \(Z_k\) 出来，然后经过一个生成器得到 \(\hat{X}_k=g(Z_k)\)，现在我们可以放心地最小化 \(\mathcal{D}(\hat{X}_k,X_k)^2\)，因为 \(Z_k\) 是从专属 \(X_k\) 的分布中采样出来的，这个生成器应该要把开始的 \(X_k\) 还原回来。于是可以画出VAE的示意图

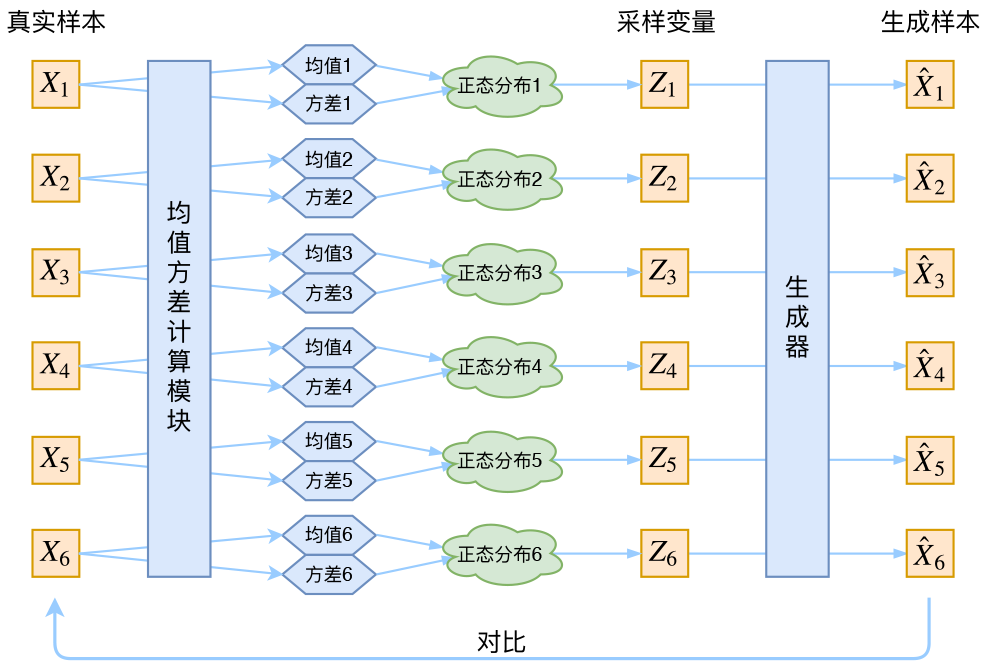
分布标准化

让我们来思考一下，根据上图的训练过程，最终会得到什么结果。

首先，我们希望重构 \(X\)，也就是最小化 \(\mathcal{D}(\hat{X}_k,X_k)^2\) ，但是这个重构过程受到噪声的影响，因为\(Z_k\) 是通过重新采样过的，不是直接由encoder算出来的。显然噪声会增加重构的难度，不过好在这个噪声强度（也就是方差）通过一个神经网络算出来的，所以最终模型为了重构得更好，肯定会想尽办法让方差为0。而方差为0的话，也就没有随机性了，所以不管怎么采样其实都只是得到确定的结果（也就是均值），只拟合一个当然比拟合多个要容易，而均值是通过另外一个神经网络算出来的。

说白了，模型会慢慢退化成普通的AutoEncoder，噪声不再起作用。

这样不就白费力气了吗？说好的生成模型呢？

别急别急，其实VAE还让所有的 \(p(Z|X)\) 都向标准正态分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。怎么理解“保证了生成能力”呢？如果所有的 \(p(Z|X)\) 都很接近标准正态分布 \(\mathcal{N}(0,I)\)，那么根据定义

\[p(Z)=\sum_X p(Z|X)p(X)=\sum_X \mathcal{N}(0,I)p(X)=\mathcal{N}(0,I) \sum_X p(X) = \mathcal{N}(0,I)\tag{2}\]

这样我们就能达到我们的先验假设：\(p(Z)\) 是标准正态分布。然后我们就可以放心地从 \(\mathcal{N}(0,I)\) 中采样来生成图像了。

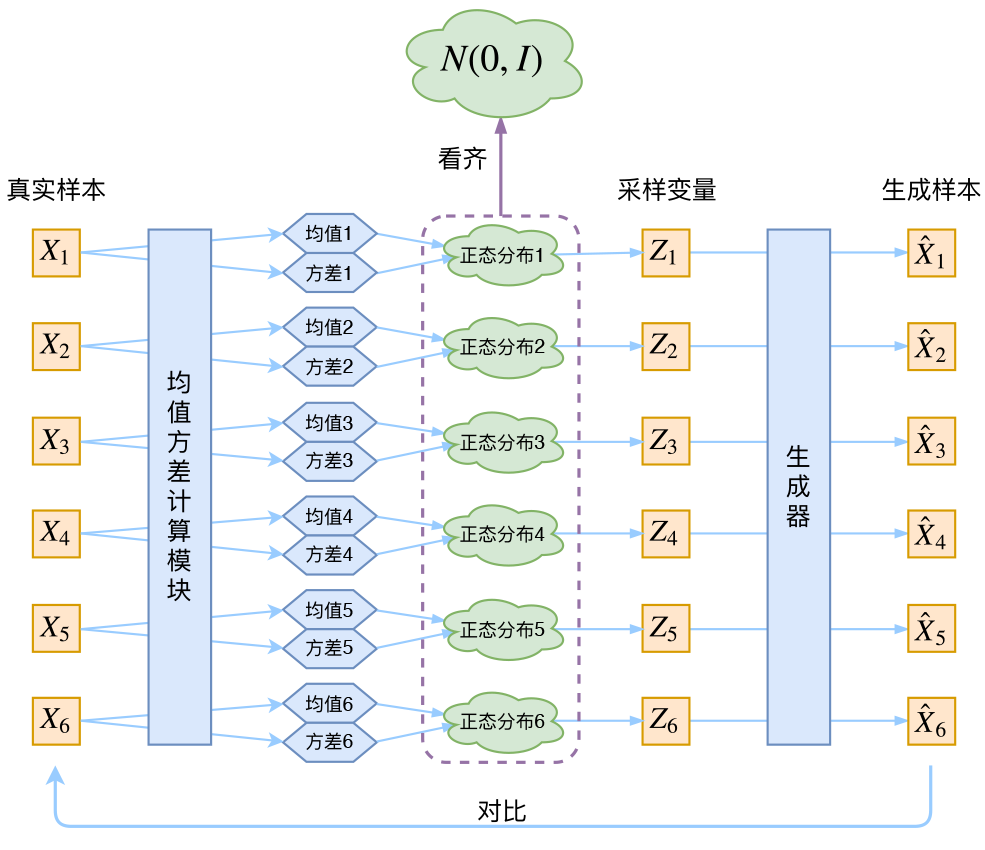
那怎么让所有的 \(p(Z|X)\) 都向 \(\mathcal{N}(0,I)\) 看齐呢？如果没有外部知识的话，其实最直接的方法应该是在重构误差的基础上中加入额外的loss：

\[\mathcal{L}_{\mu}=\Vert f_1(X_k)\Vert^2\quad \text{和}\quad \mathcal{L}_{\sigma^2}=\Vert f_2(X_k)\Vert^2 \tag{3}\]

因为它们分别代表了均值 \(\mu_k\) 和方差的对数 \(\log\sigma_k^2\)，达到 \(\mathcal{N}(0,I)\) 就是希望二者尽量接近于0了。不过，这又会面临着这两个损失的比例要怎么选取的问题，选取得不好，生成的图像会比较模糊。所以，原论文直接算了一般（各分量独立的）正态分布与标准正态分布的KL散度\(KL\Big(N(\mu,\sigma^2)\Big\Vert N(0,I)\Big)\) 作为这个额外的loss，计算结果为

\[\mathcal{L}_{\mu,\sigma^2}=\frac{1}{2} \sum_{i=1}^d \Big(\mu_{(i)}^2 + \sigma_{(i)}^2 - \log \sigma_{(i)}^2 - 1\Big)\tag{4}\]

这里的 \(d\) 是隐变量 \(Z\) 的维度，而 \(\mu_{(i)}\) 和 \(\sigma_{(i)}^2\) 分别代表一般正态分布的均值向量和方差向量的第 \(i\) 个分量。直接用这个式子做补充loss，就不用考虑均值损失和方差损失的相对比例问题了。显然，这个loss也可以分两部分理解：

\[\begin{aligned}&\mathcal{L}_{\mu,\sigma^2}=\mathcal{L}_{\mu} + \mathcal{L}_{\sigma^2}\\ &\mathcal{L}_{\mu}=\frac{1}{2} \sum_{i=1}^d \mu_{(i)}^2=\frac{1}{2}\Vert f_1(X)\Vert^2\\ &\mathcal{L}_{\sigma^2}=\frac{1}{2} \sum_{i=1}^d\Big(\sigma_{(i)}^2 - \log \sigma_{(i)}^2 - 1\Big)\end{aligned}\tag{5}\]

💡 推导
由于我们考虑的是各分量独立的多元正态分布，因此只需要推导一元正态分布的情形即可，根据定义我们可以写出
根据定义我们可以写出
\[\begin{aligned}&KL\Big(N(\mu,\sigma^2)\Big\Vert N(0,1)\Big)\\ =&\int \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2} \left(\log \frac{e^{-(x-\mu)^2/2\sigma^2}/\sqrt{2\pi\sigma^2}}{e^{-x^2/2}/\sqrt{2\pi}}\right)dx\\ =&\int \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2} \log \left\{\frac{1}{\sqrt{\sigma^2}}\exp\left\{\frac{1}{2}\big[x^2-(x-\mu)^2/\sigma^2\big]\right\} \right\}dx\\ =&\frac{1}{2}\int \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2} \Big[-\log \sigma^2+x^2-(x-\mu)^2/\sigma^2 \Big] dx\end{aligned}\]

整个结果分为三项积分，第一项实际上就是 \(-\log \sigma^2\) 乘以概率密度的积分（也就是1），所以结果是\(-\log \sigma^2\)；第二项实际是正态分布的二阶矩，熟悉正态分布的朋友应该都清楚正态分布的二阶矩为 \(\mu^2+\sigma^2\)；而根据定义，第三项实际上就是“-方差除以方差=-1”。所以总结果就是
\[KL\Big(N(\mu,\sigma^2)\Big\Vert N(0,1)\Big)=\frac{1}{2}\Big(-\log \sigma^2+\mu^2+\sigma^2-1\Big)\]

重参数技巧

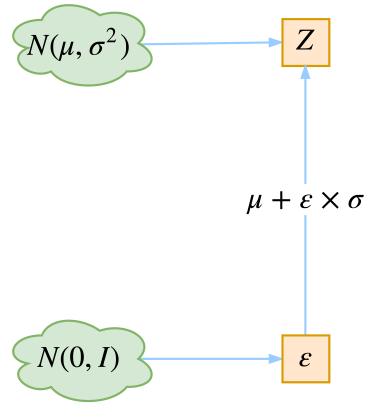
最后是实现模型的一个技巧，英文名是reparameterization trick，我这里叫它做重参数吧。其实很简单，就是我们要从 \(p(Z|X_k)\) 中采样一个 \(Z_k\) 出来，尽管我们知道了 \(p(Z|X_k)\) 是正态分布，但是均值方差都是靠模型算出来的，我们要靠这个过程反过来优化均值方差的模型，但是“采样”这个操作是不可导的，而采样的结果是可导的。我们利用

\[\begin{aligned}&\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(z-\mu)^2}{2\sigma^2}\right)dz \\ =& \frac{1}{\sqrt{2\pi}}\exp\left[-\frac{1}{2}\left(\frac{z-\mu}{\sigma}\right)^2\right]d\left(\frac{z-\mu}{\sigma}\right)\end{aligned}\tag{6}\]

这说明 \((z-\mu)/\sigma=\varepsilon\) 是服从均值为0、方差为1的标准正态分布的，要同时把 \(dz\) 考虑进去，是因为乘上\(dz\)才算是概率，去掉 \(dz\) 是概率密度而不是概率。这时候我们得到：

💡 从\(\mathcal{N}(\mu,\sigma^2)\)中采样一个\(Z\)，相当于从\(\mathcal{N}(0,I)\)中采样一个\(\varepsilon\)，然后让 \(Z=\mu + \varepsilon \times \sigma\)。

于是，我们将从 \(\mathcal{N}(\mu,\sigma^2)\) 采样变成了从 \(\mathcal{N}(0,I)\) 中采样，然后通过参数变换得到从 \(\mathcal{N}(\mu,\sigma^2)\) 中采样的结果。这样一来，“采样”这个操作就不用参与梯度下降了，改为采样的结果参与，使得整个模型可训练了。

具体怎么实现，大家把上述文字对照着代码看一下，一下子就明白了～

class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()

        self.fc1 = nn.Linear(784, 400)
        self.fc21 = nn.Linear(400, 20)
        self.fc22 = nn.Linear(400, 20)
        self.fc3 = nn.Linear(20, 400)
        self.fc4 = nn.Linear(400, 784)

    def encode(self, x):
        h1 = F.relu(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)

    def reparametrize(self, mu, logvar):
        std = logvar.mul(0.5).exp_()
        if torch.cuda.is_available():
            eps = torch.cuda.FloatTensor(std.size()).normal_()
        else:
            eps = torch.FloatTensor(std.size()).normal_()
        return eps.mul(std).add_(mu)

    def decode(self, z):
        h3 = F.relu(self.fc3(z))
        return F.sigmoid(self.fc4(h3))

    def forward(self, x):
        mu, logvar = self.encode(x)
        z = self.reparametrize(mu, logvar)
        return self.decode(z), mu, logvar

后续分析

即便把上面的所有内容都搞清楚了，面对VAE，我们可能还存有很多疑问。

本质是什么

VAE的本质是什么？VAE虽然也称是AE（AutoEncoder）的一种，但它的做法（或者说它对网络的诠释）是别具一格的。在VAE中，它的Encoder有两个，一个用来计算均值，一个用来计算方差，这已经让人意外了：Encoder不是用来Encode的，是用来算均值和方差的，这真是大新闻了，还有均值和方差不都是统计量吗，怎么是用神经网络来算的？

事实上，我觉得VAE从让普通人望而生畏的变分和贝叶斯理论出发，最后落地到一个具体的模型中，虽然走了比较长的一段路，但最终的模型其实是很接地气的：它本质上就是在我们常规的自编码器的基础上，对encoder的结果（在VAE中对应着计算均值的网络）加上了“高斯噪声”，使得结果decoder能够对噪声有鲁棒性；而那个额外的KL loss（目的是让均值为0，方差为1），事实上就是相当于对encoder的一个正则项，希望encoder出来的东西有零均值。

那另外一个encoder（对应着计算方差的网络）的作用呢？它是用来动态调节噪声的强度的。直觉上来想，当decoder还没有训练好时（重构误差远大于KL loss），就会适当降低噪声（KL loss增加），使得拟合起来容易一些（重构误差开始下降）；反之，如果decoder训练得还不错时（重构误差小于KL loss），这时候噪声就会增加（KL loss减少），使得拟合更加困难了（重构误差又开始增加），这时候decoder就要想办法提高它的生成能力了。

说白了，重构的过程是希望没噪声的，而KL loss则希望有高斯噪声的，两者是对立的。所以，VAE跟GAN一样，内部其实是包含了一个对抗的过程，只不过它们两者是混合起来，共同进化的。从这个角度看，VAE的思想似乎还高明一些，因为在GAN中，造假者在进化时，鉴别者是安然不动的，反之亦然。当然，这只是一个侧面，不能说明VAE就比GAN好。GAN真正高明的地方是：它连度量都直接训练出来了，而且这个度量往往比我们人工想的要好（然而GAN本身也有各种问题，这就不展开了）。

从这个讨论中，我们也可以看出，当然，每个 \(p(Z|X)\) 是不可能完全精确等于标准正态分布，否则\(p(Z|X)\) 就相当于跟 \(X\) 无关了，重构效果将会极差。最终的结果就会是，\(p(Z|X)\) 保留了一定的\(X\)信息，重构效果也还可以，并且(2)近似成立，所以同时保留着生成能力。

正态分布?

对于 \(p(Z|X)\) 的分布，读者可能会有疑惑：是不是必须选择正态分布？可以选择均匀分布吗？

估计不大可行，这还是因为KL散度的计算公式：

\[KL\Big(p(x)\Big\Vert q(x)\Big) = \int p(x) \ln \frac{p(x)}{q(x)}dx\tag{7}\]

要是在某个区域中 \(p(x)\neq 0\) 而 \(q(x)=0\) 的话，那么KL散度就无穷大了。对于正态分布来说，所有点的概率密度都是非负的，因此不存在这个问题。但对于均匀分布来说，只要两个分布不一致，那么就必然存在 \(p(x)\neq 0\)而\(q(x)=0\)的区间，因此KL散度会无穷大。当然，写代码时我们会防止这种除零错误，但依然避免不了KL loss占比很大，因此模型会迅速降低KL loss，也就是后验分布 \(p(Z|X)\) 迅速趋于先验分布 \(p(Z)\)，而噪声和重构无法起到对抗作用。这又回到我们开始说的，无法区分哪个\(z\)对应哪个\(x\)了。

当然，非得要用均匀分布也不是不可能，就是算好两个均匀分布的KL散度，然后做好除零错误处理，加大重构loss的权重，等等～但这样就显得太丑陋了。

变分在哪里

还有一个有意思（但不大重要）的问题是：VAE叫做“变分自编码器”，它跟变分法有什么联系？在VAE的论文和相关解读中，好像也没看到变分法的存在呀？

呃～其实如果读者已经承认了KL散度的话，那VAE好像真的跟变分没多大关系了～因为理论上对于KL散度(7)我们要证明：

💡 固定概率分布 \(p(x)\)（或\(q(x)\)）的情况下，对于任意的概率分布\(q(x)\)（或\(p(x)\)），都有\(KL\Big(p(x)\Big\Vert q(x)\Big)\geq 0\)，而且只有当 \(p(x)=q(x)\) 时才等于零。

因为\(KL\Big(p(x)\Big\Vert q(x)\Big)\) 实际上是一个泛函，要对泛函求极值就要用到变分法，当然，这里的变分法只是普通微积分的平行推广，还没涉及到真正复杂的变分法。而VAE的变分下界，是直接基于KL散度就得到的。所以直接承认了KL散度的话，就没有变分的什么事了。

一句话，VAE的名字中“变分”，是因为它的推导过程用到了KL散度及其性质。

条件VAE

最后，因为目前的VAE是无监督训练的，因此很自然想到：如果有标签数据，那么能不能把标签信息加进去辅助生成样本呢？这个问题的意图，往往是希望能够实现控制某个变量来实现生成某一类图像。当然，这是肯定可以的，我们把这种情况叫做Conditional VAE，或者叫CVAE。（相应地，在GAN中我们也有个CGAN。）

但是，CVAE不是一个特定的模型，而是一类模型，总之就是把标签信息融入到VAE中的方式有很多，目的也不一样。这里基于前面的讨论，给出一种非常简单的VAE。

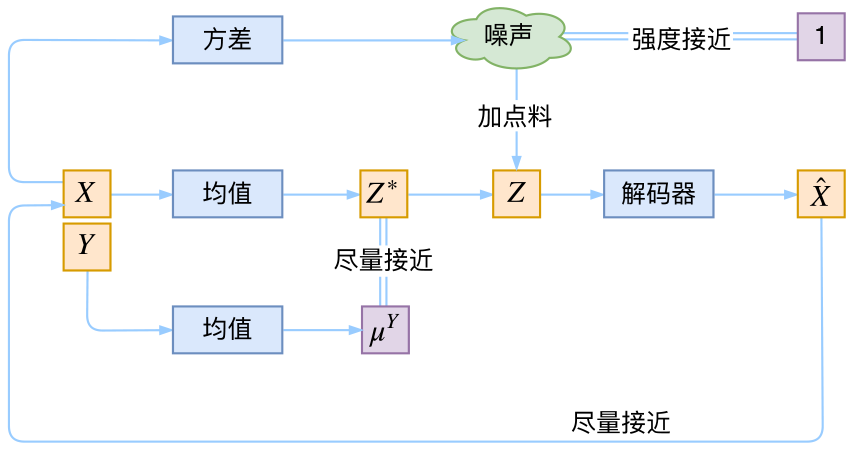
在前面的讨论中，我们希望 \(X\) 经过编码后，\(Z\) 的分布都具有零均值和单位方差，这个“希望”是通过加入了 KL loss 来实现的。如果现在多了类别信息\(Y\)，我们可以希望同一个类的样本都有一个专属的均值 \(\mu^Y\)（方差不变，还是单位方差），这个 \(\mu^Y\) 让模型自己训练出来。这样的话，有多少个类就有多少个正态分布，而在生成的时候，我们就可以通过控制均值来控制生成图像的类别。事实上，这样可能也是在VAE的基础上加入最少的代码来实现CVAE的方案了，因为这个“新希望”也只需通过修改KL loss实现：

\[\mathcal{L}_{\mu,\sigma^2}=\frac{1}{2} \sum_{i=1}^d\Big[\big(\mu_{(i)}-\mu^Y_{(i)}\big)^2 + \sigma_{(i)}^2 - \log \sigma_{(i)}^2 - 1\Big]\tag{8}\]

下图显示这个简单的CVAE是有一定的效果的，不过因为encoder和decoder都比较简单（纯MLP），所以控制生成的效果不尽完美。更完备的CVAE请读者自行学习了，最近还出来了CVAE与GAN结合的工作CVAE-GAN，模型套路千变万化啊。

用这个cvae控制生成数字9，可以发现生成了多种样式的9，并且慢慢向7过渡，所以初步观察这种cvae是有效的

从贝叶斯观点出发

准备

在进入对VAE的描述之前，我觉得有必要把一些概念性的内容讲一下。

数值计算vs采样计算

对于不是很熟悉概率统计的读者，容易混淆的两个概念应该是数值计算和采样计算。比如已知概率密度函数 \(p(x)\)，那么 \(x\) 的期望也就定义为

\[ \mathbb{E}[x] = \int x p(x)dx\tag{9}\]

如果要对它进行数值计算，也就是数值积分，那么可以选若干个有代表性的点 \(x_0 < x_1 < x_2 < \dots < x_n\)，然后得到

\[\mathbb{E}[x] \approx \frac{1}{x_n - x_0}\sum_{i=1}^n x_i p(x_i) \left(x_i - x_{i-1}\right)\tag{10}\]

这里不讨论“有代表性”是什么意思，也不讨论提高数值计算精度的方法。这样写出来，是为了跟采样计算对比。如果从p(x)中采样若干个点\(x_1,x_2,\dots,x_n\)，那么我们有

\[\mathbb{E}[x] \approx \frac{1}{n}\sum_{i=1}^n x_i,\quad x_i \sim p(x)\tag{11}\]

我们可以比较(10)跟(11)，它们的主要区别是(10)中包含了概率的计算而(11)中仅有\(x\) 的计算，这是因为在(11)中 \(x_i\) 是从 p(x) 中依概率采样出来的，概率大的 \(x_i\) 出现的次数也多，所以可以说采样的结果已经包含了\(p(x)\)在里边，就不用再乘以 \(p(x_i)\) 了。

更一般地，我们可以写出

\[\mathbb{E}_{x\sim p(x)}[f(x)] = \int f(x)p(x)dx \approx \frac{1}{n}\sum_{i=1}^n f(x_i),\quad x_i\sim p(x)\tag{12}\]

这就是蒙特卡洛模拟的基础。

KL散度及变分

我们通常用KL散度来度量两个概率分布 \(p(x)\) 和 \(q(x)\) 之间的差异，定义为

\[KL\Big(p(x)\Big\Vert q(x)\Big) = \int p(x)\ln \frac{p(x)}{q(x)} dx=\mathbb{E}_{x\sim p(x)}\left[\ln \frac{p(x)}{q(x)}\right]\tag{13}\]

KL散度的主要性质是非负性，如果固定 \(p(x)\)，那么 \(KL\Big(p(x)\Big\Vert q(x)\Big)=0 \Leftrightarrow p(x)=q(x)\)；如果固定 \(q(x)\)，同样有 \(KL\Big(p(x)\Big\Vert q(x)\Big)=0 \Leftrightarrow p(x)=q(x)\)，也就是不管固定哪一个，最小化KL散度的结果都是两者尽可能相等。这一点的严格证明要用到变分法，而事实上VAE中的V（变分）就是因为VAE的推导就是因为用到了KL散度（进而也包含了变分法）。

当然，KL散度有一个比较明显的问题，就是当 \(q(x)\) 在某个区域等于0，而p(x)在该区域不等于0，那么KL散度就出现无穷大。这是KL散度的固有问题，我们只能想办法规避它，比如隐变量的先验分布我们用高斯分布而不是均匀分布，原因便在此，这一点我们在前文中也提到过了。

顺便说点题外话，度量两个概率分布之间的差异只有KL散度吗？当然不是，我们可以看维基百科的Statistical Distance一节，里边介绍了不少分布距离，比如有一个很漂亮的度量，我们称之为巴氏距离（Bhattacharyya distance），定义为

\[D_B\Big(p(x), q(x)\Big)=-\ln\int \sqrt{p(x)q(x)} dx\tag{14}\]

这个距离不仅对称，还没有KL散度的无穷大问题。然而我们还是选用KL散度，因为我们不仅要理论上的漂亮，还要实践上的可行，KL散度可以写成期望的形式，这允许我们对其进行采样计算，相反，巴氏距离就没那么容易了，读者要是想把下面计算过程中的KL散度替换成巴氏距离，就会发现寸步难行了。

框架

这里通过直接对联合分布进行近似的方式，简明快捷地给出了VAE的理论框架。

直面联合分布

出发点依然没变，这里再重述一下。首先我们有一批数据样本 \(\{x_1,\dots,x_n\}\)，其整体用 \(x\) 来描述，我们希望借助隐变量 \(z\) 描述 \(x\) 的分布 \(\tilde{p}(x)\)：

\[q(x)=\int q(x|z)q(z)dz,\quad q(x,z) = q(x|z)q(z)\tag{15}\]

这里 \(q(z)\) 是先验分布（标准正态分布），目的是希望 \(q(x)\) 能逼近 \(\tilde{p}(x)\)。这样（理论上）我们既描述了 \(\tilde{p}(x)\)，又得到了生成模型 \(q(x|z)\)，一举两得。

接下来就是利用KL散度进行近似。但我一直搞不明白的是，为什么从原作《Auto-Encoding Variational Bayes》开始，VAE的教程就聚焦于后验分布\(p(z|x)\)的描述？也许是受了EM算法的影响，这个问题上不能应用EM算法，就是因为后验分布\(p(z|x)\)难以计算，所以VAE的作者就聚焦于\(p(z|x)\)的推导。

但事实上，直接来对 \(p(x,z)\) 进行近似是最为干脆的。具体来说，定义 \(p(x,z)=\tilde{p}(x)p(z|x)\)，我们设想用一个联合概率分布 \(q(x,z)\) 来逼近 \(p(x,z)\)，那么我们用KL散度来看它们的距离：

\[KL\Big(p(x,z)\Big\Vert q(x,z)\Big) = \iint p(x,z)\ln \frac{p(x,z)}{q(x,z)} dzdx\tag{16}\]

KL散度是我们的终极目标，因为我们希望两个分布越接近越好，所以KL散度越小越好。当然，由于现在 \(p(x,z)\) 也有参数，所以不单单是 \(q(x,z)\) 来逼近 \(p(x,z)\)，\(p(x,z)\)也会主动来逼近\(q(x,z)\)，两者是相互接近。

于是我们有

\[\begin{aligned}KL\Big(p(x,z)\Big\Vert q(x,z)\Big) =& \int \tilde{p}(x) \left[\int p(z|x)\ln \frac{\tilde{p}(x)p(z|x)}{q(x,z)} dz\right]dx\\ =& \mathbb{E}_{x\sim \tilde{p}(x)} \left[\int p(z|x)\ln \frac{\tilde{p}(x)p(z|x)}{q(x,z)} dz\right] \end{aligned}\tag{17}\]

这样一来利用 (12)，把各个 \(x_i\) 代入就可以进行计算了，这个式子还可以进一步简化，因为\(\ln \frac{\tilde{p}(x)p(z|x)}{q(x,z)}=\ln \tilde{p}(x) + \ln \frac{p(z|x)}{q(x,z)}\)，而

\[\begin{aligned}\mathbb{E}{x\sim \tilde{p}(x)} \left[\int p(z|x)\ln \tilde{p}(x)dz\right] =& \mathbb{E}{x\sim \tilde{p}(x)} \left[\ln \tilde{p}(x)\int p(z|x)dz\right]\\ =&\mathbb{E}_{x\sim \tilde{p}(x)} \big[\ln \tilde{p}(x)\big] \end{aligned}\tag{18}\]

注意这里的 \(\tilde{p}(x)\) 是根据样本 \(x_1,x_2,\dots,x_n\) 确定的关于 \(x\) 的先验分布，尽管我们不一定能准确写出它的形式，但它是确定的、存在的，因此这一项只是一个常数，所以可以写出

\[\mathcal{L}=KL\Big(p(x,z)\Big\Vert q(x,z)\Big) - \text{常数}= \mathbb{E}_{x\sim \tilde{p}(x)} \left[\int p(z|x)\ln \frac{p(z|x)}{q(x,z)} dz\right]\tag{19}\]

目前最小化 \(KL\Big(p(x,z)\Big\Vert q(x,z)\Big)\) 也就等价于最小化 \(\mathcal{L}\)。注意减去的常数为\(\mathbb{E}{x\sim \tilde{p}(x)} \big[\ln \tilde{p}(x)\big]\)，所以\(\mathcal{L}\)拥有下界 \(-\mathbb{E}{x\sim \tilde{p}(x)} \big[\ln \tilde{p}(x)\big]\) 注意到\(\tilde{p}(x)\)不一定是概率，在连续情形时 \(\tilde{p}(x)\) 是概率密度，它可以大于1也可以小于1，所以 \(-\mathbb{E}_{x\sim \tilde{p}(x)} \big[\ln \tilde{p}(x)\big]\) 不一定是非负，即loss可能是负数。

你的VAE已经送达

到这里，我们回顾初衷——为了得到生成模型，所以我们把 \(q(x,z)\) 写成 \(q(x|z)q(z)\)，于是就有

\[\begin{aligned}\mathcal{L} =& \mathbb{E}{x\sim \tilde{p}(x)} \left[\int p(z|x)\ln \frac{p(z|x)}{q(x|z)q(z)} dz\right]\\ =&\mathbb{E}{x\sim \tilde{p}(x)} \left[-\int p(z|x)\ln q(x|z)dz+\int p(z|x)\ln \frac{p(z|x)}{q(z)}dz\right]\end{aligned}\tag{20}\]

再简明一点，那就是

\[\begin{aligned}\mathcal{L} = &\mathbb{E}{x\sim \tilde{p}(x)} \left[\mathbb{E}{z\sim p(z|x)}\big[-\ln q(x|z)\big]+\mathbb{E}{z\sim p(z|x)}\Big[\ln \frac{p(z|x)}{q(z)}\Big]\right]\\ = &\mathbb{E}{x\sim \tilde{p}(x)} \Bigg[\mathbb{E}_{z\sim p(z|x)}\big[-\ln q(x|z)\big]+KL\Big(p(z|x)\Big\Vert q(z)\Big)\Bigg] \end{aligned}\tag{21}\]

看，括号内的不就是VAE的损失函数嘛？只不过我们换了个符号而已。我们就是要想办法找到适当的\(q(x|z)\) 和 \(q(z)\) 使得 \(\mathcal{L}\) 最小化。

再回顾一下整个过程，我们几乎都没做什么“让人难以想到”的形式变换，但VAE就出来了。所以，没有必要去对后验分布进行分析，直面联合分布，我们能更快捷地到达终点。

不能搞分裂

鉴于(21)式的特点，我们也许会将 \(\mathcal{L}\) 分开为两部分看：\(\mathbb{E}_{z\sim p(z|x)}\big[-\ln q(x|z)\big]\) 的期望和\(KL\Big(p(z|x)\Big\Vert q(z)\Big)\) 的期望，并且认为问题变成了两个loss的分别最小化。

然而这种看法是不妥的，因为\(KL\Big(p(z|x)\Big\Vert q(z)\Big)=0\) 意味着 \(z\) 没有任何辨识度，所以 \(-\ln q(x|z)\) 不可能小（预测不准），而如果 \(-\ln q(x|z)\) 小则 \(q(x|z)\) 大，预测准确，这时候 \(p(z|x)\) 不会太随机，即 \(KL\Big(p(z|x)\Big\Vert q(z)\Big)\) 不会小，所以这两部分的loss其实是相互拮抗的。所以，\(\mathcal{L}\) 不能割裂来看，而是要整体来看，整个的 \(\mathcal{L}\) 越小模型就越接近收敛，而不能只单独观察某一部分的loss。

事实上，这正是GAN模型中梦寐以求的——有一个总指标能够指示生成模型的训练进程，在VAE模型中天然就具备了这种能力了，而GAN中要到WGAN才有这么一个指标～

实验

截止上面的内容，其实我们已经完成了VAE整体的理论构建。但为了要将它付诸于实验，还需要做一些工作。事实上原论文《Auto-Encoding Variational Bayes》也在这部分做了比较充分的展开，但遗憾的是，网上很多VAE教程都只是推导到(13)式就没有细说了。

后验分布近似

现在 \(q(z),q(x|z),p(z|x)\) 全都是未知的，连形式都还没确定，而为了实验，就得把 (21) 的每一项都明确写出来。

首先，为了便于采样，我们假设 \(z\sim N(0,I)\)，即标准的多元正态分布，这就解决了 \(q(z)\)。那\(q(x|z),p(z|x)\) 呢？一股脑用神经网络拟合吧。

💡注：本来如果已知 \(q(x|z)\) 和\( q(z)\)，那么\( p(z|x) \)最合理的估计应该是：
\[\hat{p}(z|x) = q(z|x) = \frac{q(x|z)q(z)}{q(x)} = \frac{q(x|z)q(z)}{\int q(x|z)q(z)dz}\tag{22}\]
这其实就是EM算法中的后验概率估计的步骤，具体可以参考《从最大似然到EM算法：一致的理解方式》。但事实上，分母的积分几乎不可能完成，因此这是行不通的。所以干脆用一般的网络去近似它，这样不一定能达到最优，但终究是一个可用的近似。

具体来说，我们假设 \(p(z|x)\) 也是（各分量独立的）正态分布，其均值和方差由 \(x\) 来决定，这个“决定”，就是一个神经网络：

\[p(z|x)=\frac{1}{\prod\limits_{k=1}^d \sqrt{2\pi \sigma_{(k)}^2(x)}}\exp\left(-\frac{1}{2}\left\Vert\frac{z-\mu(x)}{\sigma(x)}\right\Vert^2\right)\tag{23}\]

这里的\(\mu(x),\sigma^2(x)\) 是输入为 \(x\)、输出分别为均值和方差的神经网络，其中 \(\mu(x)\) 就起到了类似encoder的作用。既然假定了高斯分布，那么(21)式中的KL散度这一项就可以先算出来：

\[KL\Big(p(z|x)\Big\Vert q(z)\Big)=\frac{1}{2} \sum_{k=1}^d \Big(\mu_{(k)}^2(x) + \sigma_{(k)}^2(x) - \ln \sigma_{(k)}^2(x) - 1\Big)\tag{24}\]

也就是我们所说的KL loss，这在上面已经给出。

生成模型近似

现在只剩生成模型部分 \(q(x|z)\) 了，该选什么分布呢？论文《Auto-Encoding Variational Bayes》给出了两种候选方案：伯努利分布或正态分布。

什么？又是正态分布？是不是太过简化了？然而并没有办法，因为我们要构造一个分布，而不是任意一个函数，既然是分布就得满足归一化的要求，而要满足归一化，又要容易算，我们还真没多少选择。

伯努利分布模型

首先来看伯努利分布，众所周知它其实就是一个二元分布：

\[p(\xi)=\left\{\begin{aligned}&\rho,\, \xi = 1;\\ &1-\rho,\, \xi = 0\end{aligned}\right.\tag{25}\]

所以伯努利分布只适用于 \(x\) 是一个多元的二值向量的情况，比如 \(x\) 是二值图像时（mnist可以看成是这种情况）。这种情况下，我们用神经网络 \(\rho(z)\) 来算参数\(\rho\)，从而得到

\[q(x|z)=\prod_{k=1}^D \Big(\rho_{(k)}(z)\Big)^{x_{(k)}} \Big(1 - \rho_{(k)}(z)\Big)^{1 - x_{(k)}}\tag{26}\]

这时候可以算出

\[-\ln q(x|z) = \sum_{k=1}^D \Big[- x_{(k)} \ln \rho_{(k)}(z) - (1-x_{(k)}) \ln \Big(1 -\rho_{(k)}(z)\Big)\Big]\tag{27}\]

这表明 \(\rho(z)\) 要压缩到0～1之间（比如用sigmoid激活），然后用交叉熵作为损失函数，这里\(\rho(z)\)就起到了类似decoder的作用。

正态分布模型

然后是正态分布，这跟\(p(z|x)\) 是一样的，只不过\(x,z\)交换了位置：

\[q(x|z)=\frac{1}{\prod\limits_{k=1}^D \sqrt{2\pi \tilde{\sigma}_{(k)}^2(z)}}\exp\left(-\frac{1}{2}\left\Vert\frac{x-\tilde{\mu}(z)}{\tilde{\sigma}(z)}\right\Vert^2\right)\tag{28}\]

这里的 \(\tilde{\mu}(z),\tilde{\sigma}^2(z)\) 是输入为\(z\)、输出分别为均值和方差的神经网络，\(\tilde{\mu}(z)\)就起到了decoder的作用。于是

\[-\ln q(x|z) = \frac{1}{2}\left\Vert\frac{x-\tilde{\mu}(z)}{\tilde{\sigma}(z)}\right\Vert^2 + \frac{D}{2}\ln 2\pi + \frac{1}{2}\sum_{k=1}^D \ln \tilde{\sigma}_{(k)}^2(z)\tag{29}\]

很多时候我们会固定方差为一个常数 \(\tilde{\sigma}^2\)，这时候

\[-\ln q(x|z) \sim \frac{1}{2\tilde{\sigma}^2}\Big\Vert x-\tilde{\mu}(z)\Big\Vert^2\tag{30}\]

这就出现了MSE损失函数。

所以现在就清楚了，对于二值数据，我们可以对decoder用sigmoid函数激活，然后用交叉熵作为损失函数，这对应于\(q(x|z)\)为伯努利分布；而对于一般数据，我们用MSE作为损失函数，这对应于\(q(x|z)\)为固定方差的正态分布。

采样计算技巧

前一节做了那么多的事情，无非是希望能(21)明确地写下来。当我们假设 \(p(z|x)\) 和 \(q(z)\) 都是正态分布时， (21) 的KL散度部分就已经算出来了，结果是(24)式；当我们假设 \(q(x|z)\) 是伯努利分布或者高斯分布时，\(-\ln q(x|z)\) 也能算出来了。现在缺什么呢？

采样！

\(p(z|x)\)的作用分两部分，一部分是用来算 \(KL\Big(p(z|x)\Big\Vert q(z)\Big)\)，另一部分是用来算 \(\mathbb{E}{z\sim p(z|x)}\big[-\ln q(x|z)\big]\) 的，而\(\mathbb{E}{z\sim p(z|x)}\big[-\ln q(x|z)\big]\)就意味着

\[-\frac{1}{n}\sum_{i=1}^n \ln q(x|z_i),\quad z_i \sim p(z|x)\tag{31}\]

我们已经假定了 \(p(z|x)\) 是正态分布，均值和方差由模型来算，这样一来，借助“重参数技巧”就可以完成采样。

但是采样多少个才适合呢？VAE非常直接了当：一个！所以这时候(21)就变得非常简单了：

\[\mathcal{L} = \mathbb{E}_{x\sim \tilde{p}(x)} \Bigg[-\ln q(x|z) + KL\Big(p(z|x)\Big\Vert q(z)\Big)\Bigg],\quad z\sim p(z|x)\tag{32}\]

该式中的每一项，可以在把(24),(27),(29),(30)式找到。注意对于一个batch中的每个 \(x\)，都需要从\(p(z|x)\) 采样一个“专属”于\(x\)的 \(z\) 出来才去算 \(-\ln q(x|z)\)。而正因为VAE在 \(p(z|x)\) 这里只采样了一个样本，所以它看起来就跟普通的AE差不多了。

那么最后的问题就是采样一个究竟够了吗？事实上我们会运行多个epoch，每次的隐变量都是随机生成的，因此当epoch数足够多时，事实上是可以保证采样的充分性的。我也实验过采样多个的情形，感觉生成的样本并没有明显变化。

Reference

变分自编码器（一）：原来是这么一回事 - 科学空间|Scientific Spaces

变分自编码器（二）：从贝叶斯观点出发 - 科学空间|Scientific Spaces

#

!

VAE 变分自编码器