研究对象与基本设定
我们希望学习一个能够“生成数据”的概率模型。假设我们有一个数据集 \(D\),每个样本是 \(n\) 维二值向量:\(x \in \{0,1\}^n\)
我们的目标是用一个参数化分布 \(p_\theta(x)\) 去逼近真实数据分布 \(p_{\text{data}}(x)\),并最终能够:
- 密度估计:给定 \(x\) 计算 \(p_\theta(x)\) 或 \(\log p_\theta(x)\)
- 采样生成:从 \(p_\theta(x)\) 采样得到新的 \(x\)
表示:链式法则与自回归分解
链式法则分解联合分布
任意联合分布都可用概率链式法则分解为条件概率的乘积:
其中:\(x_{<i} = [x_1, x_2, \dots, x_{i-1}]\),这意味着:只要我们能为每个维度 \(i\) 学好一个条件分布 \(p(x_i \mid x_{<i})\),就能得到完整的 \(p(x)\)。
自回归(Autoregressive)性质
- 模型固定一个变量顺序 \(x_1, x_2, \dots, x_n\)
- 每个 \(x_i\) 的分布依赖于所有“之前”的变量 \(x_{<i}\)
- 不做额外条件独立假设(即“全连接依赖”)
这一结构也可理解为一个贝叶斯网络:每个节点 \(x_i\) 指向未来所有节点,或至少依赖所有过去节点。可以图形化地表示为贝叶斯网络
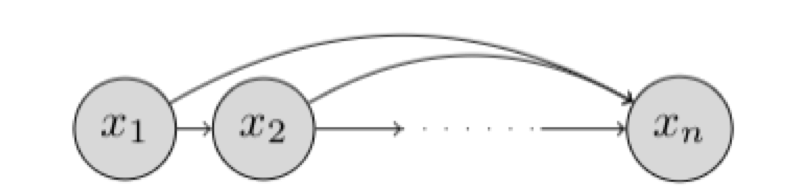
为什么不能直接用表格表示条件分布?
假设我们想用“查表”的方式表示条件分布,例如最后一维:\(p(x_n \mid x_{<n})\)
由于 \(x_{<n} \in \{0,1\}^{n-1}\),共有 \(2^{n-1}\) 种配置。对每种配置你需要指定 \(p(x_n=1\mid x_{<n})\)(因为二值变量另一项由归一化确定)。
因此参数量大致为:\(2^{n-1} - 1\),这会随 \(n\) 指数爆炸,完全不可用。
自回归生成模型:用参数化函数表示条件分布
核心思想:不查表,而是用一个带固定参数量的函数去预测条件分布参数。
因为 \(x_i\) 是二值变量,最自然是用伯努利分布:
其中:
- \(f_i:\{0,1\}^{i-1}\to [0,1]\) 输出伯努利均值(即 \(p(x_i=1\mid x_{<i})\))
- \(\theta_i\) 是第 \(i\) 个条件分布对应的参数
- 总参数量为 \(\sum_{i=1}^{n} |\theta_i|\),通常远小于指数级
代价是:与表格设置不同,自回归生成模型不能表示所有可能的分布。其表达能力受限于我们限制条件分布对应于均值为通过受限类参数化函数指定的伯努利随机变量的事实, 即,模型表达能力受限于你选择的函数族 \(f_i(\cdot)\)。
FVSBN(Fully-Visible Sigmoid Belief Network)
最简单的 \(f_i\):线性 + sigmoid:
其中:
- \(\sigma(\cdot)\) 为 sigmoid 函数,把实数映射到 \([0,1]\)
- \(\theta_i = \{\alpha_0^{(i)},\alpha_1^{(i)},\dots,\alpha_{i-1}^{(i)}\}\), 表示均值函数的参数
第 \(i\) 个条件分布需要 \(i\) 个参数,因此总参数量:\(\sum_{i=1}^{n} i = \mathcal{O}(n^2)\)。相比查表的指数复杂度已经大幅下降,但表达能力也较有限(本质是逐维 logistic 回归)。
用 MLP 增强表达力
用一个一层隐藏层的网络定义 \(f_i\):变量 \(i\) 的均值函数可以表示为
参数包括:\(\theta_i = \{A_i \in \mathbb{R}^{d\times (i-1)},\ c_i\in \mathbb{R}^d,\ \alpha^{(i)}\in \mathbb{R}^d,\ b_i\in \mathbb{R}\}\). 参数量主要由 \(A_i\) 决定,总体约为:\(\mathcal{O}(n^2 d)\)
问题:对每个 \(i\) 都有单独的网络(尤其是 \(A_i\) 尺寸不断增长),既费参数也费计算。
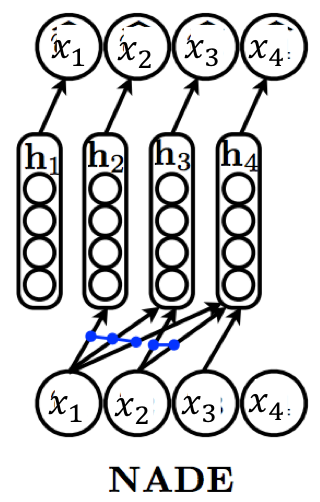
NADE:Neural Autoregressive Density Estimator
NADE 的核心是让不同维度的条件分布共享一套“输入到隐层”的权重。
NADE 定义:
其中:
- \(W \in \mathbb{R}^{d \times n}\) 为共享矩阵
- \(W_{\cdot,<i}\) 表示取前 \(i-1\) 列(对应 \(x_{<i}\))
- \(c \in \mathbb{R}^d\) 为共享偏置
整体参数集合:\(\theta = \{W\in \mathbb{R}^{d\times n},\ c\in \mathbb{R}^d,\ \{\alpha^{(i)}\}_{i=1}^n,\ \{b_i\}_{i=1}^n\}\)
共享参数提供了两大收益
- 参数量显著降低:从朴素 MLP 的 \(\mathcal{O}(n^2 d)\) 降到:\(\mathcal{O}(nd)\)
- 计算可递推,整体 \(\mathcal{O}(nd)\) :NADE 可用递推方式更新隐藏层的“预激活”,避免每次从头计算(原文提到 base case 为 \(a_1=c\),后续可逐步加入第 \(i-1\) 个输入贡献)。直观上:
- 从 \(i\) 到 \(i+1\) 只多了一项与 \(x_i\) 相关的增量
- 因此可做到线性时间遍历所有条件
从 KL 到最大似然(MLE)
生成模型涉及优化数据和模型分布之间的接近程度。常用的接近程度概念是数据与模型分布之间的 KL 散度:
两点重要提醒:
- KL 不对称: \( D_{\text{KL}}(p,q) \neq D_{\text{KL}}(q,p)\) ,优化反向 KL 可能带来不同的行为。、
- 强烈惩罚漏覆盖(zero-prob): 若存在 \(x\sim p_{\text{data}}\) 但 \(p_\theta(x)=0\),则目标变为 \(+\infty\)。
因为 \(p_{\text{data}}\) 不依赖 \(\theta\),上述最小化等价于最大化:
数据集 \(D\) 视为 i.i.d. 采样,可用 Monte Carlo 估计:
在实践中,我们使用小批量梯度上升来优化 MLE 目标。该算法以迭代方式运行。每次迭代 \(t\) 取一个 mini-batch \(B_t\),更新:
其中 \(r_t\) 为学习率(可调度)。实践中常用 Adam、RMSProp 等变体。
现在我们已经有了明确的优化目标和优化过程,剩下的唯一任务就是在自回归生成模型的上下文中评估目标。为此,我们把自回归分解代入似然:
因此训练目标变为:
这点非常重要:训练时每个样本的 log-likelihood 可以拆成逐维的条件对数概率之和,实现和优化都很直接。
模型生成和推理
在自回归模型中的推理非常直接。对于任意点 \(x\) 的密度估计,我们只需评估每个 \(i\) 的 log-conditionals \(p(x_i\mid x_{<i})\) ,并将这些值相加,以获得模型分配给 \(x\) 的对数似然。由于我们知道条件向量 \(x\) ,每个条件都可以并行评估。因此,在现代硬件上密度估计是高效的。
但是对于自回归模型的采样生成是串行的
采样必须按顺序进行:
- 先采 \(x_1 \sim p(x_1)\)
- 再采 \(x_2 \sim p(x_2\mid x_1)\)
- …
- 最后采 \(x_n \sim p(x_n\mid x_{<n})\)
因此生成复杂高维数据(如音频)时会很慢。