题意
给定平面上一个圆的圆心位置和半径,从圆中以均匀的概率随机选取点。
分析
拒绝取样
其实我的第一反应是用拒绝取样(Rejection Sampling)的思路来做:首先从这个圆的与坐标轴平行的外切正方形中均匀随机选取点,然后判断点是否位于圆中;如果不在,重新生成一个新的点,再次进行判断;否则直接返回。
直觉上来说,拒绝取样显然是正确的;不过我们可以用一种稍微更加形式化的方法来描述。(以下内容参考了拒绝采样(reject sampling)的简单认识,非常直观形象。)
下图是一个随机变量的密度函数曲线,试问如何获得这个随机变量的样本呢?
如果你像我一样,已经把概率论与数理统计统统还给数学老师了,那么提示一下,概率密度函数(PDF)是累积分布函数(CDF)的导数,反映的是概率的“密集程度”。你可以设想一根极细的无穷长的金属杆,概率密度相当于杆上各点的质量密度。由于上述原因,概率密度函数曲线下的面积表示的就是取值概率。(参考了应该如何理解概率分布函数和概率密度函数?)
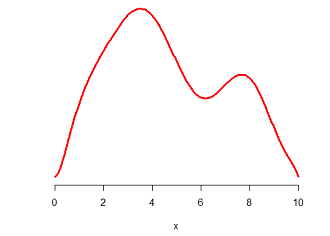
我们首先用一个矩形将这个密度曲线套起来,把密度曲线框在一个矩形里,如下图所示:

然后,向这个矩形里随机投点。随机投点意味着在矩形这块区域内,这些点是满足均匀分布的。投了大概10000个点,如下面这个样子:
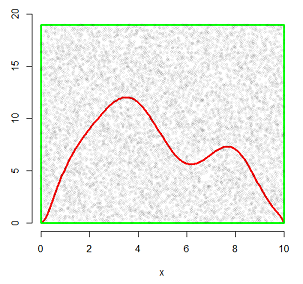
显然,有的点落在了密度曲线下侧,有的点落在了密度曲线的上侧。上侧的点用绿色来表示,下侧的点用蓝色来表示,如下图:

只保留密度曲线下侧的点,即蓝色的点:

到这里,提一个问题:在密度曲线以下的这块区域里,这些点满足什么分布?均匀分布!这是拒绝采样最关键的部分,搞个矩形、向矩形里投点等等,所做的一切都是为了获得一个密度曲线所围成区域的均匀分布。只要能获得这样一个在密度曲线下满足均匀分布的样本,我们就可以获得与该密度曲线相匹配的随机变量的采样样本。方法是,只需把每个蓝点的横坐标提取出来,这些横坐标所构成的样本就是我们的目标样本。下图左侧,是按照以上方法获得的一个样本的直方图以及核密度估计,下图右侧,是开始的密度曲线。

极坐标法
先用角度随机选择一条半径,然后在这条半径上随机选择一个点。但问题是我们不能把圆这样看成是很多半径的集合——或者说,这条半径上不同位置的点的密集程度是不一样的。显然距离圆心更远的一端被选择的概率应该更大。
直接对角度和半径都进行随机取样会产生这样的后果,靠近圆心的点被选择的概率偏大(Uniform random points in a circle using polar coordinates):

我们重新考虑一下半径的问题。以半径\(r\)作为随机变量,则随机点落在\(r\)范围内的概率分布为
以[0, 1]均匀分布对\(CDF(r)\)进行随机,则有\(r=R\sqrt{rand()}\)。
class Solution:
def __init__(self, radius: float, x_center: float, y_center: float):
self.radius = radius
self.x_center = x_center
self.y_center = y_center
def randPoint(self) -> List[float]:
theta = random.uniform(0, 1) * 2 * math.pi
p = math.sqrt(random.uniform(0, 1)) * self.radius
return [self.x_center + p * math.sin(theta), self.y_center + p * math.cos(theta)]