CTR预测问题简介

点击率(Click Through Rate, CTR)预估是程序化广告里的一个最基本而又最重要的问题。比如在竞价广告里，排序的依据就是$𝑐𝑡𝑟×𝑏𝑖𝑑$。通过选择$𝑐𝑡𝑟×𝑏𝑖𝑑$最大的广告就能最大化平台的eCPM。从机器学习的角度来说这是一个普通的回归问题，但是它的特殊性在于训练数据只有0/1的值——因为我们没有办法给同一个用户展示同一个广告1万次，然后统计点击的次数来估计真实的点击率。另外有人也许会有这样的看法：对于某一个特定的曝光，某个用户是否点击某个广告是确定的，第一次不点，第二次也不会点，因此点击率是一个0/1的固定值而不是一个0-1之间的概率值。这个说法有一些道理，原因是第二次实验和第一次使用不是独立同分布的。“真正”的做法是第二次做实验前要擦除用户第一次实验的记忆，然后在一模一样的场景(时间、地点……)下做N次独立实验。但是我们也可能从另外一个角度理解点击率：有很多用户比较类似，比如类似的用户有1万个，在相同的条件下他们点击的次数和除以1万可以看成点击率。如果从“上帝”视角来看，如果能预知未来，那么确实可以知道每一个用户是否会点击某个广告，然后能够准确的估计这一次是否会点击。但是实际由于我们信息的缺失和计算能力的限制，我们不可能准确的提前预估。如果在训练数据上精确的预估了0/1这样的点击率，那么更可能是过拟合了。

另外有一点就是我们采集的数据是有偏的。比如在CPC的竞价广告中，我们收集到的都是竞价获胜的广告，而竞价又是受CTR的影响，因此会产生放大作用——CTR估计的越低，则竞价获胜的可能性越低，曝光的次数也越少，从而点击率估计的也有偏。

评价指标

评价CTR的最常见指标是$logloss$和AUC。$logloss$就是计算真实分布和预测分布的交叉熵，计算公式为：
在AUC之前，要简单介绍一下混淆矩阵

数据特点

CTR数据的特征一般可以分为三大类：用户的特征、广告的特征和上下文特征。对于搜索来说，主要的特征包含用户特征、query特征、商品特征。用户的特征包括用户性别、年龄、职业、教育水平等等；创意的特征包括广告的行业(旅游、电商，……)、标签等等；上下文的特征包括广告的位置、用户使用的设备、浏览器、时间、地点等。这些特征有一部分是连续的值，比如年龄；而更多的特征是Category(类别)的特征，比如性别为两类的男女，职业可以是销售、产品经理、……。对于Category的特征，我们通常使用one-hot的编码把它变成一个高纬的稀疏向量，比如职业细分的话可能几十上百种，地域按照城市分可能成千上万。另外为了提高模型的泛化能力我们可能把连续的特征进行离散化（分桶），比如把年龄分为18岁以下、18-29、30-40，……。这样的每一个输入特征向量可能是非常高维的一个稀疏的向量

FM（Factorization Machine）

在FM模型之前，CTR预估最常用的模型是SVM和LR(包括用GBDT给它们提取非线性特征)。SVM和LR都是线性的模型(SVM理论上可以引入核函数从而引入非线性，但是由于非常高维的稀疏特征向量使得它很容易过拟合，因此实际很少用)，但是实际的这些特征是有相关性的。比如根据论文DeepFM: A Factorization-Machine based Neural Network for CTR Prediction的调研，在主流的app应用市场里，在吃饭的时间点食谱类app的下载量明显会比平时更大，因此app的类别和时间会存在二阶的关系。另外一个例子是年轻男性更喜欢射击类游戏，这是年龄、性别和游戏类别的三阶关系。因此怎么建模二阶、三阶甚至更高阶的非线性的关系是预估能够更加准确的关键点。

我们可以直接建模二阶关系：

\[ y(x)=w_0+\sum_{i=1}^{n}w_ix_i+\sum_{i=1}^{n}\sum_{j=i+1}^{n}w_{ij}x_ix_j\tag{1} \]

其中，$n$是特征向量的维度，$𝑥_𝑖$是第$i$维特征，$𝑤_0、𝑤_𝑖、𝑤_{𝑖𝑗}$是模型参数。这种方法的问题是二阶关系的参数个数是$𝑛(𝑛−1)/2$，这样会导致模型的参数很多，另外因为特征向量非常稀疏，二次项参数的训练是很困难的。其原因是，每个参数 $𝑤_{𝑖𝑗}$的训练需要大量$𝑥_𝑖$和$𝑥_𝑗$都非零的样本；由于样本数据本来就比较稀疏，满足“$𝑥_𝑖$和$𝑥_𝑗$都非零”的样本将会非常少。训练样本的不足，很容易导致参数 $𝑤_{𝑖𝑗}$不准确，最终将严重影响模型的性能。

那么，如何解决二次项参数的训练问题呢？矩阵分解提供了一种解决思路。根据Factorization Machines中在model-based的协同过滤，一个rating矩阵可以分解为user矩阵和item矩阵，每个user和item都可以采用一个隐向量表示。比如在下图中的例子中，我们把每个user表示成一个二维向量，同时把每个item表示成一个二维向量，两个向量的点积就是矩阵中user对item的打分

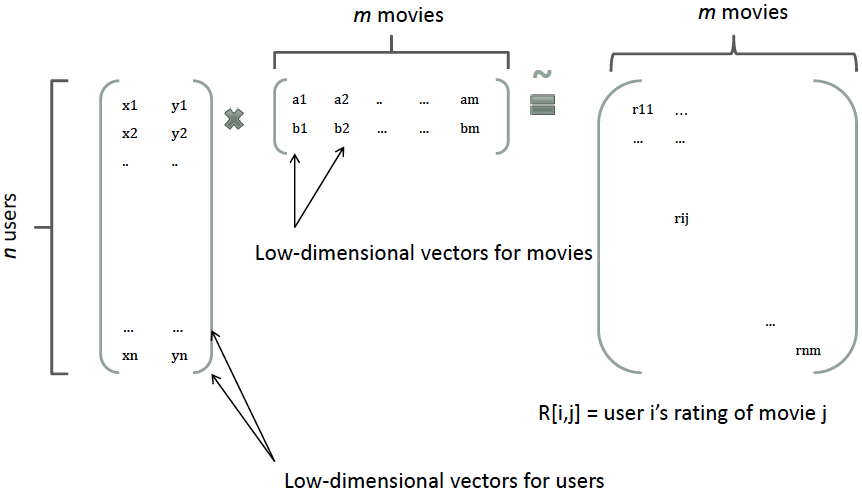
类似地，所有二次项参数 $𝑤_{𝑖𝑗}$可以组成一个对称阵$𝐖$（为了方便说明FM的由来，对角元素可以设置为正实数），那么这个矩阵就可以分解为$ 𝐖=𝐕^𝑇𝐕$，$𝐕$ 的第$j$列便是第$j$维特征的隐向量。换句话说，每个参数 $𝑤_{𝑖𝑗}=⟨𝐯_𝑖,𝐯_𝑗⟩$，这就是FM模型的核心思想。因此，FM的模型方程为（本文不讨论FM的高阶形式）

\[ y(x)=w_0+\sum_{i=1}^{n}w_ix_i+\sum_{i=1}^{n}\sum_{j=i+1}^{n}\langle\mathbf{v_i},\mathbf{v_j}\rangle x_ix_j \tag{2} \]

其中，$𝑣_𝑖$ 是第$ i $维特征的隐向量，$⟨⋅,⋅⟩ $代表向量点积。隐向量的长度为$ 𝑘(𝑘«𝑛)$，包含 \(k$ 个描述特征的因子。根据公式(2)，二次项的参数数量减少为 $𝑘𝑛$个，远少于多项式模型的参数数量。另外，参数因子化使得 $𝑥_ℎ𝑥_𝑖$ 的参数和 (𝑥_𝑖𝑥_𝑗 $的参数不再是相互独立的，因此我们可以在样本稀疏的情况下相对合理地估计FM的二次项参数。具体来说，$𝑥_ℎ𝑥_𝑖 $和$ 𝑥_𝑖𝑥_𝑗\) 的系数分别为\) \langle\mathbf{v_h},\mathbf{v_i}\rangle$和 $ \langle\mathbf{v_i},\mathbf{v_j}\rangle$，它们之间有共同项 \(\mathbf{v_i}$。也就是说，所有包含“\)𝑥_𝑖 $的非零组合特征”（存在某个 \(𝑗≠𝑖$，使得 $𝑥_𝑖𝑥_𝑗≠0$）的样本都可以用来学习隐向量 $𝐯_𝑖$，这很大程度上避免了数据稀疏性造成的影响。而在多项式模型中，\)𝑤_{ℎ𝑖}$和 $w_{ij}$ 是相互独立的。

直观上看，FM的复杂度是 $𝑂(𝑘𝑛^2)$。但是，通过下式，FM的二次项可以化简，其复杂度可以优化到 $𝑂(𝑘𝑛)$。由此可见，FM可以在线性时间对新样本作出预测。

\[ \sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j = \frac{1}{2} \sum_{f=1}^k \left(\left( \sum_{i=1}^n v_{i, f} x_i \right)^2 - \sum_{i=1}^n v_{i, f}^2 x_i^2 \right) \]

下面是上式的推导过程:

\[ \begin{aligned}&\sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j \\ &= \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j - \frac{1}{2} \sum_{i=1}^n \langle \mathbf{v}_i, \mathbf{v}_i \rangle x_i x_i \\ &= \frac{1}{2} \left( \sum_{i=1}^n \sum_{j=1}^n \sum_{f=1}^k v_{if}v_{jf} x_i x_j - \sum_{i=1}^n \sum_{f=1}^k v_{if}v_{if} x_i x_i \right) \\ &= \frac{1}{2} \sum_{f=1}^k \left( \left(\sum_{i=1}^n v_{if}x_i \right) \left( \sum_{j=1}^n v_{jf}x_j \right) -\sum_{i=1}^n v_{i,f}^2x_i^2 \right) \\ &= \frac{1}{2} \sum_{f=1}^k \left( \left(\sum_{i=1}^n v_{if}x_i \right)^2 -\sum_{i=1}^n v_{i,f}^2x_i^2\right)\end{aligned} \]

训练的时候可以使用随机梯度下降算法，梯度计算公式为：

\[ \frac{\partial}{\partial\theta} \hat{y} (\mathbf{x}) = \begin{cases} 1, & \text{if }\theta \text{ is }w_0 \\ x_i, & \text{if } \theta \text{ is } x_i \\ x_i \sum_{j=1}^nv_{j,f}x_j-v_{i,f}x_i^2 , & \text{if } \theta \text{ is } v_{i,f} \end{cases} \]

其中，$𝑣_{𝑗,𝑓}$是隐向量 $𝐯_𝑗 $的第 \(𝑓$ 个元素。由于 (\sum_{𝑗=1}^n𝑣_{𝑗,𝑓}𝑥_𝑗 (只与 (f $有关，而与$ i $无关，在每次迭代过程中，只需计算一次所有$ f (的 $\sum_{𝑗=1}^n𝑣_{𝑗,𝑓}𝑥_𝑗$，就能够方便地得到所有 𝑣𝑖,𝑓 的梯度。显然，计算所有 (f $的$\sum_{𝑗=1}n𝑣_{𝑗,𝑓}𝑥_𝑗\)的复杂度是\) 𝑂(𝑘𝑛)\)；已知\)\sum_{𝑗=1}n𝑣_{𝑗,𝑓}𝑥_𝑗\)时，计算每个参数梯度的复杂度是 $𝑂(1)$；得到梯度后，更新每个参数的复杂度是 $𝑂(1)$；模型参数一共有\) 𝑛𝑘+𝑛+1 $个。因此，FM参数训练的复杂度也是 $𝑂(𝑘𝑛)$。

DeepFM

概述

像LR/SVM这样的模型无法建模非线性的特征交互(interaction)，我们只能人工组特征的交叉或者组合，比如通过数据分析发现时间和食谱类的app存在比较强的关联关系，然后把这个特征加到线性模型里去。这种方法的确定是需要人工做特征工程，成本很高，而且很多复杂的特征交互很难发现，就像啤酒和纸尿布这样的关系，我们只能做事后诸葛亮这样的分析：啊哈，确实很有道理，但是不做大量的数据分析想提前发现就比较困难。

FM通过给每个特征引入一个低维稠密的隐向量来减少二阶特征交互的参数个数，同时实现信息共享，使得在非常稀疏的特征向量上的学习更加容易泛化。理论上FM可以建模二阶以上的特征交互，但是由于计算量急剧增加，实际一般只用二阶的模型。

而(深度)神经网络的优势就是可以多层的网络结构更好的进行特征表示，从而学习高阶的非线性关系。DeepFM的思想就是结合FM在一阶和二阶特征的简洁高效和深度学习在高阶特征交互上的优势，同时通过共享FM和DNN的Embedding来减少参数量和共享信息，从而得到更好的模型。

方法简介

假设训练数据的个数为$n$，每一个训练样本为$(\mathcal{X},y)$，其中$\mathcal{X}$由m个field组成，而$𝑦∈0,1$表示用户是否点击。($\mathcal{X}$的field可以是category的field，比如性别和地域等；也可以是连续的field，比如年龄。总的field个数可能只有几百个，但是如果用one-hot编码展开的话，这个特征向量会非常高维并且稀疏。我们把每一个$𝑥_𝑖$记为$𝑥_𝑖=[𝑥_{𝑓𝑖𝑒𝑙𝑑1},𝑥_{𝑓𝑖𝑒𝑙𝑑2},…,𝑥_{𝑓𝑖𝑒𝑙𝑑𝑚}]$，其中每一个$𝑥_{𝑓𝑖𝑒𝑙𝑑_𝑖}$是其向量表示(连续的field就是1维的，而Category的field则用one-hot展开)。

DeepFM包括FM和DNN两个部分，最终的预测由两部分输出的相加得到：

\[ \hat{y}=sigmoid(y_{FM}+y_{DNN}) \]

其中$𝑦_{𝐹𝑀}$是FM模型的输出，而$𝑦_{𝐷𝑁𝑁}$是DNN的输出。模型的结构如下图所示，它包含FM和DNN两个组件。

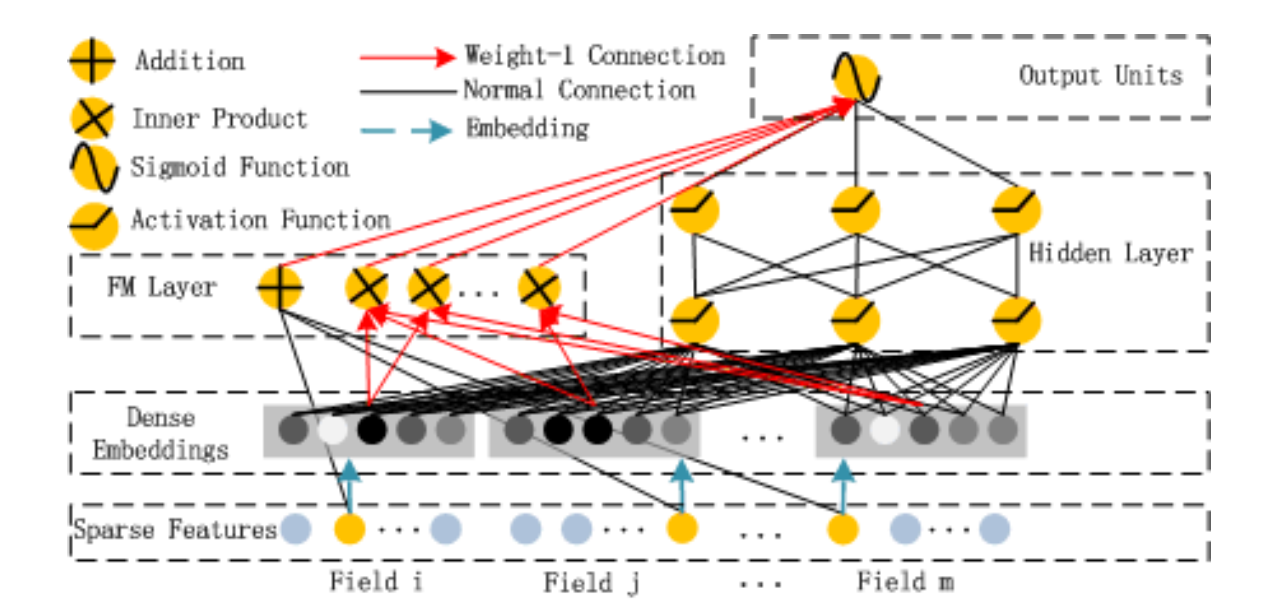
下面我们分别来看这两个组件。

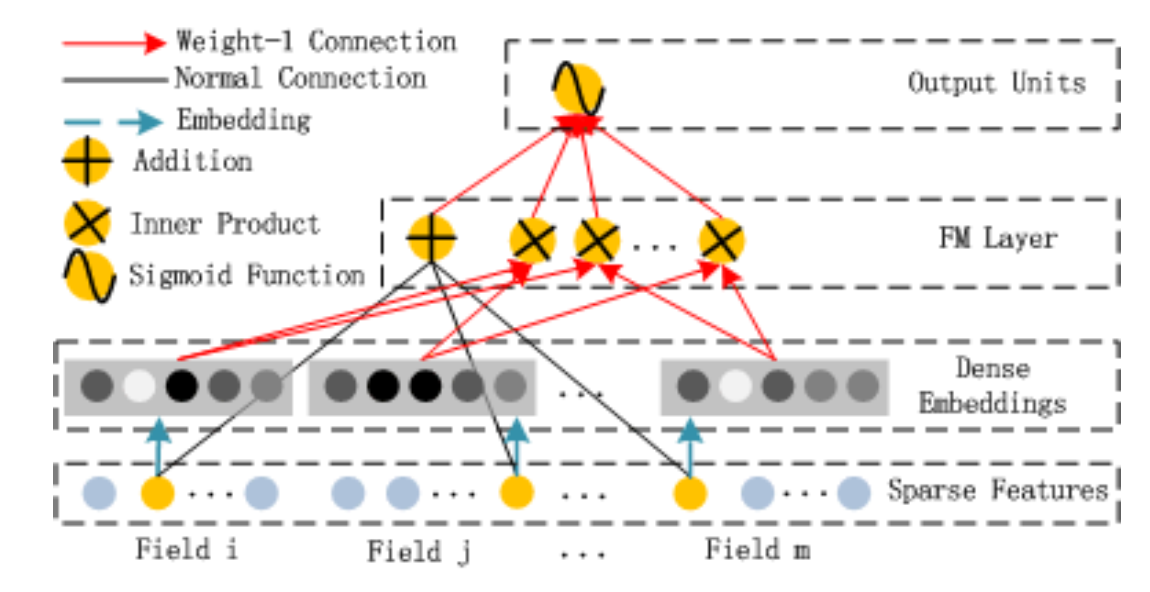
上图是FM组件，它实现的就是：

\[ y_{FM}=\langle w, x \rangle + \sum_{i=1}^d \sum_{j=i+1}^d \langle V_i, V_j \rangle x_i \cdot x_j \]

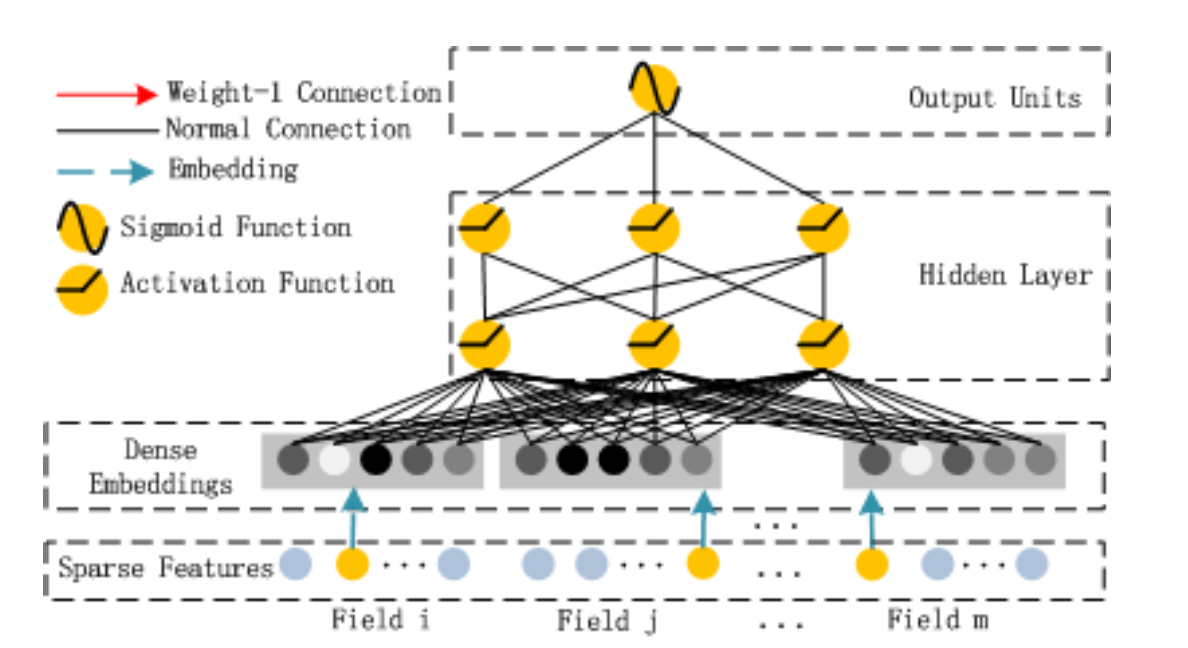
上图即为DNN组件，也非常简单，不过我们需要记得它的Embedding要和前面的FM共享。

代码

数据处理

def data_process(data, categorical_cols, numerical_cols):
    """数据处理"""
    label_encoder = LabelEncoder()
    for col in categorical_cols:
        data[col] = data[col].fillna("-1")
        data[col] = label_encoder.fit_transform(data[col])
    for col in numerical_cols:
        data[col] = data[col].fillna(0.)
        data[col] = data[col].astype(np.float32)
        data[col] = data[col].apply(lambda x: np.log(x+1) if x > -1 else -1)
    return data

Linear

@tf.function
def call(self, inputs):
    categorical_inputs, numerical_inputs = inputs
    outputs = 0.
    for cat_input, cat_weight in zip(categorical_inputs, self._categorical_weights):
        sparse_w = K.dot(cat_input, cat_weight)
        outputs += sparse_w
    if numerical_inputs:
        numerical_inputs = K.concatenate(numerical_inputs)
        outputs += K.dot(numerical_inputs, self._numerical_weights)
    return outputs

这个函数的作用就是线性部分$\langle w, x \rangle$。

Embedding

def build(self, input_shape):
    categorical_shapes, numerical_shapes = input_shape
    self._categorical_weights = [
        self.add_weight(
            shape=(cat_shape[-1], self._embedding_dim),
            initializer=initializers.glorot_uniform,
            regularizer=self._regularizer,
            trainable=self._trainable,
            name=f'categorical_weights_{i}'
        ) for i, cat_shape in enumerate(categorical_shapes)]
    if self._numerical_embedding is True:
        self._numerical_weights = [
            self.add_weight(
                shape=(1, self._embedding_dim),
                initializer=initializers.glorot_uniform,
                regularizer=self._regularizer,
                trainable=self._trainable,
                name=f'numerical_weights_{i}'
            ) for i in range(len(numerical_shapes))]
      super(Embedding, self).build(input_shape)

@tf.function
def call(self, inputs):
    categorical_inputs, numerical_inputs = inputs
    categorical_embeddings = []
    for cat_input, cat_weight in zip(categorical_inputs, self._categorical_weights):
        cat_embed = K.dot(cat_input, cat_weight)
        categorical_embeddings.append(cat_embed)
    if self._numerical_embedding is True:
        numerical_embeddings = []
        for num_input, num_weight in zip(numerical_inputs, self._numerical_weights):
            num_embed = K.dot(num_input, num_weight)
            numerical_embeddings.append(num_embed)
        embeddings = (categorical_embeddings, numerical_embeddings)
    else:
        embeddings = (categorical_embeddings, numerical_inputs)
    return embeddings

对Categorical的每一个filed特征做固定大小的embedding，这里是4；对于连续特征可以做embedding，也可以直接用原值。

FM

@tf.function
def call(self, inputs):
    categorical_inputs, numerical_inputs = inputs
    if categorical_inputs and numerical_inputs and \
            categorical_inputs[0].shape[-1] != numerical_inputs[0].shape[-1] \
            and self._numerical_interactive is True:
        raise ValueError('If `fm_numerical_interactive` is True, '
                         'categorical_inputs`s shape must equals to numerical_inputs`s shape')
    if self._numerical_interactive is True:
        exp_inputs = [K.expand_dims(x, axis=1) for x in categorical_inputs+numerical_inputs]
    else:
        exp_inputs = [K.expand_dims(x, axis=1) for x in categorical_inputs]
    concat_inputs = K.concatenate(exp_inputs, axis=1)
    square_inputs = K.square(K.sum(concat_inputs, axis=1))
    sum_inputs = K.sum(K.square(concat_inputs), axis=1)
    cross_term = square_inputs - sum_inputs
    outputs = 0.5 * K.sum(cross_term, axis=1, keepdims=True)
    return outputs

这里计算有个小技巧，不需要用for循环。对于三个向量C1,C2和C3，需要把c1的Embedding向量𝑉𝑐1、𝑉𝑐2和𝑉𝑐3的两两内积：

\[ \sum_{i=1}^d \sum_{j=i+1}^d \langle V_i, V_j \rangle x_i \cdot x_j = \langle V_{c_1}, V_{c_2} \rangle +\langle V_{c_1}, V_{c_3} \rangle + \langle V_{c_2}, V_{c_3} \rangle \]

但是这怎么用矩阵乘法一次计算出来呢？我们可以看看这个：

\[ x_1x_2 + x_1x_3 + x_2x_3 = \frac{1}{2}[(x_1+x_2+x_3)^2 -(x_1^2+x_2^2+x_3^2) ] \]

因此我们可以把Embedding后的向量加起来，然后平方然后减去每一个向量的平方(内积)，再除以2。

DNN和输出

DNN层就不写了，需要注意FM的输入和DNN的输入都是同一个embedding。输出则是将这两部分合并后接sigmoid。

@tf.function
def call(self, inputs):
    outputs = K.concatenate(inputs, axis=1)
    outputs = K.sum(outputs, axis=1, keepdims=True)
    outputs = K.sigmoid(outputs)
    return outputs

reference

DeepFM模型CTR预估理论与实战

TF 2.0 Keras 实现 DeepFM