1. 基本概念

• 方向导数：是一个数；反映的是f(x,y)在P0点沿方向v的变化率。
• 偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。
• 偏导函数：是一个函数；是一个关于点的偏导数的函数。
• 梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。

2. 方向导数

反映的是f(x,y)在P0点沿方向v的变化率。

例子如下：

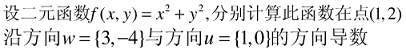
方向导数计算公式

偏导数

二元函数偏导数的几何意义

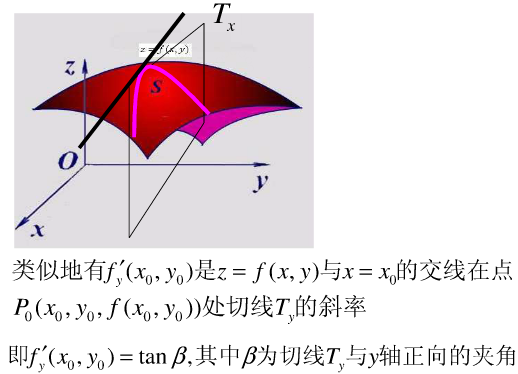
偏导函数

偏导数与偏导函数的关系：

偏导数是偏导函数在指定点的函数值，因此在求偏导数时，也可先求出偏导函数，然后再将点代入偏导函数，从而求出函数在此点的偏导数。

3. 全微分

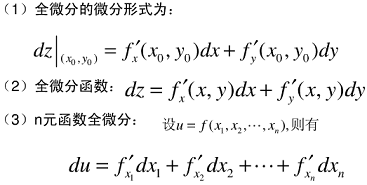
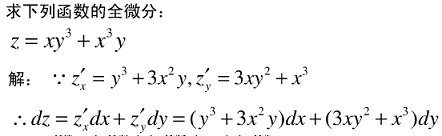
4. 梯度

梯度是一个向量；既有大小，也有方向。

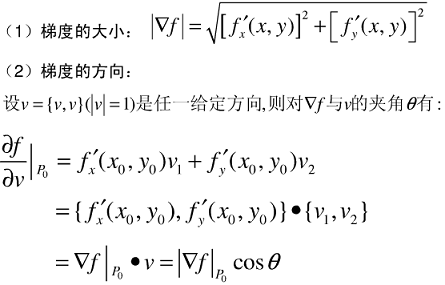
几何意义

函数z=f(x,y)在点P0处的梯度方向是函数变化率(即方向导数)最大的方向。

梯度的方向就是函数f(x,y)在这点增长最快的方向，梯度的模为方向导数的最大值。