GBDT (Gradient Boosting Decision Tree) 是另一种基于 Boosting 思想的集成算法，除此之外 GBDT 还有很多其他的叫法，例如：GBM (Gradient Boosting Machine)，GBRT (Gradient Boosting Regression Tree)，MART (Multiple Additive Regression Tree) 等等。GBDT 算法由 3 个主要概念构成：Gradient Boosting (GB)，Regression Decision Tree (DT 或 RT) 和 Shrinkage。

0. Decision Tree：CART回归树

首先，GBDT使用的决策树是CART回归树，无论是处理回归问题还是二分类以及多分类，GBDT使用的决策树通通都是都是CART回归树。为什么不用CART分类树呢？因为GBDT每次迭代要拟合的是梯度值，是连续值所以要用回归树。对于回归树算法来说最重要的是寻找最佳的划分点，那么回归树中的可划分点包含了所有特征的所有可取的值。在分类树中最佳划分点的判别标准是熵或者基尼系数，都是用纯度来衡量的，但是在回归树中的样本标签是连续数值，所以再使用熵之类的指标不再合适，取而代之的是平方误差，它能很好的评判拟合程度。

回归树生成算法：

输入：训练数据集$D$

输出：回归树$f ( x )$

在训练数据集所在的输入空间中，递归的将每个区域划分为两个子区域并决定每个子区域上的输出值，构建二叉决策树：

（1）选择最优切分变量$j \(与切分点$s\)，求解

遍历变量$j$，对固定的切分变量$j$扫描切分点$s$，选择使得上式达到最小值的对$( j , s )$

（2）用选定的对$( j , s ) $划分区域并决定相应的输出值：

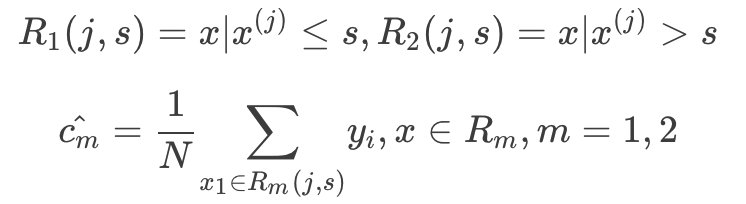
（3）继续对两个子区域调用步骤（1）和（2），直至满足停止条件。

（4）将输入空间划分为$M$个区域 $R_1 , R_2 , . . . R_M $，生成决策树：

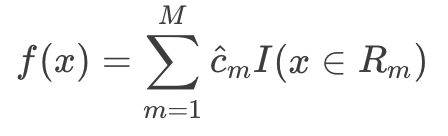
例子：

训练数据见下表，x的取值范围为区间[0.5,10.5]，y的取值范围为区间[5.0,10.0]，学习这个回归问题的最小二叉回归树。

求解训练数据的切分点s:

\[ R_1=\{x|x\leq s\}\ \ \ \ \ \ \ R_2=\{x|x>s\} \]

容易求得在$R_1$、$R_2$内部使得平方损失误差达到最小值的c1、c2为：

\[ c_1=\frac{1}{N_1}\sum_{x_i\in R_1}y_i \ \ \ \ c_2=\frac{1}{N_2}\sum_{x_i\in R_2}y_i \]

这里$N_1$、$N_2$是$R_1$、$R_2$的样本点数。

求训练数据的切分点，根据所给数据，考虑如下切分点：

1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5。

对各切分点，不难求出相应的$R_1、R_2、c_1、c_2$及

\[ m(s)=\mathop{min}\limits_{j,s}\left[\mathop{min}\limits_{c_1}\sum_{x_i\in R_1(j,s)}(y_i-c_1)^{2}+\mathop{min}\limits_{c_2}\sum_{x_i\in R_2(j,s)}(y_i-c_2)^{2}\right] \]

例如，当s=1.5时，$R_1={1}$，$R_2={2,3,...,10}$，$c_1=5.56，c_2=7.50$，则

\[ m(s)=\mathop{min}\limits_{j,s}\left[\mathop{min}\limits_{c_1}\sum_{x_i\in R_1(j,s)}(y_i-c_1)^{2}+\mathop{min}\limits_{c_2}\sum_{x_i\in R_2(j,s)}(y_i-c_2)^{2}\right]=0+15.72 = 15.72 \]

现将s及m(s)的计算结果列表如下：

由上表可知，当x=6.5的时候达到最小值，此时$R_1={1,2,...,6}$，$R_2={7,8,9,10}$，$c_1=6.24$，$c_2=8.9$，所以回归树T1(x)为：

\[ T_1(x)=\left\{ \begin{aligned} 6.24, & x<6.5 \\ 8.91, &x\geq6.5 \end{aligned} \right.\\f_1(x)=T_1(x) \]

用$f_1(x)$拟合训练数据的残差见下表，表中$r_i=y_i-f_1(x_i),i=1,2,...,10$

第2步求$T_2(x)$方法与求$T_1(x)$一样，只是拟合的数据是上表的残差，可以得到：

\[ T_2(x)=\left\{ \begin{aligned} -0.52, & x<3.5 \\ 0.22, &x\geq3.5 \end{aligned} \right.\\f_2(x)=T_2(x)+f_1(x)=\left\{ \begin{aligned} 5.72, & x<3.5 \\ 6.46, &3.5\leq x<6.5\\ 9.13, &x\geq 6.5 \end{aligned} \right. \]

继续求得

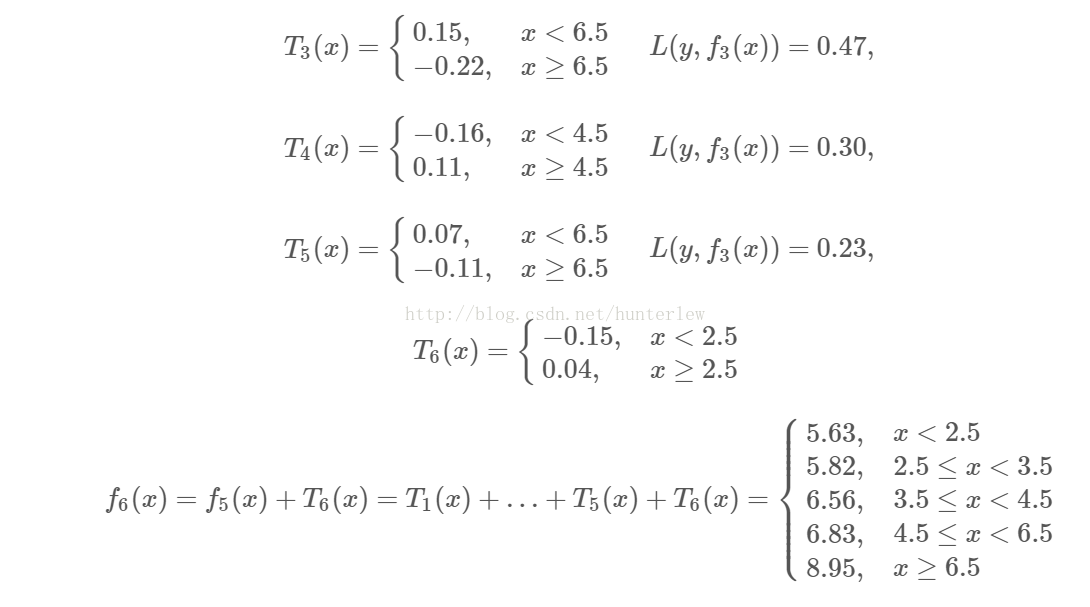
可以用拟合训练数据的平方损失误差等来作为结束条件。此时

假设此时已经满足误差要求，那么f(x)=f6(x)即为所求的回归树。

1. GBDT概述

GBDT也是集成学习Boosting家族的成员，但是却和传统的Adaboost有很大的不同。回顾下Adaboost，我们是利用前一轮迭代弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去。GBDT也是迭代，使用了前向分布算法，但是弱学习器限定了只能使用CART回归树模型，同时迭代思路和Adaboost也有所不同。

对于 Gradient Boosting 而言，首先，Boosting 并不是 Adaboost 中 Boost 的概念，也不是 Random Forest 中的重抽样。在 Adaboost 中，Boost 是指在生成每个新的基学习器时，根据上一轮基学习器分类对错对训练集设置不同的权重，使得在上一轮中分类错误的样本在生成新的基学习器时更被重视。GBDT 中在应用 Boost 概念时，每一轮所使用的数据集没有经过重抽样，也没有更新样本的权重，而是每一轮选择了不同的回归目标，即上一轮计算得到的残差 (Residual)。其次，Gradient 是指在新一轮中在残差减少的梯度 (Gradient) 上建立新的基学习器。

在GBDT的迭代中，假设我们前一轮迭代得到的强学习器是$f_{t−1}(x)$, 损失函数是$L(y,f_{t−1}(x))$, 我们本轮迭代的目标是找到一个CART回归树模型的弱学习器$h_t(x)$，让本轮的损失函数$L(y,f_t(x))=L(y,f_{t−1}(x)+h_t(x))$最小。也就是说，本轮迭代找到决策树，要让样本的损失尽量变得更小。

GBDT的思想可以用一个通俗的例子解释，假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。

从上面的例子看这个思想还是蛮简单的，但是有个问题是这个损失的拟合不好度量，损失函数各种各样，怎么找到一种通用的拟合方法呢？

2. GBDT的负梯度拟合

在上一节中，我们介绍了GBDT的基本思路，但是没有解决损失函数拟合方法的问题。针对这个问题，大牛Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值，进而拟合一个CART回归树。第t轮的第i个样本的损失函数的负梯度表示为

\[ r_{ti} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]_{f(x) = f_{t-1} (x)} \]

利用$(x_i,r_{ti})(i=1,2,..m)$,我们可以拟合一颗CART回归树，得到了第t颗回归树，其对应的叶节点区域$R_{tj},j=1,2,...,J$。其中J为叶子节点的个数。

针对每一个叶子节点里的样本，我们求出使损失函数最小，也就是拟合叶子节点最好的的输出值$c_{tj}$如下：

\[ c_{tj} = \underbrace{arg\; min}_{c}\sum\limits_{x_i \in R_{tj}} L(y_i,f_{t-1}(x_i) +c) \]

这样就得到了本轮的决策树拟合函数如下：

\[ h_t(x) = \sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj}) \]

从而本轮最终得到的强学习器的表达式如下：

\[ f_{t}(x) = f_{t-1}(x) + \sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj}) \]

通过损失函数的负梯度来拟合，我们找到了一种通用的拟合损失误差的办法，这样无轮是分类问题还是回归问题，我们通过其损失函数的负梯度的拟合，就可以用GBDT来解决我们的分类回归问题。区别仅仅在于损失函数不同导致的负梯度不同而已。

3. GBDT回归算法

好了，有了上面的思路，下面我们总结下GBDT的回归算法。为什么没有加上分类算法一起？那是因为分类算法的输出是不连续的类别值，需要一些处理才能使用负梯度，我们在下一节讲。

输入是训练集样本$T=\{(x_1,y_1),(x_2,y_2),...(x_m,y_m)\}$，最大迭代次数T, 损失函数L。

输出是强学习器$f(x)$

1) 初始化弱学习器（常数c）

\[ f_0(x) = \underbrace{arg\; min}_{c}\sum\limits_{i=1}^{m}L(y_i, c) \]

2) 对迭代轮数t=1,2,...T有：

3) 得到强学习器f(x)的表达式

\[ f(x) = f_T(x) =f_0(x) + \sum\limits_{t=1}^{T}\sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj}) \]

4. GBDT分类算法

再看看GBDT分类算法，GBDT的分类算法从思想上和GBDT的回归算法没有区别，但是由于样本输出不是连续的值，而是离散的类别，导致我们无法直接从输出类别去拟合类别输出的误差。

为了解决这个问题，主要有两个方法，一个是用指数损失函数，此时GBDT退化为Adaboost算法。另一种方法是用类似于逻辑回归的对数似然损失函数的方法。也就是说，我们用的是类别的预测概率值和真实概率值的差来拟合损失。本文仅讨论用对数似然损失函数的GBDT分类。而对于对数似然损失函数，我们又有二元分类和多元分类的区别。

4.1 二元GBDT分类算法

对于二元GBDT，如果用类似于逻辑回归的对数似然损失函数，则损失函数为：

\[ L(y, f(x)) = log(1+ exp(-yf(x))) \]

其中$𝑦∈\{−1,+1\}$。则此时的负梯度误差为

\[ r_{ti} = -\bigg[\frac{\partial L(y, f(x_i)))}{\partial f(x_i)}\bigg]_{f(x) = f_{t-1}\;\; (x)} = \frac{y_i}{(1+exp(y_if(x_i)))} \]

对于生成的决策树，各个叶子节点的最佳负梯度拟合值为

\[ c_{tj} = \underbrace{arg\; min}_{c}\sum\limits_{x_i \in R_{tj}} log(1+exp(-y_i(f_{t-1}(x_i) +c))) \]

由于上式比较难优化，我们一般使用近似值代替

\[ c_{tj} = \sum\limits_{x_i \in R_{tj}}r_{ti}\bigg / \sum\limits_{x_i \in R_{tj}}|r_{ti}|(1-|r_{ti}|) \]

除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，二元GBDT分类和GBDT回归算法过程相同。

4.2 多元GBDT分类算法

多元GBDT要比二元GBDT复杂一些，对应的是多元逻辑回归和二元逻辑回归的复杂度差别。假设类别数为K，则此时我们的对数似然损失函数为：

\[ L(y, f(x)) = - \sum\limits_{k=1}^{K}y_klog\;p_k(x) \]

其中如果样本输出类别为k，则$𝑦_𝑘=1$。第k类的概率$𝑝_𝑘(𝑥)$的表达式为：

\[ p_k(x) = exp(f_k(x)) \bigg / \sum\limits_{l=1}^{K} exp(f_l(x)) \]

集合上两式，我们可以计算出第𝑡轮的第𝑖个样本对应类别𝑙的负梯度误差为

\[ r_{til} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]_{f_k(x) = f_{l, t-1}\;\; (x)} = y_{il} - p_{l, t-1}(x_i) \]

观察上式可以看出，其实这里的误差就是样本$i$对应类别$l$的真实概率和$t−1$轮预测概率的差值。

对于生成的决策树，我们各个叶子节点的最佳负梯度拟合值为

\[ c_{tjl} = \underbrace{arg\; min}_{c_{jl}}\sum\limits_{i=0}^{m}\sum\limits_{k=1}^{K} L(y_k, f_{t-1, l}(x) + \sum\limits_{j=0}^{J}c_{jl} I(x_i \in R_{tjl})) \]

由于上式比较难优化，我们一般使用近似值代替

\[ c_{tjl} = \frac{K-1}{K} \; \frac{\sum\limits_{x_i \in R_{tjl}}r_{til}}{\sum\limits_{x_i \in R_{til}}|r_{til}|(1-|r_{til}|)} \]

除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，多元GBDT分类和二元GBDT分类以及GBDT回归算法过程相同。

GBDT（梯度提升树）