背景

随着预训练语言模型进入LLM时代，其参数量愈发庞大。全量微调模型所有参数所需的显存早已水涨船高。

例如：

全参微调Qwen1.5-7B-Chat预估要2张80GB的A800，160GB显存
全参微调Qwen1.5-72B-Chat预估要20张80GB的A800，至少1600GB显存。
而且，通常不同的下游任务还需要LLM的全量参数，对于算法服务部署来说简直是个灾难

当然，一种折衷做法就是全量微调后把增量参数进行SVD分解保存，推理时再合并参数

为了寻求一个不更新全部参数的廉价微调方案，之前一些预训练语言模型的高效微调(Parameter Efficient finetuning, PEFT)工作，要么插入一些参数或学习外部模块来适应新的下游任务。

Adapter tuning

Adapter Tuning试图在Transformer Layer的Self-Attetion+FFN之后插入一个先降维再升维的MLP（以及一层残差和LayerNormalization）来学习模型微调的知识。

在预训练模型每一层(或某些层)中添加Adapter模块(如上图左侧结构所示)，微调时冻结预训练模型主体，由Adapter模块学习特定下游任务的知识。每个Adapter模块由两个前馈子层组成，第一个前馈子层将Transformer块的输出作为输入，将原始输入维度d投影到m，通过控制m的大小来限制Adapter模块的参数量，通常情况下m<<d。在输出阶段，通过第二个前馈子层还原输入维度，将m重新投影到d，作为Adapter模块的输出(如上图右侧结构)。通过添加Adapter模块来产生一个易于扩展的下游模型，每当出现新的下游任务，通过添加Adapter模块来避免全模型微调与灾难性遗忘的问题。Adapter方法不需要微调预训练模型的全部参数，通过引入少量针对特定任务的参数，来存储有关该任务的知识，降低对模型微调的算力要求。

缺点：需要修改原有模型结构，同时还会增加模型参数量。

Adapter算法改进

2020年，Pfeiffer J等人对Adapter进行改进，「提出AdapterFusion算法，用以实现多个Adapter模块间的最大化任务迁移」(其模型结构如下图所示)。

AdapterFusion将学习过程分为两个阶段：

● 1.「知识提取阶段」：训练Adapter模块学习下游任务的特定知识，将知识封装在Adapter模块参数中。

● 2.「知识组合阶段」：将预训练模型参数与特定于任务的Adapter参数固定，引入新参数学习组合多个Adapter中的知识，提高模型在目标任务中的表现。

其中首先，对于N个不同的下游任务训练N个Adapter模块。然后使用AdapterFusion组合N个适配器中的知识，将预训练参数$Θ$ 和全部的Adapter参数 $Φ$ 固定，引入新的参数 $Ψ$，使用N个下游任务的数据集训练，让AdapterFusion学习如何组合N个适配器解决特定任务。参数 $Ψ$ 在每一层中包含Key、Value和Query（上图右侧架构所示）。在Transformer每一层中将前馈网络子层的输出作为Query，Value和Key的输入是各自适配器的输出，将Query和Key做点积传入SoftMax函数中，根据上下文学习对适配器进行加权。在给定的上下文中，AdapterFusion学习经过训练的适配器的参数混合，根据给定的输入识别和激活最有用的适配器。（像MoE）

「作者通过将适配器的训练分为知识提取和知识组合两部分，解决了灾难性遗忘、任务间干扰和训练不稳定的问题。Adapter模块的添加也导致模型整体参数量的增加，降低了模型推理时的性能」。

Adapter Fusion 在 Adapter 的基础上进行优化，通过将学习过程分为两阶段来提升下游任务表现。作者对全模型微调(Full)、Adapter、AdapterFusion三种方法在各个数据集上进行和对比试验。AdapterFusion在大多数情况下性能优于全模型微调和Adapter，特别在MRPC(相似性和释义任务数据集)与RTE(识别文本蕴含数据集)中性能显著优于另外两种方法。

Promot Tuning

Prompt Tuning设计了一种prefix prompt方法，即在模型输入的token序列前添加前缀prompt token，而这个前缀prompt token的embedding是由网络学到。

Prompt Tuning可以看做token已经确定，但是embedding是可以学的。

它相当于仅用prompt token的embedding去适应下游任务，相比手工设计或挑选prompt，它是一种Soft的prompt(软提示)

给定𝑛个token组成的输入序列 ${{x}{1} , {x}{2}, \ldots,{x}_{n}}$ ，其对应token embedding矩阵为 $\mathbf{X}_{e} \in \mathbb{R}^{n \times d}$，𝑑代表嵌入维度。

Soft-prompts对应参数$\mathbf{P}_{e} \in \mathbb{R}^{p \times d}$，𝑝 代表prompt的长度。

然后，将prompt拼接到输入前面，就能得到完整的模型输入 $[\mathbf{P}_{e} ; \mathbf{X}_{e}] \in \mathbb{R}^{(p+n) \times d}$。

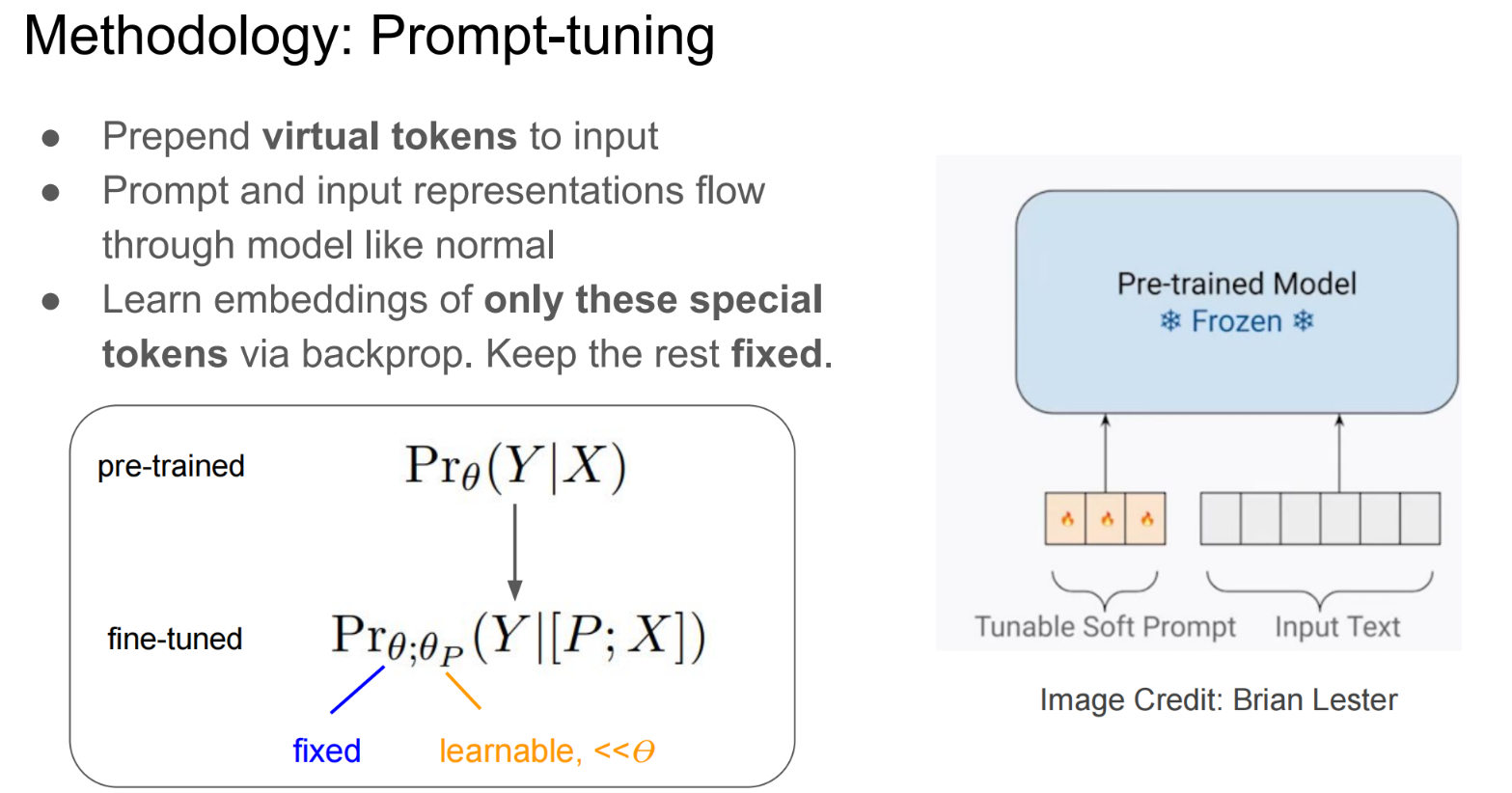
这个新的输入将会送入模型$f([\mathbf{P}; \mathbf{X}]; \Theta, \Theta_{p})$，以最大化交叉熵损失来最大化条件概率 $Pr_{\Theta, \Theta_{p}}(\mathbf{Y} | [\mathbf{P}; \mathbf{X}])$，以拟合其标签token序列 𝑌。

在针对下游任务微调时，Prompt Tuning将冻结原始LLM的参数，只学习独立的prompt token参数（参数化的prompt token加上输入的token送入模型进行前向传播，反向传播只更新prompt token embedding的参数）。

在针对不同的下游任务微调时，就可以分别学习不同的Task Specifical的Prompt Token参数。

Soft Prompt Tuning在模型增大时可以接近Model Tuning(fine-tuning)的效果
离散Prompt Tuning(Prompt Design)基本不能达到Model Tuning的效果

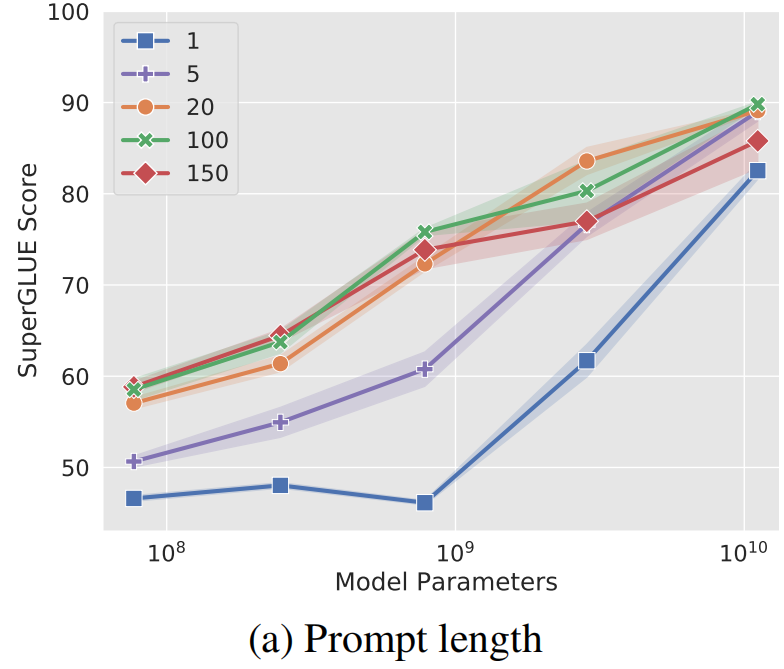
Promot Tuning方法的参数成本是 𝑒𝑑，其中 𝑒 是提示长度，𝑑是token嵌入维度。提示越短，必须调整的新参数就越少，那么调参的目标是就是找到表现仍然良好的最小prefix prompt长度。

Promot Tuning在输入序列前缀添加连续可微的软提示作为可训练参数，其缺点在于：由于模型可接受的最大输入长度有限，随着软提示的参数量增多，实际输入序列的最大长度也会相应减小，影响模型性能。

Prefix-Tuning

为了避免人为的离散Prompt选取优化，Prefix-Tuning提出可学习的Prefix Prompt

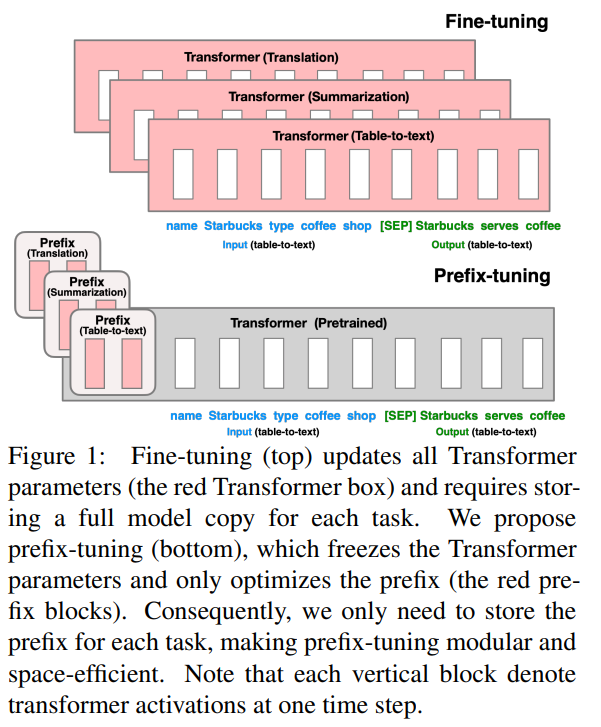
Prefix-Tuning提出可学习的Prompt，即：

learns a sequence of prefixes that are prepended at every transformer layer

Prefix tuning为𝑙层的Transformer Layer的每层多头注意力的键和值都配置了可学习的prefix vectors.

Two sets of prefix vectors $\mathbf{P}_{k}$,$\mathbf{P}_{v} \in \mathbb{R}^{l\times d}$ are concatenated with the original key 𝐾 and value 𝑉

\[ \mathrm{head}_i=\mathrm{Attn}(\boldsymbol{xW}_q^{(i)},\mathrm{concat}(\boldsymbol{P}_k^{(i)},\boldsymbol{CW}_k^{(i)}),\mathrm{concat}(\boldsymbol{P}_v^{(i)},\boldsymbol{CW}_v^{(i)})) \]

看到这里可以知道，Prefix-Tuning可以算是Promot Tuning的一个特例（Promot Tuning只在输入侧加入可学习的Prefix Prompt Token，Prefix-Tuning推广到Transformer Layer每一层的K、V上）

LoRA

LoRA（Low-Rank Adaptation of LLMs），即LLMs的低秩适应，被提出用于高效参数微调。

LoRA的核心思想，是假设LLM在下游任务上微调得到的增量参数矩阵 $Δ𝑊$ 是低秩的，即是存在冗余参数的高维矩阵，但实际有效矩阵是更低维度的。

相关论文表明训练学到的过度参数化的模型实际上存在于一个较低的内在维度上。类似于机器学习中的降维算法，假设高维数据实际是在低维的流形上一样。

Lora架构

左侧为全参数微调，右侧为Lora微调

全参数微调会优化LLM的所有参数。这相当于在LLM的原始权重 $\mathbf{W}_{0} \in \mathbb{R}^{d \times d}$ 上，加上一个了微调增量参数$\Delta \mathbf{W} \in \mathbb{R}^{d \times d} $（相当于冻结原始权重，插入增量参数并仅对做优化）。

对于全参数微调后的LLM权重，给定输入𝑥，其输出为下式：

\[ \mathbf{h} = (\mathbf{W}_{0} + \Delta \mathbf{W} ) \mathbf{x} = \mathbf{W}_{0}\mathbf{x} + \Delta \mathbf{W}\mathbf{x} \]

既然，对增量参数矩阵 $Δ𝑊$有低秩假设。

那么在微调LLM时，完全可以对每一层的参数，加入参数$𝐵$ 和 $𝐴$ 对增量参数 $Δ𝑊$ 进行来低秩近似，同时只训练参数$𝐵$ 和 $𝐴$。这就是上图右侧的Lora微调。

这样一来，在微调过程中，可训练的参数量大大减少（使得微调参数量从 𝑑×𝑑 降低至 2𝑟𝑑 , 有 𝑟<<𝑑 ）

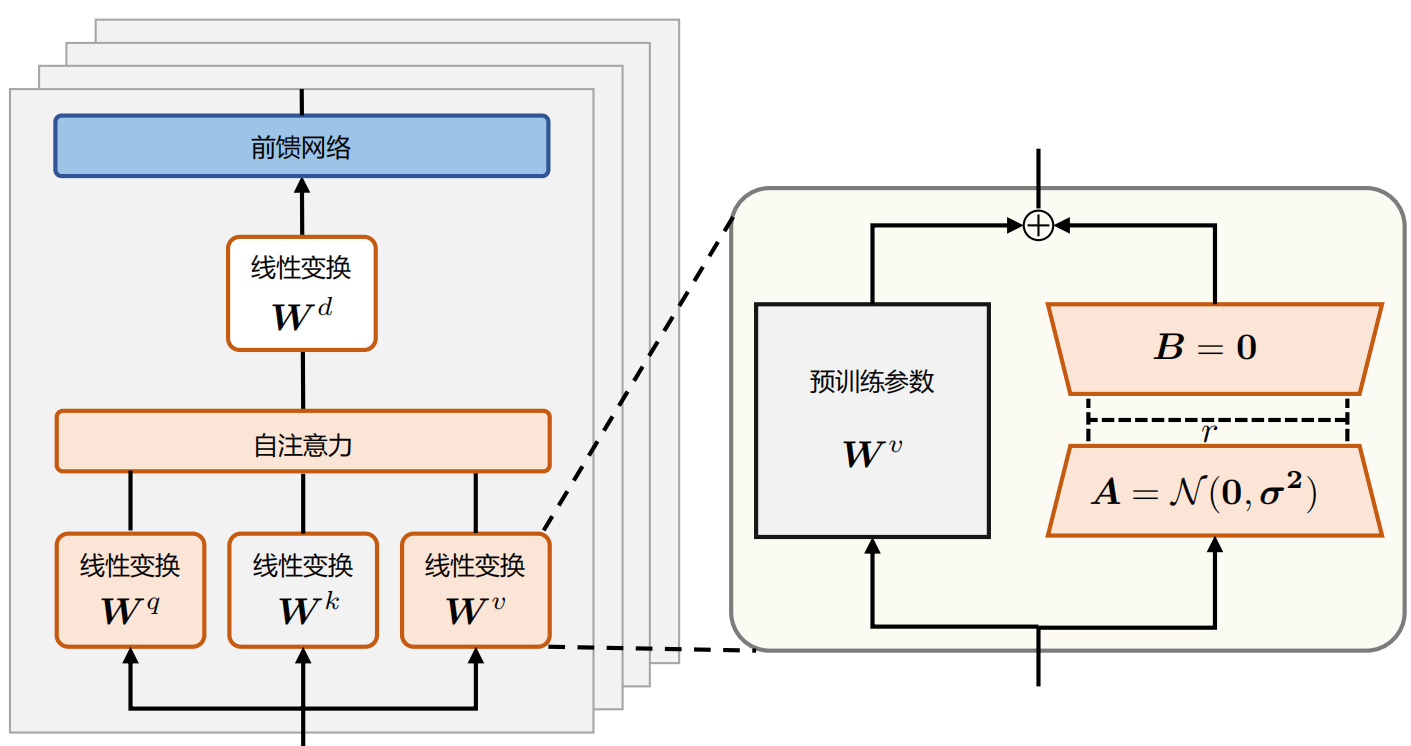
具体来说，LoRA将$\Delta \mathbf{W} = \mathbf{B} \mathbf{A} \in \mathbb{R}^{d \times d} $ 用两个更小的参数矩阵进行低秩近似，其中 $𝑟$ 是LoRA的需要近似$Δ𝑊$ 的秩的维度，$\mathbf{B}\in \mathbb{R}^{d\times r}$ 和 $\mathbf{A}\in \mathbb{R}^{r \times d}$。

在LoRA微调时，冻结预训练的模型权重 $\mathbf{W}_{0} \in \mathbb{R}^{d \times d}$，并将可训练的LoRA低秩分解矩阵注入到LLM的每个Transformer Decoder层中。在训练时，只优化所有的 𝐵 和 𝐴 矩阵，从而大大减少了下游任务的可训练参数量。

对于该权重的输入𝑥来说，输出为下式：

\[ \mathbf{h} = (\mathbf{W}_{0} + \Delta \mathbf{W} ) \mathbf{x} = \mathbf{W}_{0}\mathbf{x} + \mathbf{B}\mathbf{A} \mathbf{x} \]

LoRA参数初始化时，矩阵 $𝐴$ 通过高斯函数初始化。矩阵 𝐵 为全零初始化，其目的是希望训练开始之前旁路对原模型不造成影响（带来噪声），即参数改变量为0。

对于使用LoRA的模型来说，由于可以将原权重与训练后权重合并，因此在推理时不存在额外的开销。