背景

随着预训练语言模型进入LLM时代，其参数量愈发庞大。全量微调模型所有参数所需的显存早已水涨船高。

例如：

全参微调Qwen1.5-7B-Chat预估要2张80GB的A800，160GB显存
全参微调Qwen1.5-72B-Chat预估要20张80GB的A800，至少1600GB显存。
而且，通常不同的下游任务还需要LLM的全量参数，对于算法服务部署来说简直是个灾难

当然，一种折衷做法就是全量微调后把增量参数进行SVD分解保存，推理时再合并参数

为了寻求一个不更新全部参数的廉价微调方案，之前一些预训练语言模型的高效微调(Parameter Efficient finetuning, PEFT)工作，要么插入一些参数或学习外部模块来适应新的下游任务。

LoRA

LoRA（Low-Rank Adaptation of LLMs），即LLMs的低秩适应，被提出用于高效参数微调。

LoRA的核心思想，是假设LLM在下游任务上微调得到的增量参数矩阵 $Δ𝑊$ 是低秩的，即是存在冗余参数的高维矩阵，但实际有效矩阵是更低维度的。

相关论文表明训练学到的过度参数化的模型实际上存在于一个较低的内在维度上。类似于机器学习中的降维算法，假设高维数据实际是在低维的流形上一样。

Lora架构

左侧为全参数微调，右侧为Lora微调

全参数微调会优化LLM的所有参数。这相当于在LLM的原始权重 $\mathbf{W}_{0} \in \mathbb{R}^{d \times d}$ 上，加上一个了微调增量参数$\Delta \mathbf{W} \in \mathbb{R}^{d \times d} $（相当于冻结原始权重，插入增量参数并仅对做优化）。

对于全参数微调后的LLM权重，给定输入𝑥，其输出为下式：

\[ \mathbf{h} = (\mathbf{W}_{0} + \Delta \mathbf{W} ) \mathbf{x} = \mathbf{W}_{0}\mathbf{x} + \Delta \mathbf{W}\mathbf{x} \]

既然，对增量参数矩阵 $Δ𝑊$有低秩假设。

那么在微调LLM时，完全可以对每一层的参数，加入参数$𝐵$ 和 $𝐴$ 对增量参数 $Δ𝑊$ 进行来低秩近似，同时只训练参数$𝐵$ 和 $𝐴$。这就是上图右侧的Lora微调。

这样一来，在微调过程中，可训练的参数量大大减少（使得微调参数量从 𝑑×𝑑 降低至 2𝑟𝑑 , 有 𝑟<<𝑑 ）

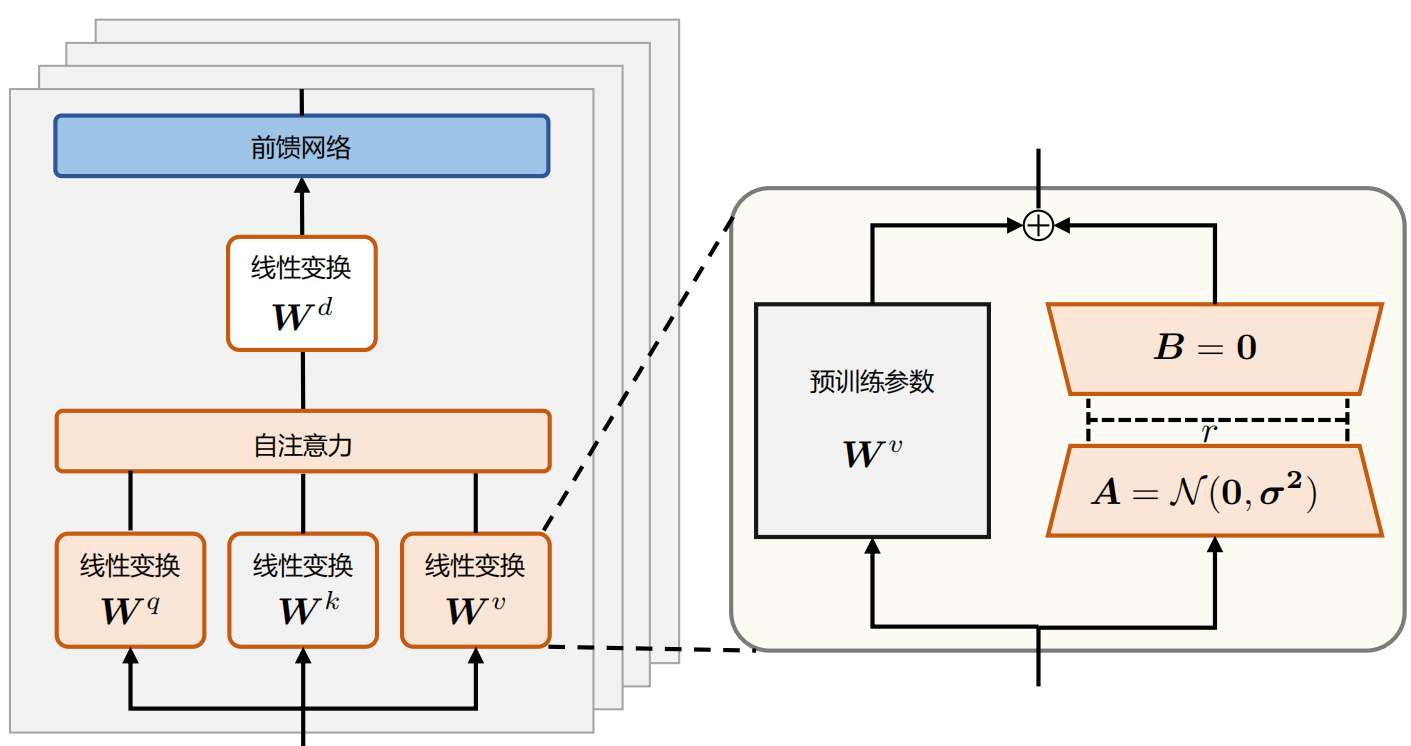
具体来说，LoRA将$\Delta \mathbf{W} = \mathbf{B} \mathbf{A} \in \mathbb{R}^{d \times d} $ 用两个更小的参数矩阵进行低秩近似，其中 $𝑟$ 是LoRA的需要近似$Δ𝑊$ 的秩的维度，$\mathbf{B}\in \mathbb{R}^{d\times r}$ 和 $\mathbf{A}\in \mathbb{R}^{r \times d}$。

在LoRA微调时，冻结预训练的模型权重 $\mathbf{W}_{0} \in \mathbb{R}^{d \times d}$，并将可训练的LoRA低秩分解矩阵注入到LLM的每个Transformer Decoder层中。在训练时，只优化所有的 𝐵 和 𝐴 矩阵，从而大大减少了下游任务的可训练参数量。

对于该权重的输入𝑥来说，输出为下式：

\[ \mathbf{h} = (\mathbf{W}_{0} + \Delta \mathbf{W} ) \mathbf{x} = \mathbf{W}_{0}\mathbf{x} + \mathbf{B}\mathbf{A} \mathbf{x} \]

LoRA参数初始化时，矩阵 $𝐴$ 通过高斯函数初始化。矩阵 𝐵 为全零初始化，其目的是希望训练开始之前旁路对原模型不造成影响（带来噪声），即参数改变量为0。

对于使用LoRA的模型来说，由于可以将原权重与训练后权重合并，因此在推理时不存在额外的开销。

LST

论文地址

🔖 https://papers.cool/arxiv/2206.06522

论文提出了一个新的名为“Ladder Side-Tuning（LST）”的训练技巧，它号称同时达到了参数高效和训练高效。是否真有这么理想的“过墙梯”？

这里借用此文中的配图，来说明一下，在LORA之前的常见的Memory Efficient Transfer Learning方法。

反向传播，也就是求模型梯度，是从输出层向输入层逐步计算的，因此反向传播的深度/计算量，取决于最靠近输入层的参数深度，跟可训练的参数量没有太必然的联系。对于Adapter来说，它在每一层后面都插入了一个小规模的层，虽然其余参数都固定了，只有新插入的层可训练，但每一层都新层，所以反向传播要传到输入层；对于P-tuning来说，本质上它是只有在Embedding层中有少量可训练参数，但Embedding层是输入层，因此它的反向传播也要贯穿整个模型。因此，这两种方案能提升的训练效率并不多。

至于LST，它是在原有大模型的基础上搭建了一个“旁支”（梯子），将大模型的部分层输出作为旁枝模型的输入，所有的训练参数尽在旁枝模型中，由于大模型仅提供输入，因此反向传播的复杂度取决于旁枝模型的规模，并不需要直接在原始大模型上执行反向传播，因此是可以明显提升训练效率的。

实验效果

原论文做了不少LST的实验，包括NLP、CV的，下面是LST在GLUE数据集上的效果：

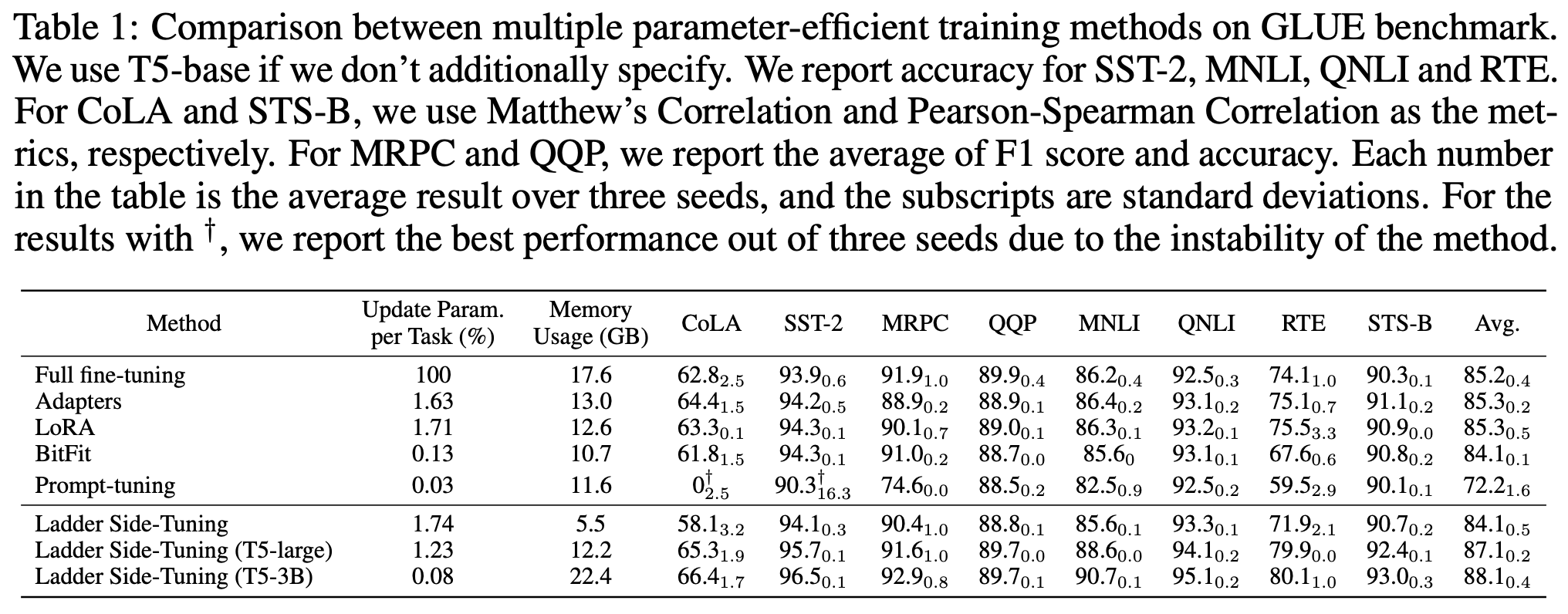
可以看到，LST确实具备了参数高效和训练高效的特点，能够在较小的训练参数和训练成本的情况下，达到一个不错的微调效果。特别是最后两行的实验结果，体现出了LST在有限训练资源下微调大模型的可能性。

与LORA的区别

LST与LORA类似，在原有参数矩阵的一侧增加了一个旁支通路，但是二者有些许区别：

LORA是将上一步的输入，在分支的时候，分别经过原有参数（类似于图中蓝色部分），以及旁支的通路（绿色可训练参数），二者之间是类似平等的，然后再将结果相加，作为下一层的输入；
LST是在将输入先经过原有参数，再与输入本身相加，一起送入旁支通路。

PEFT对LORA的实现

接下来是代码部分，我们以HF的PEFT（当前版本0.2.0）为例，介绍一下LORA是如何作用在HF模型上的。

以LORA为例，PEFT模型的使用非常方便，只需要按照原本的方式实例化模型，然后设置一下LORA的config，调用一下get_peft_model方法，就获得了在原模型基础上的PEFT模型，对于LORA策略来讲，就是在某些参数矩阵W的基础上增加了矩阵分解的旁支。在下面的例子中，选择了attention中的q和v的部分做LORA。

# 设置超参数及配置
LORA_R = 8
LORA_ALPHA = 16
LORA_DROPOUT = 0.05
TARGET_MODULES = [
    "q_proj",
    "v_proj",
]

config = LoraConfig(
    r=LORA_R,
    lora_alpha=LORA_ALPHA,
    target_modules=TARGET_MODULES,
    lora_dropout=LORA_DROPOUT,
    bias="none",
    task_type="CAUSAL_LM",
)

# 创建基础transformer模型
model = AutoModelForSeq2SeqLM.from_pretrained(model_name_or_path)
# 加入PEFT策略
model = get_peft_model(model, config)

简单介绍一下Lora config相关的配置：

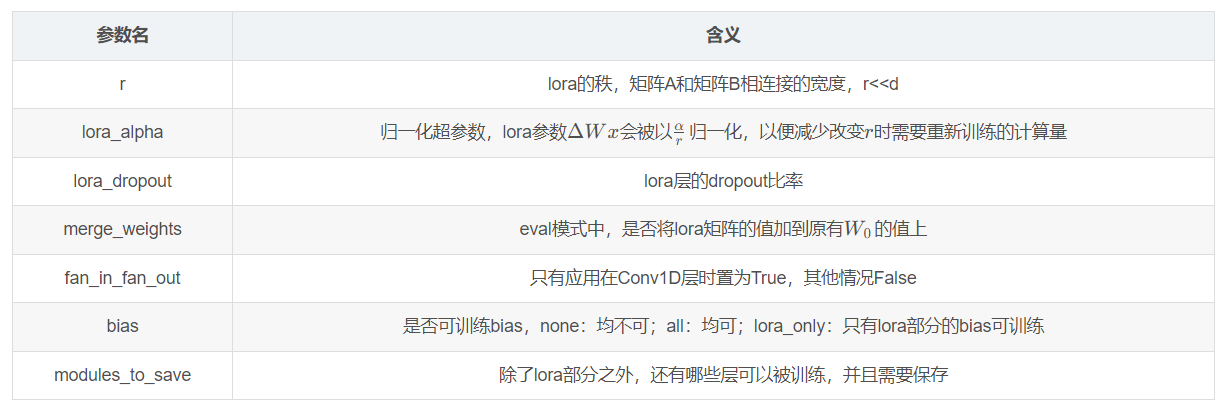
具体参数可参考：

🔖 https://huggingface.co/docs/peft/package_reference/lora#peft.LoraConfig

接下来，结合PEFT模块的源码，来看一下LORA是如何实现的。

在PEFT模块中，peft_model.py中的PeftModel类是一个总控类，用于模型的读取保存等功能，继承了transformers中的Mixin类，我们主要来看LORA的实现：

上面是比较新的代码，已经融合了很多的方法，并且做了很多工程化的东西，读起来比较复杂，这里就看比较早之前的一份代码

class LoraModel(torch.nn.Module):
    def __init__(self, config, model):
        super().__init__()
        self.peft_config = config
        self.model = model
        self._find_and_replace()
        mark_only_lora_as_trainable(self.model, self.peft_config.bias)
        self.forward = self.model.forward

从构造方法可以看出，这个类在创建的时候主要做了两件事：

_find_and_replace：找到所有需要加入lora策略的层，例如q_proj，把它们替换成lora模式；
保留lora部分的参数可训练，其余参数全都固定下来不动。
_find_and_replace的逻辑很清晰，就是先找到需要的做lora的层，然后创建lora层把它替换掉。这里把关键语句列出如下：

找目标层：

# 其中的target_modules在上面的例子中就是"q_proj"，"v_proj"
# 这一步就是找到模型的各个组件中，名字里带"q_proj"，"v_proj"的
target_module_found = re.fullmatch(self.peft_config.target_modules, key)

然后对于每一个找到的目标层，创建一个新的lora层：

# 注意这里的Linear是在该py中新建的类，不是torch的Linear
new_module = Linear(target.in_features, target.out_features, bias=bias, **kwargs)

最后调用_replace_module方法替换掉原来的linear：

self._replace_module(parent, target_name, new_module, target)

其中这个replace的方法并不复杂，就是把原来的weight和bias赋给新创建的module，然后再分配到指定的设备上：

def _replace_module(self, parent_module, child_name, new_module, old_module):
    setattr(parent_module, child_name, new_module)
    new_module.weight = old_module.weight
    if old_module.bias is not None:
        new_module.bias = old_module.bias
    if getattr(old_module, "state", None) is not None:
        new_module.state = old_module.state
        new_module.to(old_module.weight.device)

    # dispatch to correct device
    for name, module in new_module.named_modules():
        if "lora_" in name:
            module.to(old_module.weight.device)

接下来主要看一下Lora层的实现，首先是Lora的基类，可以看出这个类就是用来构造Lora的各种超参数用：

class LoraLayer:
    def __init__(
        self,
        r: int,
        lora_alpha: int,
        lora_dropout: float,
        merge_weights: bool,
    ):
        self.r = r
        self.lora_alpha = lora_alpha
        # Optional dropout
        if lora_dropout > 0.0:
            self.lora_dropout = nn.Dropout(p=lora_dropout)
        else:
            self.lora_dropout = lambda x: x
        # Mark the weight as unmerged
        self.merged = False
        self.merge_weights = merge_weights
        self.disable_adapters = False

然后就要讲到上文中所提到的Linear类，也就是Lora的具体实现，它同时继承了nn.Linear和LoraLayer。

class Linear(nn.Linear, LoraLayer):
    # Lora implemented in a dense layer
    def __init__(
        self,
        in_features: int,
        out_features: int,
        r: int = 0,
        lora_alpha: int = 1,
        lora_dropout: float = 0.0,
        fan_in_fan_out: bool = False,  # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
        merge_weights: bool = True,
        **kwargs,
    ):
        nn.Linear.__init__(self, in_features, out_features, **kwargs)
        LoraLayer.__init__(self, r=r, lora_alpha=lora_alpha, lora_dropout=lora_dropout, merge_weights=merge_weights)

        self.fan_in_fan_out = fan_in_fan_out
        # Actual trainable parameters
        if r > 0:
            self.lora_A = nn.Linear(in_features, r, bias=False)
            self.lora_B = nn.Linear(r, out_features, bias=False)
            self.scaling = self.lora_alpha / self.r
            # Freezing the pre-trained weight matrix
            self.weight.requires_grad = False
        self.reset_parameters()
        if fan_in_fan_out:
            self.weight.data = self.weight.data.T

在构造方法中，除了对各个超参数进行配置之外，还对所有参数进行了初始化，定义如下：

    def reset_parameters(self):
        nn.Linear.reset_parameters(self)
        if hasattr(self, "lora_A"):
            # initialize A the same way as the default for nn.Linear and B to zero
            nn.init.kaiming_uniform_(self.lora_A.weight, a=math.sqrt(5))
            nn.init.zeros_(self.lora_B.weight)

其中lora的A矩阵采用了kaiming初始化，是Xavier初始化针对非线性激活函数的一种优化；B矩阵采用了零初始化，以确保在初始状态 $ \Delta W =BA$ 为零。（值得注意的是在LORA的论文中，A采用的是Gaussian初始化）。

对于train和eval方法，放在一起介绍，它主要是需要对merge状态进行记录：

def train(self, mode: bool = True):
    nn.Linear.train(self, mode)
    self.lora_A.train(mode)
    self.lora_B.train(mode)
    if not mode and self.merge_weights and not self.merged:
        # Merge the weights and mark it
        if self.r > 0:
            self.weight.data += (
                transpose(self.lora_B.weight @ self.lora_A.weight, self.fan_in_fan_out) * self.scaling
            )
        self.merged = True
    elif self.merge_weights and self.merged:
        # Make sure that the weights are not merged
        if self.r > 0:
            self.weight.data -= (
                transpose(self.lora_B.weight @ self.lora_A.weight, self.fan_in_fan_out) * self.scaling
            )
        self.merged = False

def eval(self):
    nn.Linear.eval(self)
    self.lora_A.eval()
    self.lora_B.eval()

首先对于新定义的这个Linear层，其本身继承了torch.nn.Linear，所以需要调用nn.Linear.train(self, mode)来控制一下自身原本参数的状态，并且此外它加入了lora_A和lora_B两部分额外的参数，这两部分本质上也是nn.Linear，也需要控制状态。

然后主要来理解一下merge_weights是在做什么，也就是看train中的if分支，not mode说明是eval模式，而self.merge_weights在上文中有介绍，是配置文件中的，意思是评估时是否需要将lora部分的weight加到linear层原本的weight中，not self.merged是状态的记录，也就是说，如果设置了需要融合，而当前状态没有融合的话，就把lora部分的参数scale之后加上去，并且更新self.merged状态；在elif分支中，是为了在训练的过程中，确保linear本身的weights是没有经过融合过的（理论上这一步应该是在eval之后的下一轮train的第一个step触发）。

至于为什么是在train中涉及merge_weights，其实在torch的源码中，nn.Linear.eval()实际上是调用了nn.Linear.train(mode=False)，所以这里train方法中的merge_weigths，实际上是在eval中也发挥作用的。

forward中也是类似的原理，正常情况下训练过程应该是走elif的分支：

def forward(self, x: torch.Tensor):
    if self.disable_adapters:
        if self.r > 0 and self.merged:
            self.weight.data -= (
                transpose(self.lora_B.weight @ self.lora_A.weight, self.fan_in_fan_out) * self.scaling
            )
            self.merged = False

        return F.linear(x, transpose(self.weight, self.fan_in_fan_out), bias=self.bias)
    elif self.r > 0 and not self.merged:
        result = F.linear(x, transpose(self.weight, self.fan_in_fan_out), bias=self.bias)
        if self.r > 0:
            result += self.lora_B(self.lora_A(self.lora_dropout(x))) * self.scaling
        return result
    else:
        return F.linear(x, transpose(self.weight, self.fan_in_fan_out), bias=self.bias)

在了解了这些基本原理之后，就可以类似地去实现更多更加灵活的功能了，例如对transformer的某些层增加lora，而其余的层保持不变等。

Reference

🔖 https://blog.csdn.net/weixin_44826203/article/details/129733930

🔖 https://kexue.fm/archives/9138