对于向量的三维旋转问题，给定旋转轴和旋转角度，用罗德里格斯（Rodrigues）旋转公式可以得出旋转后的向量。另外，罗德里格斯旋转公式可以用旋转矩阵表示，即将三维旋转的轴-角（axis-angle）表示转变为旋转矩阵表示。

向量投影（Vector projection）

向量a在非零向量b上的向量投影指的是a在平行于向量b的直线上的正交投影。结果是一个平行于b的向量，定义为 $\mathbf{a}_1=a_1\hat{\mathbf{b}}$，其中，$\mathbf{a}_1$ 是一个标量，称为a在b上的标量投影，$\hat{\mathbf{b}}$ 是与 b 同向的单位向量。$a_1=\left\Vert\mathbf{a}\right\Vert\cos\theta=\mathbf{a}\cdot \hat{\mathbf{b}}=\mathbf{a}\cdot\frac{\mathbf{b}}{\left\Vert\mathbf{b}\right\Vert}$，其中$\cdot$ 表示点积(又称标量积)，$\left\Vert\mathbf{a}\right\Vert$表示a的长度，$\theta$ 表示a和b的夹角。标量投影有正负，正负号与夹角 $\theta$ 有关。

有了向量投影$\mathbf{a}_1$ ，向量 a 可以表示为$\mathbf{a}=\mathbf{a}_1+\mathbf{a}_2$ ，其中 $\mathbf{a}_2$ 称为a from b的vector rejection（没找到比较官方的翻译），也即a 向正交于 b 的超平面的正交投影，$\mathbf{a}_2=\mathbf{a}-\mathbf{a}_1=\mathbf{a}-(\left\Vert\mathbf{a}\right\Vert\cos\theta)\hat{\mathbf{b}}$。下图比较清晰地表示出$\mathbf{a}$, $\mathbf{a}_1$,$\mathbf{a}_2$的关系。

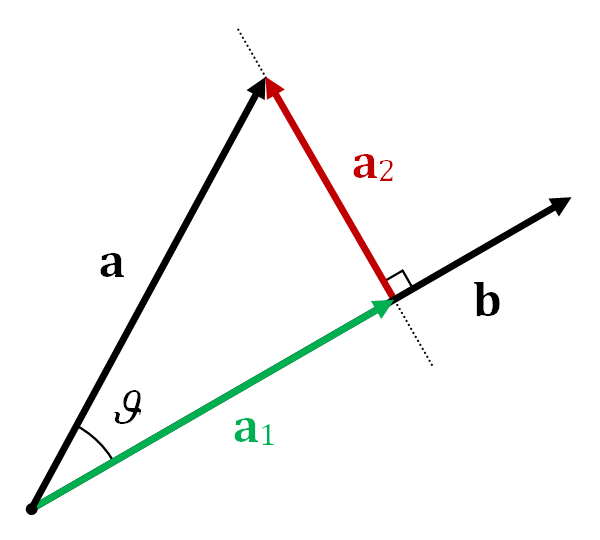
当$90^{\circ}<\theta\le180^{\circ}$ 时，向量投影示意图如图2所示：

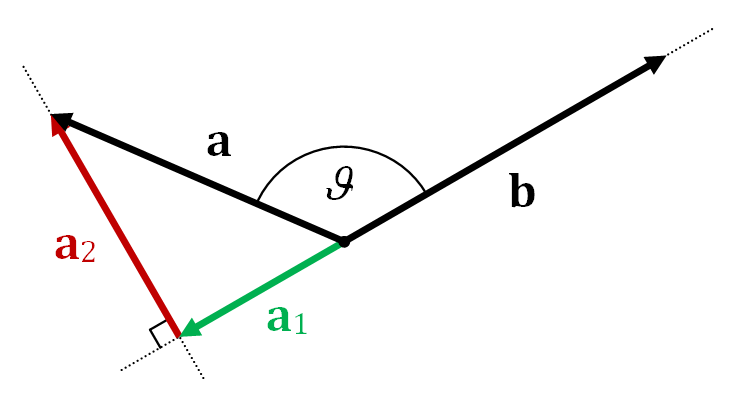
记号

向量a在b上的向量投影用加粗的$\mathbf{a}_1$表示，标量投影用不加粗的$a_1$。有时向量投影和vector rejection分别用$\mathbf{a}_{\parallel\mathbf{b}}$和$\mathbf{a}_{\perp\mathbf{b}}$表示。

用a和b表示

当$\theta$ 未知时，可通过a和b计算得出，$\cos\theta = \frac{\mathbf{a}\cdot\mathbf{b}}{\left\Vert\mathbf{a}\right\Vert\left\Vert\mathbf{b}\right\Vert}$，从而标量投影、向量投影和vector rejection可以分别表示如下：

标量投影：
$$
\begin{equation}
a_1=\left\Vert\mathbf{a}\right\Vert\cos\theta=\left\Vert\mathbf{a}\right\Vert\frac{\mathbf{a}\cdot\mathbf{b}}{\left\Vert\mathbf{a}\right\Vert\left\Vert\mathbf{b}\right\Vert}=\frac{\mathbf{a}\cdot\mathbf{b}}{\left\Vert\mathbf{b}\right\Vert}
\end{equation}
$$
向量投影：
$$
\begin{equation}
\mathbf{a}_1=a_1\hat{\mathbf{b}}=\frac{\mathbf{a}\cdot\mathbf{b}}{\left\Vert\mathbf{b}\right\Vert}\frac{\mathbf{b}}{\left\Vert\mathbf{b}\right\Vert}=\left(\mathbf{a}\cdot\hat{\mathbf{b}}\right)\hat{\mathbf{b}}=\frac{\mathbf{a}\cdot\mathbf{b}}{\mathbf{b}\cdot\mathbf{b}}\mathbf{b}
\end{equation}
$$
vector rejection：
$$
\begin{equation}
\mathbf{a}_2=\mathbf{a}-\mathbf{a}_1=\mathbf{a}-\frac{\mathbf{a}\cdot\mathbf{b}}{\mathbf{b}\cdot\mathbf{b}}\mathbf{b}
\end{equation}
$$

叉积

定义

叉积（又称向量积）是三维空间（$\mathbb{R}^3$）向量的二元操作，用符号 × 表示，给定两个线性独立的向量a和b，叉积$\mathbf{a}\times\mathbf{b}$ 的结果是一个向量，这个向量与a、b都正交，也就是正交于a、b所在的平面。为什么要强调线性独立呢，因为非线性独立的两个向量（同向或反向）的叉积为0。

叉积定义为：

\[ \begin{equation} \mathbf{a}\times\mathbf{b}=\left\Vert\mathbf{a}\right\Vert\left\Vert\mathbf{b}\right\Vert\sin(\theta)\mathbf{n} \end{equation} \]

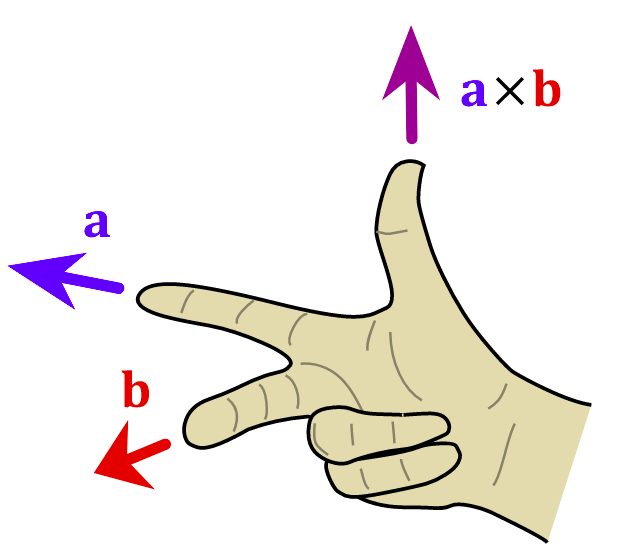
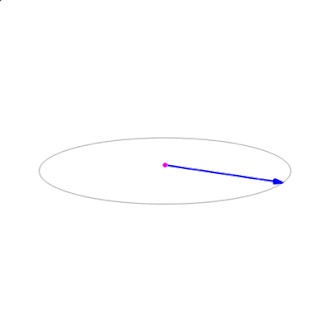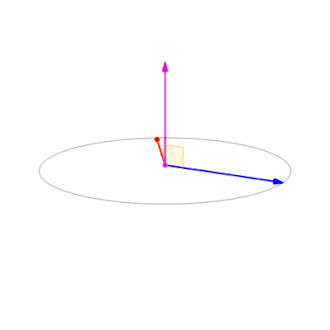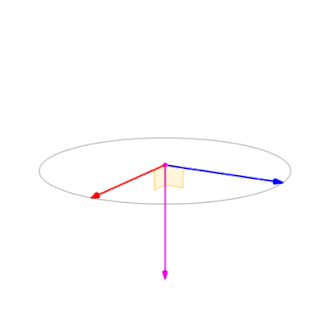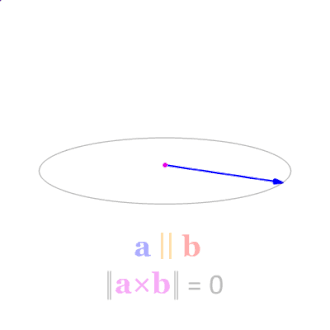
其中，$\theta$ 表示a、b的夹角，$0^\circ\le\theta\le180^\circ$，$\mathbf{n}$ 正交于a、b所在的平面，方向通常由右手法则确定，如下图所示：

性质

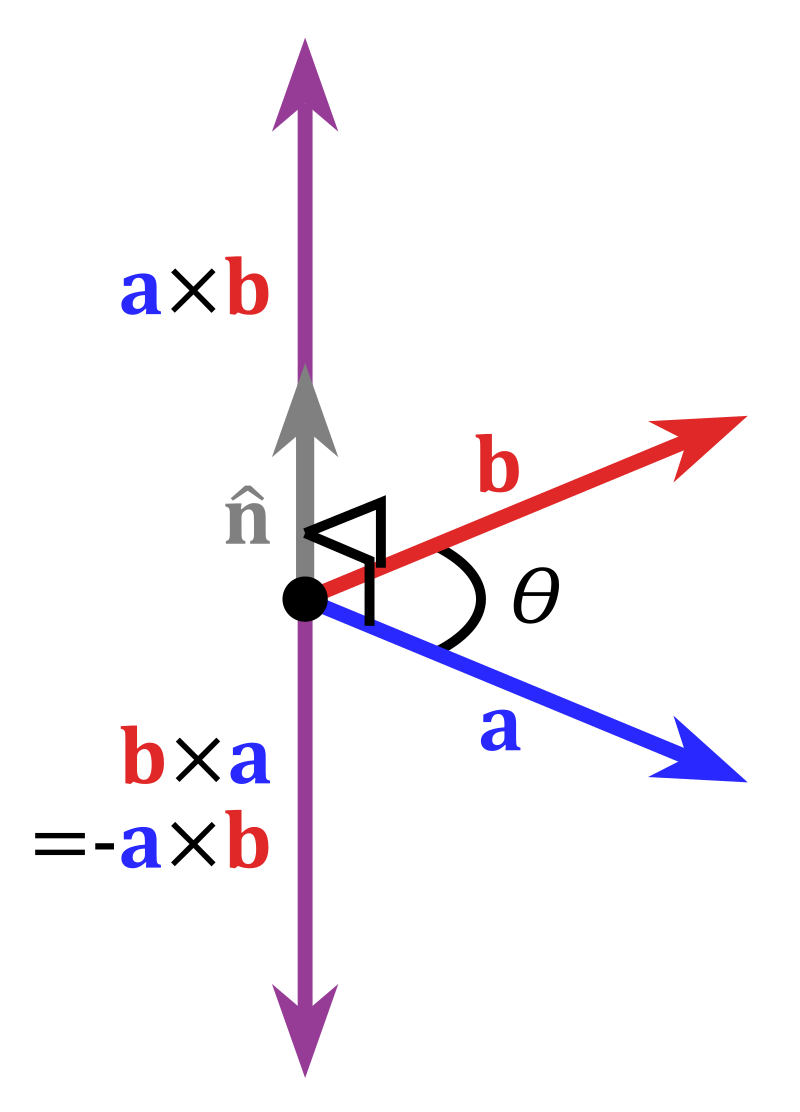
右手法则决定了叉积不符合交换律，而符合反交换律，即$\mathbf{a}\times\mathbf{b}=-\mathbf{b}\times\mathbf{a}$，如图4所示：

由公式也可以看出当a、b不线性独立时，即夹角为$0^\circ$或$180^\circ$时，叉积为零向量0。叉积随夹角$\theta$ 的变化如图5所示。

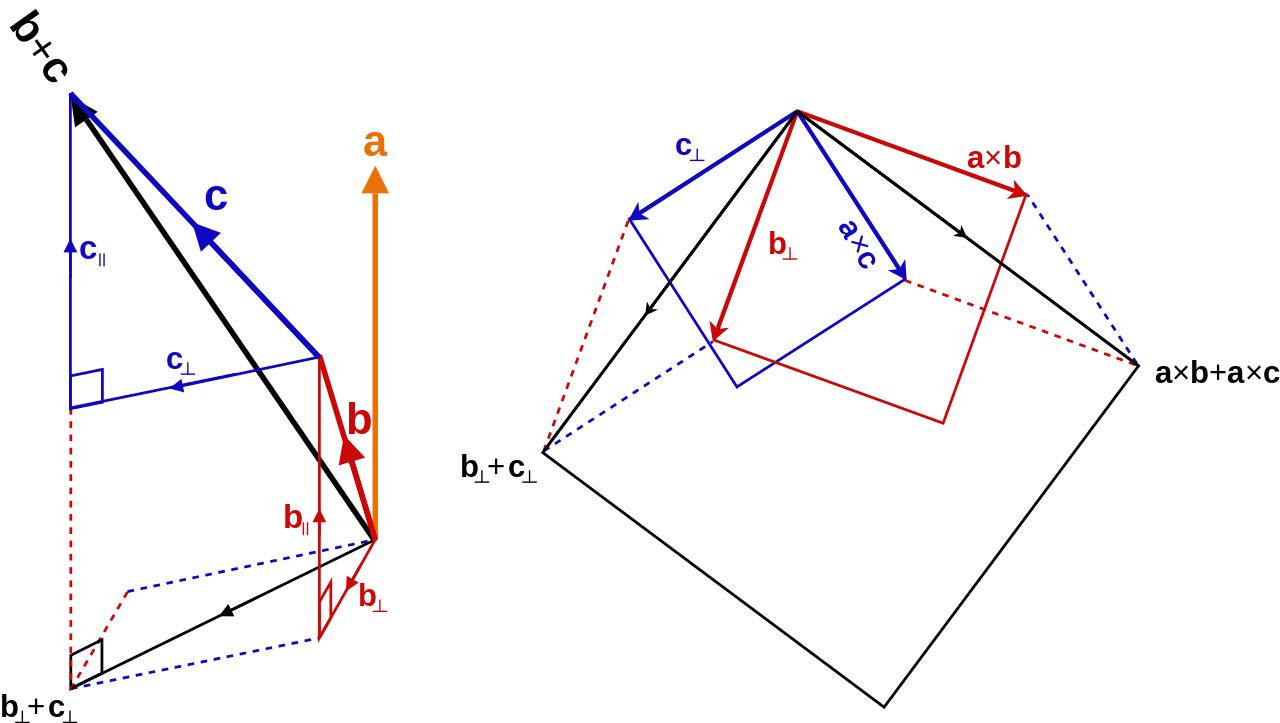
另外，叉积符合分配律，即$\mathbf{a}\times(\mathbf{b}+\mathbf{c})=\mathbf{a}\times\mathbf{b}+\mathbf{a}\times\mathbf{c}$。如图6所示，左图向量b和c都被分解为vector projection和vector rejection两部分，右图则解释了分配律成立的原因，看图时要注意图中的平行四边形和正方形都表示了相等的关系。

坐标表示

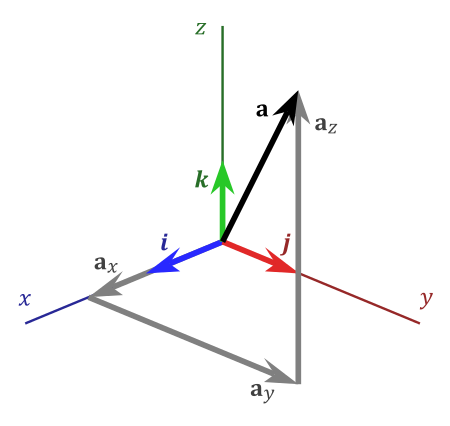
考虑右手法则定义的标准三维坐标系，三个坐标轴$\mathbf{i}$、$\mathbf{j}$、$\mathbf{k}$如图7所示，并满足以下等式关系：

\[ \mathbf{i}\times\mathbf{j}=\mathbf{k}\\ \mathbf{j}\times\mathbf{k}=\mathbf{i}\\ \mathbf{k}\times\mathbf{i}=\mathbf{j} \]

同样，由叉积的反交换律可得下面三个等式关系：

\[ \mathbf{j}\times\mathbf{i}=-\mathbf{k}\\ \mathbf{k}\times\mathbf{j}=-\mathbf{i}\\ \mathbf{i}\times\mathbf{k}=-\mathbf{j} \]

由平行向量的叉积为零向量可得：$\mathbf{i}\times\mathbf{i}=\mathbf{j}\times\mathbf{j}=\mathbf{k}\times\mathbf{k}=\mathbf{0}$。

由图7也可得，任意一个三维向量都可以表示为三个基向量的线性组合，例如：

\[ \mathbf{a}=a_1\mathbf{i}+a_2\mathbf{j}+a_3\mathbf{k}\\ \mathbf{b}=b_1\mathbf{i}+b_2\mathbf{j}+b_3\mathbf{k} \]

进而，可以用坐标表示叉积运算如下：

\[ \begin{equation} \begin{split} \mathbf{a}\times\mathbf{b}&=(a_1\mathbf{i}+a_2\mathbf{j}+a_3\mathbf{k})\times(b_1\mathbf{i}+b_2\mathbf{j}+b_3\mathbf{k})\\ &=(a_2b_3-a_3b_2)\mathbf{i}+(a_3b_1-a_1b_3)\mathbf{j}+(a_1b_2-a_2b_1)\mathbf{k}\\ &=\left|\begin{array}{cccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{array}\right| \end{split} \end{equation} \]

上式中，将括号展开分别进行叉积推导出第二个等号，而第三个等号则可通过行列式计算得出。

进一步，可将叉积表示为矩阵与向量相乘的形式，由于$\mathbf{a}\times\mathbf{b}=(a_2b_3-a_3b_2, a_3b_1-a_1b_3,a_1b_2-a_2b_1)$，则叉积可表示为：

\[ \begin{equation} \begin{split} \mathbf{a}\times\mathbf{b}=\left[\mathbf{a}\right]_\times\mathbf{b}=\left[\begin{array}{cccc} 0 & -a_3 & a_2\\ a_3 & 0 & -a_1\\ -a_2 & a_1 & 0 \end{array} \right]\left[ \begin{array}{cc} b_1\\b_2\\b_3 \end{array}\right]=\left[\mathbf{b}\right]^T_\times\mathbf{a}=\left[\begin{array}{cccc} 0 & b_3 & -b_2\\ -b_3 & 0 & b_1\\ b_2 & -b_1 & 0 \end{array} \right]\left[ \begin{array}{cc} a_1\\a_2\\a_3 \end{array}\right] \end{split} \end{equation} \]

其中，$\left[\mathbf{a}\right]_\times$表示由向量 $\mathbf{a}$ 得到的反对称矩阵$A^T=-A$，定义为：

\[ \begin{equation} \begin{split} \left[\mathbf{a}\right]_\times=\left[\begin{array}{cccc} 0 & -a_3 & a_2\\ a_3 & 0 & -a_1\\ -a_2 & a_1 & 0 \end{array} \right] \end{split} \end{equation} \]

通过该反对称矩阵的定义可以将叉积表示为矩阵与向量的乘法。

罗德里格斯旋转公式

考虑$\mathbf{v}\in\mathbb{R}^3$ 的三维旋转问题，旋转轴$\mathbf{k}$ 是单位向量，旋转角为$\theta$，按照右手法则（即逆时针）旋转。则可通过罗德里格斯旋转公式得出旋转后的向量$\mathbf{v}_{rot}$为：

\[ \begin{equation} \mathbf{v}_{rot}=\cos\theta\mathbf{v}+(1-\cos\theta)(\mathbf{k}\cdot\mathbf{v})\mathbf{k}+\sin\theta\mathbf{k}\times\mathbf{v} \end{equation} \]

推导过程

由上文中向量投影部分的知识我们知道，一个向量$\mathbf{v}$可以分解为平行于$\mathbf{k}$的分量$\mathbf{v}_\parallel$和正交于$\mathbf{k}$的分量$\mathbf{v}_{\perp}$：

\[ \begin{equation} \mathbf{v}=\mathbf{v}_{\parallel}+\mathbf{v}_\perp \end{equation} \]

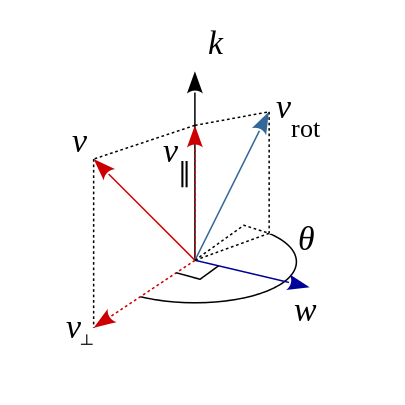
如图8所示，因为$\mathbf{k}$ 为单位向量，由向量投影部分知识可得

\[ \begin{equation} \mathbf{v}_\parallel=(\mathbf{v}\cdot\mathbf{k})\mathbf{k} \end{equation} \]

\[ \begin{equation} \mathbf{v}_\perp=\mathbf{v}-\mathbf{v}_\parallel=\mathbf{v}-(\mathbf{k}\cdot\mathbf{v})\mathbf{k}=-\mathbf{k}\times(\mathbf{k}\times\mathbf{v}) \end{equation} \]

式(11)用于后面推导维基百科中罗德里格斯旋转公式的矩阵形式，其中，最后一个等号的推导如下：

回顾叉积的知识，$\mathbf{k}\times\mathbf{v}=\mathbf{k}\times(\mathbf{v}_{\parallel}+\mathbf{v}_\perp)=\mathbf{0}+\mathbf{k}\times\mathbf{v}_\perp=\mathbf{k}\times\mathbf{v}_\perp$，$\mathbf{k}\times\mathbf{v}$ 可以看做将$\mathbf{v}_{\perp}$以$\mathbf{k}$ 为旋转轴逆时针旋转了 $90^\circ$(可参考图8理解)。正如图9所示，$\mathbf{v}$分解为$\mathbf{v}_\parallel$和$\mathbf{v}_{\perp}$，用右手法则不难确定出$\mathbf{k}\times\mathbf{v}$ 的方向，进而不难发现，$\mathbf{k}\times(\mathbf{k}\times\mathbf{v})$ 可以看做将$\mathbf{v}_{\perp}$以$\mathbf{k}$ 为旋转轴逆时针旋转了$180^\circ$，图9中的(椭)圆正反映了$\mathbf{k}\times(\mathbf{k}\times\mathbf{v})$、$\mathbf{k}\times\mathbf{v}$、$\mathbf{v}_{\perp}$三者“大小相等”的关系。最终，可知$\mathbf{v}_\perp=-\mathbf{k}\times(\mathbf{k}\times\mathbf{v})$。

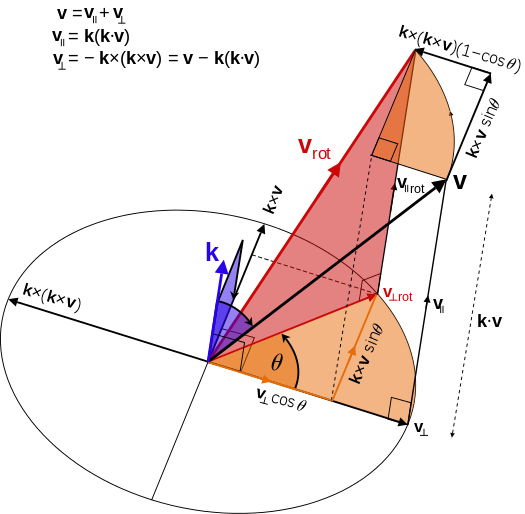
从图8还可以看出，v的平行分量$\mathbf{v}_\parallel$不会因为旋转而改变，旋转后的向量$\mathbf{v}_{rot}$ 的平行分量依然等于$\mathbf{v}_\parallel$，即$\mathbf{v}_{\parallel rot}=\mathbf{v}_\parallel$。

而v的正交分量$\mathbf{v}_\perp$ 在旋转过程中大小不变，方向会发生变化，即

\[ \begin{equation} \begin{split} &|\mathbf{v}_{\perp rot}|=|\mathbf{v}_\perp|\\ &\mathbf{v}_{\perp rot}=\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v}_\perp=\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v} \end{split} \end{equation} \]

式(12)中第2个等式通过图9可以得出，将圆看做$xOy$ 坐标系平面，$\mathbf{v}_\perp$所在的直线看做$x$ 轴，$\mathbf{k}\times\mathbf{v}$所在的直线看做$y$ 轴，结合三角函数，很容易用$\mathbf{v}_\perp$和$\mathbf{k}\times\mathbf{v}$表示出$\mathbf{v}_{\perp rot}$。

到这已经得出罗德里格斯公式了：

\[ \begin{equation} \begin{split} \mathbf{v}_{rot}&=\mathbf{v}_{\parallel rot}+\mathbf{v}_{\perp rot}\\ &=\mathbf{v}_\parallel+\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v}\\ &=\mathbf{v}_\parallel+\cos\theta(\mathbf{v}-\mathbf{v}_\parallel)+\sin\theta\mathbf{k}\times\mathbf{v}\\ &=\cos\theta\mathbf{v}+(1-\cos\theta)\mathbf{v}_\parallel+\sin\theta\mathbf{k}\times\mathbf{v}\\ &=\cos\theta\mathbf{v}+(1-\cos\theta)(\mathbf{k}\cdot\mathbf{v})\mathbf{k}+\sin\theta\mathbf{k}\times\mathbf{v} \end{split} \end{equation} \]

矩阵形式

在叉积部分提到过叉积可以表示为矩阵乘向量的形式，类似地，罗德里格斯旋转公式可以表示为旋转矩阵乘以向量的形式，$\mathbf{v}_{rot}=\mathbf{R}\mathbf{v}$，其中$\mathbf{R}$ 是旋转矩阵。在slam14讲中的表示如下：

\[ \begin{equation} \mathbf{R}=\cos\theta\mathbf{I}+(1-\cos\theta)\mathbf{k}\mathbf{k}^T+\sin\theta\mathbf{k}^\wedge \end{equation} \]

其中，$\mathbf{I}$表示单位矩阵，$\mathbf{k}$ 表示旋转向量，$\mathbf{k}^\wedge$表示由$\mathbf{k}$得到的反对称矩阵。从式(13)不难看出上式，另外，结合式(13)还可以得到下面这个式子：

\[ \begin{equation} \begin{split} \mathbf{v}_{rot}&=\mathbf{v}_{\parallel rot}+\mathbf{v}_{\perp rot}\\ &=\mathbf{v}_\parallel+\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v}\\ &=\mathbf{v}-\mathbf{v}_\perp+\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v}\\ &=\mathbf{v}+(\sin\theta)\mathbf{k}\times\mathbf{v}+(\cos\theta-1)\times\mathbf{v}_\perp\\ &=\mathbf{v}+(\sin\theta)\mathbf{k}\times\mathbf{v}+(1-\cos\theta)\mathbf{k}\times(\mathbf{k}\times\mathbf{v}) \end{split} \end{equation} \]

上式最后一个等号的推导用到了式(11)。从而，得出这个维基百科上的矩阵表示：

\[ \begin{equation} \begin{split} \mathbf{v}_{rot}=\mathbf{R}\mathbf{v}=\mathbf{v}+(\sin\theta)\mathbf{K}\mathbf{v}+(1-\cos\theta)\mathbf{K}^2\mathbf{v} \end{split} \end{equation} \]

其中，$\mathbf{R}=\mathbf{I}+(\sin\theta)\mathbf{K}+(1-\cos\theta)\mathbf{K}^2$，$\mathbf{K}$表示由旋转向量$\mathbf{k}$生成的反对称矩阵。

cv2.Rodrigues的注意事项

先看看OpenCV官方api文档对cv2.Rodrigues函数的说明：

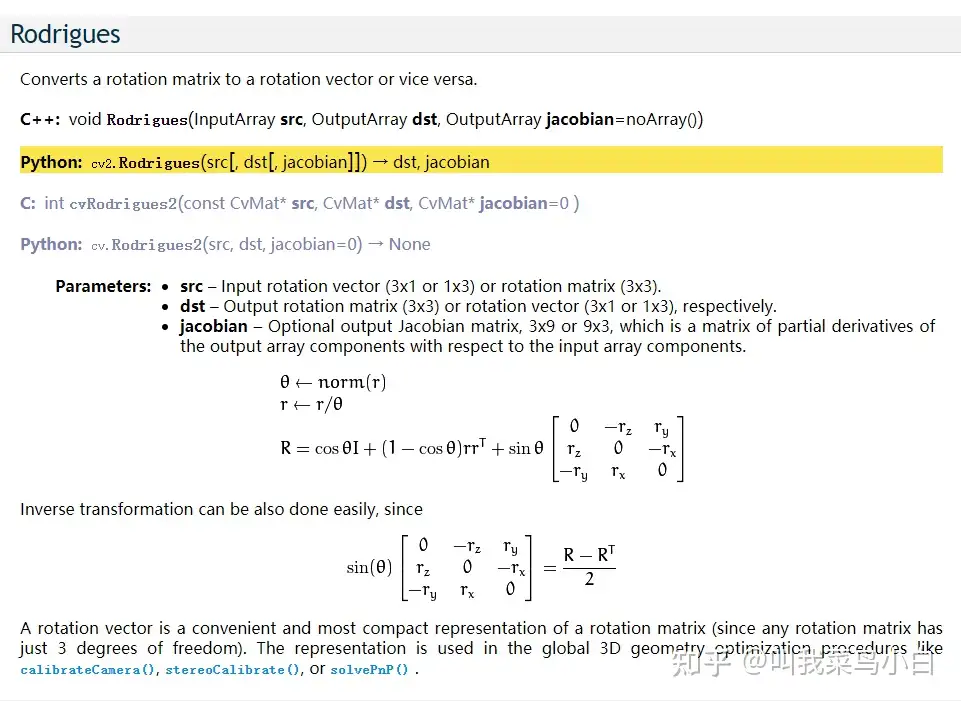
cv2.Rodrigues（）函数有两个功能：

1、输入旋转向量$r_{vec}$ 返回旋转矩阵R；

2、输入旋转矩阵R返回旋转向量$r_{vec}$和雅克比矩阵 $J$。

由公式（1）可知，由旋转角度 $\theta$ 和单位旋转轴向量$k$可以计算出旋转矩阵$R$。但是由OpenCV的官方文档可以看出，cv2.Rodrigues（）函数只有一个输入，即所谓的旋转向量 $r_{vec}$ 。其实所谓的旋转向量 $R = \theta k$ 。也就是说，再求旋转矩阵之前，你需要先计算旋转向量。

而在已知旋转矩阵R，使用cv2.Rodrigues（）函数欲求旋转轴k和旋转角度 $\theta$ 的时候，该函数返回一个元组。该元组第一项是3x1的旋转向量$r_{vec}$，第二项是9x3的雅克比矩阵 $J$。

若要获得旋转轴k和旋转角度 $\theta$，只需分别求$r_{vec}$的单位化和模长即可。

Preference

罗德里格斯旋转公式（Rodrigues' rotation formula）推导

罗德里格旋转公式及使用cv2.Rodrigues的注意事项