论文地址：

代码地址：

前言

一般来说，我们可以把姿态估计任务分成两个流派：Heatmap-based和Regression-based。

其主要区别在于监督信息的不同，Heatmap-based方法监督模型学习的是高斯概率分布图，即把GroundTruth中每个点渲染成一张高斯热图，最后网络输出为K张特征图对应K个关键点，然后通过argmax或soft-argmax来获取最大值点作为估计结果。这种方法由于需要渲染高斯热图，且由于热图中的最值点直接对应了结果，不可避免地需要维持一个相对高分辨率的热图（常见的是64x64，再小的话误差下界过大会造成严重的精度损失），因此也就自然而然导致了很大的计算量和内存开销。

Regression-based方法则非常简单粗暴，直接监督模型学习坐标值，计算坐标值的L1或L2 loss。由于不需要渲染高斯热图，也不需要维持高分辨率，网络输出的特征图可以很小（比如14x14甚至7x7），拿Resnet-50来举例的话，FLOPs是Heatmap-based方法的两万分之一，这对于计算力较弱的设备（比如手机）是相当友好的，在实际的项目中，也更多地是采用这种方法。

说到Regression-based方法的优点，可以简单总结为以下三点：

没有高分辨率热图，无负一身轻。计算成本和内存开销一起大幅降低。
输出为连续的，不用担心量化误差。（Heatmap-based输出的热图最大值点在哪，对应到原图的点也就确定了，输出热图的分辨率越小，这个点放大后对应回去就越不准。Regression-based输出为一个数值，小数点后可以有很多位，精度不受缩放影响）
可拓展性高。不论是one-stage还是two-stage，image-based还是video-based，2D还是3D，Regression-based方法都可以一把梭。此前就有用这种方法来将2D和3D数据放在一起联合训练的文章。这是Heatmap-based方法做不到的，因为输出是高度定制化的，2D输出必须渲染2D高斯热图，3D就必须渲染3D的高斯热图，计算量和内存开销也蹭蹭蹭地暴涨。
而Heatmap-based方法通过显式地渲染高斯热图，让模型学习输出的目标分布，也可以看成模型单纯地在学习一种滤波方式，将输入图片滤波成为最终希望得到的高斯热图即可，这极大地简化了模型的学习难度，且非常契合卷积网络的特性（卷积本身就可以看成一种滤波），并且这种方式规定了学习的分布，相对于除了结果以外内部一切都是黑盒的Regression-based方法，对于各种情况（遮挡、动态模糊、截断等）要鲁棒得多。基于以上种种优点，Heatmap-based方法在姿态估计领域是处于主导地位的，SOTA方案也都是基于此，这也导致了一种学术研究与算法落地的割裂，你在各种数据集和比赛里指标刷得飞起，但项目落地时我们工程师却只能干着急，因为你用的方法又慢又吃内存，真实项目里根本没法用啊。

终于，这一天有篇文章站出来说，重铸Regression荣光，吾辈义不容辞！不仅将Regression-based方法提到了超越Heatmap-based方法的高度，还保留了其一直以来的节省计算资源和内存资源的优点，真正做到了又快又准，简直是项目落地算法工程师的福音，接下来就让我们一起来学习一下这篇文章。

从极大似然估计（Maximum Likelihood Estimation, MLE）的角度来看问题，损失函数的选择其实是基于我们对目标分布的假设的，如果我们假设目标分布服从高斯分布，那么损失函数就应该选择L2 loss，如果假设为拉普拉斯分布，则应该选择L1 loss。

这里其实我还延申出来一个理解，早一些时候的文章大家都选择L2 loss作为损失函数，但近来越来越多的文章选择L1 loss，并且有详实的实验显示L1在大多数情况下都会优于L2，对于这个现象我一开始是作为一种实验得到的经验结论进行记忆的，但到这里我才理解，选择L2其实是一件很自然的事情，因为高斯分布具有大量优秀的特性：采样方便、解析的密度已知、KL距离容易计算，还有中心极限定理的保证——任何大的数据都趋近于高斯分布，所以你怎么用它几乎都是对的。但对于姿态估计任务而言，由于要精确地预测关键点位置，实际上概率分布是相对来说比较稀疏的，只有小部分区域具有概率，因此将拉普拉斯分布作为先验可能是一种更好的假设。

从这个视角来思考，我们其实可以把Heatmap-based方法看成是对模型的中间结果进行了监督，显式地要求模型学习高斯概率分布，进而得出结果；而Regression-based方法由于缺少对概率分布的监督约束，模型内部学到的分布是不稳定的，完全受到训练数据的支配，因此在性能和鲁棒性上逊于Heatmap-based方法也就不难想象了。

因此我们也可以知道，一个正确的密度函数假设对优化结果是起到主导性作用的。但在实际问题中，目标的分布是未知的，我们所掌握的数据也是有限的，模型很难单纯通过数据回归出真实的密度函数，有没有比草率地假设某一个分布更好的选择呢？有的，这里我们将引入这篇文章的核心之一，标准化流（Normalizing Flows）。

背景/动机

从高斯热图说起

众所周知，姿态估计分为坐标回归和热图回归两派，我一开始接触的就是热图回归。而热图回归中的热图一直以来都使用手工设计 $σ$ 的二维独立高斯分布。热图上某一位置 $x=(i,j)$ 的值则为

\[ \begin{equation}H(i,j)=e^{-\frac{(\mathbf{x}-\bm{\mu})^2}{2\sigma^2}}\end{equation} \]

其中 $\bm{\mu} = (\mathbf{\mu}_x, \mathbf{\mu}_y)$ 是该输入图片中该关键点的真实坐标点。那么为什么使用高斯分布呢？

坐标误差分布

便于理解，可以先从坐标回归的 $L_2$ 损失函数看起。坐标回归直接预测特征点坐标 $\bm{\hat\mu} $（有的也会同时预测 $\bm{\hat\sigma}$ ，代表误差分布的方差），而 $L_2$ 损失函数为：

\[ \begin{equation}L_{coord}=(\bm{\mu}-\bm{\hat{\mu}})2 \end{equation} \]

我们这边只先关注某一个关键点，如左肩膀。这个损失函数十分直观，即让预测的坐标点接近真实坐标点。它其实是由误差符合高斯分布的假设并经过极大似然估计而得。

极大似然估计

我们假设误差 $\bm{\epsilon}=\bm{\mu-\hat\mu}$ 符合期望为0、方差为 $\bm{\hat\sigma}$ 的高斯分布：

\[ \begin{equation}\Theta(\epsilon)=\frac{1}{\sqrt{2\pi}\hat\sigma}\exp({-\frac{\epsilon^2}{2\hat\sigma^2}})\end{equation} \]

这里预测了 $\hat\sigma$，代表对于不同人体特征点，误差分布的方差不同。

可以认为坐标回归预测了一个期望为 $\bm{\hat\mu}$ 、方差为 $\bm{\hat\sigma}$ 的高斯分布，即预测真实特征点的坐标在某一点 $\mathbf{x}$ 的概率满足该分布：

\[ \begin{equation}\Theta(\mathbf{x})=\frac{1}{\sqrt{2\pi}\bm{\hat\sigma}} e{-\frac{(\mathbf{x}-\bm{\hat\mu})2}{2\bm{\hat\sigma}^2}}\end{equation} \]

这一假设便是为什么热图回归中的热图采用高斯分布。而实际上我们观察到的样本为 $\mu$ ，那么采用极大似然估计法，我们就应该最大化 $p_\Theta(\mu)$ ：

\[ \begin{equation}L_{MLE}=-\rm{log}P_\Theta(\bm{\mu}) \propto \rm{log}\bm{\hat\sigma}+\frac{(\bm{\mu-\hat\mu})2}{2\bm{\hat\sigma}2}\end{equation} \]

如果我们假设 $\bm{\hat\sigma}$ 是常数，就可以从 5 式得到 2式。

如果使用拉普拉斯分布假设可以获得更好的性能，对应着 $L_1$ 损失函数。一个更接近真实误差分布的分布假设，应该能够有更好的性能，如下图所示。

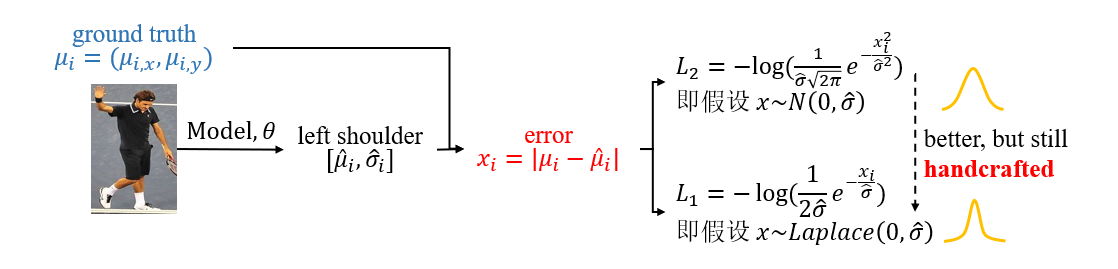
因此，更准确的概率密度函数可以带来更好的结果。然而，由于底层分布的解析表达式是未知的，该模型不能简单地回归几个值来构造密度函数，如公式5 来估计潜在分布并促进人体姿势回归，在下一节中，作者通过利用 normalized flow 来拟合更真实的分布得到一种更新颖的回归范例。

标准化流

标准化流是一类深度生成式模型，具体的数学原理有兴趣的朋友可以自行搜索，我这里比较肤浅地将其理解为，通过构造一个可逆的变换函数，能将一些基本的简单分布（如高斯分布）变换为任意的复杂分布。

这里用李宏毅老师的视频截图来进行直观展示，通过一系列可逆变换的叠加，可以将简单分布变换成任意的复杂分布：

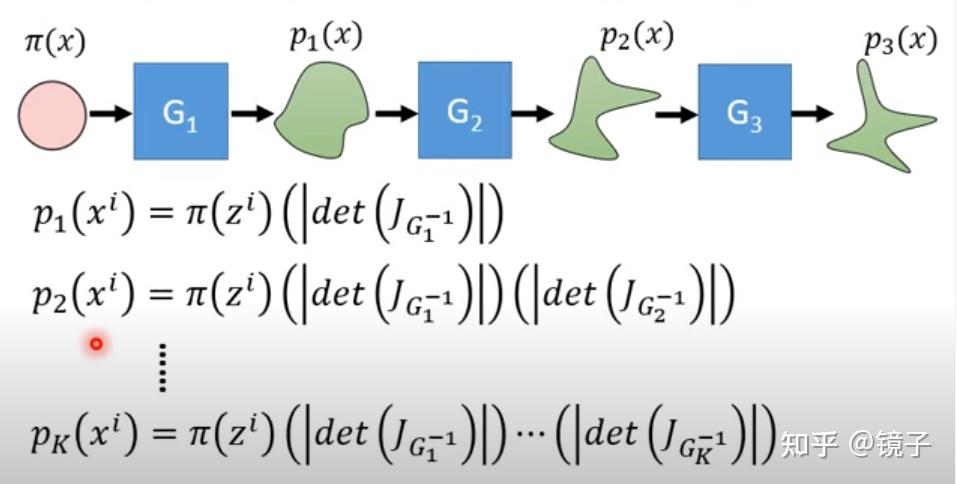
换句话说，虽然现阶段我们条件有限，我们的回归模型只能拟合一个简单分布，但我可以对拟合出来的结果进行变换，让变换后的结果更接近真实分布，只要我的变换足够复杂，理论上我可以拟合任意的目标分布。而这里的变换，实际上也就是我们的神经网络，因为神经网络理论上可以逼近任意的函数，因此流模型中那一系列叠加的可逆变换可以通过叠加的FC层实现。也就是说，我们将网络学习的目标，从让网络直接拟合目标分布，变成了拟合简单分布+流模型变换调整两个步骤。

具体关于flow的概念可以查看这里：

Designs

Basic Design

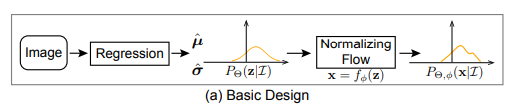
正则化流是一种通过可逆映射将简单分布转换成复杂分布的方法。它的核心思想是：

从一个简单的初始分布（如高斯分布）开始。
使用一个光滑且可逆的映射，将初始分布的随机变量 $z$ 映射到目标变量 $x$ 。
通过这种方式，构建能够拟合复杂分布的概率模型。
假设初始分布 $P_\Theta(z|I)$是一个随机变量 $ z$ 的概率密度函数，它由回归模型 $\Theta$ 的输出参数 $\bm{\hat\mu}$ 和 $\bm{\hat\sigma}$ 定义。并假设初始分布是高斯分布：

$$
P_\Theta(z|I) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(z-\mu)^2}{2\sigma^2}}

通过一个光滑且可逆的映射 $f_\phi$ ，将 $z$ 映射到 $x$ ：$x = f_\phi(z)$
其中：

$f_\phi$ 是由可学习参数 $\phi$ 定义的正则化流模型。
$f_\phi$ 的作用是将简单的初始分布 $P_\Theta(z|I)$ 转换为目标分布 $P_{\Theta,\phi}(x|I)$。
映射后的变量 $x$ 遵循新的分布 $P_{\Theta,\phi}(x|I)$。其概率密度函数可以通过以下公式计算：

\[ \log P_{\Theta,\phi}(x|I) = \log P_\Theta(z|I) + \log \left| \det \frac{\partial f_\phi^{-1}}{\partial x} \right| \]

其中：

$f_\phi^{-1}$ 是 $f_\phi$ 的逆映射，即 $z = f_\phi^{-1}(x)$ 。
$\det \frac{\partial f_\phi^{-1}}{\partial x}$ 是逆映射的雅可比行列式。
通过这个公式，可以从任意的 $ x$ 反向推导出 $z$，并估计对应的对数概率。

为了构造足够复杂的映射函数 $f_\phi$ ，可以将多个简单的映射按顺序组合起来：

\[ f_\phi(z) = f_K \circ \cdots \circ f_2 \circ f_1(z) \]

这意味着最终的映射是通过多个简单映射 $f_1, f_2, \cdots, f_K$ 的复合构成的。

为了训练模型，采用 最大似然估计（Maximum Likelihood Estimation, MLE）的方法。目标是最大化数据在模型分布下的对数概率。对数似然的损失函数定义为：

\[ \mathcal{L}_{\text{mle}} = -\log P_{\Theta,\phi}(x|I) \]

将映射函数 $ f_\phi $ 和初始分布 $P_\Theta(z|I)$代入后，损失函数可以写为：

\[ \begin{equation}\begin{aligned}\mathcal{L}_{\text{mle}} &= -\log P_{\Theta,\phi}(x|I)\Big|{x=\mu_g}\\ &= -\log P_\Theta(f_\phi^{-1}(\mu_g)|I) - \log \left| \det \frac{\partial f_\phi^{-1}}{\partial \mu_g} \right|\end{aligned}\end{equation} \]

其中 $ \mu_g$ 是目标位置。

需要注意的是，目标分布 $P_{\text{opt}}(x|I)$ 是未知的。正则化流模型通过最大化标注数据的对数似然来进行无监督学习。

对于某些具有挑战性的情况（如遮挡导致的标注误差较大），模型会自适应地预测一个具有较大方差的分布，以提高对数概率。

Reparameterization

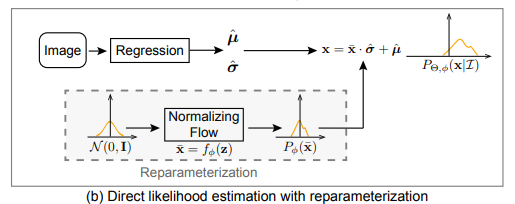
所以作者又提出了一种重参数化的方式来拟合最终概率密度函数:

假设所有潜在分布属于同一类概率密度函数（例如高斯分布），但均值和方差由输入$I$ 条件化。
通过重参数化，简化学习过程，使模型能够专注于学习分布的形状和偏差。
具体来说，首先正则化流模型 $f_\phi$ 被用来将零均值初始分布 $\tilde{z} \sim \mathcal{N}(0, \mathbf{I}) $ 映射为一个零均值的变形分布 $\tilde{x} \sim P_\phi(\tilde{x})$。

回归模型 $f_\Theta$ 输出两个值：

$\hat{\mu}$（均值）：用于控制分布的位置。
$\hat\sigma$（标准差）：用于控制分布的尺度。
最终分布 $ P_{\Theta,\phi}(x|I)$ 是通过对 $\tilde{x} $ 进行平移和缩放得到的：

\[ x = \tilde{x} \cdot \hat{\sigma} + \hat{\mu} \]

其中：

$\hat{\mu}$ 是回归模型预测的均值。
$\hat{\sigma} $ 是回归模型预测的标准差。
在引入重参数化后，最大似然估计的损失函数可以写为：

\[ \begin{equation}\begin{aligned}\mathcal{L}_{\text{mle}} &= -\log P_{\Theta,\phi}(x|I)\Big|{x=\mu_g}\\ & = -\log P_\phi(\tilde{\mu}_g) - \log \left| \det \frac{\partial \tilde{\mu}_g}{\partial \mu_g} \right| \\&= -\log P_\phi(\tilde{\mu}_g) + \log \hat{\sigma}\end{aligned}\end{equation} \]

其中，$\tilde{\mu}_g = (\mu_g - \hat{\mu}) / \hat{\sigma}$ 表示目标值 $\mu_g$ 与预测值 $\hat{\mu}$ 的偏差，经过标准化处理。故，$\frac{\partial \tilde{\mu}_g}{\partial \mu_g} = 1 / \hat{\sigma} $ 偏导数是标准差的倒数。

通过引入重参数化设计：

模型的学习重点转移到 $\tilde{\mu}_g$ 的分布上。
$\tilde{\mu}_g$ 反映了预测值与真实值之间的偏差。
这种设计能够更好地分离分布的形状（由 $f_\phi $ 学习）和位置/尺度（由 $\Theta$ 学习）。

RLE Loss

前言