深度相机
“工欲善其事必先利其器‘’我们先从能够获取RGBD数据的相机开始谈起。首先我们来看一看其分类。
根据其工作原理主要分为三类:
1.双目方案
基于双目立体视觉的深度相机类似人类的双眼,和基于TOF、结构光原理的深度相机不同,它不对外主动投射光源,完全依靠拍摄的两张图片(彩色RGB或者灰度图)来计算深度,因此有时候也被称为被动双目深度相机。比较知名的产品有STEROLABS 推出的 ZED 2K Stereo Camera和Point Grey 公司推出的 BumbleBee。
双目立体视觉是基于视差原理,由多幅图像获取物体三维几何信息的方法。在机器视觉系统中,双目视觉一般由双摄像机从不同角度同时获取周围景物的两幅数字图像,或有由单摄像机在不同时刻从不同角度获取周围景物的两幅数字图像,并基于视差原理即可恢复出物体三维几何信息,重建周围景物的三维形状与位置。
双目视觉有的时候我们也会把它称为体视,是人类利用双眼获取环境三维信息的主要途径。从目前来看,随着机器视觉理论的发展,双目立体视觉在机器视觉研究中发回来看了越来越重要的作用
为什么非得用双目相机才能得到深度?
说到这里,有些读者会问啦:为什么非得用双目相机才能得到深度?我闭上一只眼只用一只眼来观察,也能知道哪个物体离我近哪个离我远啊!是不是说明单目相机也可以获得深度?
在此解答一下:首先,确实人通过一只眼也可以获得一定的深度信息,不过这背后其实有一些容易忽略的因素在起作用:一是因为人本身对所处的世界是非常了解的(先验知识),因而对日常物品的大小是有一个基本预判的(从小到大多年的视觉训练),根据近大远小的常识确实可以推断出图像中什么离我们远什么离我们近;二是人在单眼观察物体的时候其实人眼是晃动的,相当于一个移动的单目相机,这类似于运动恢复结构(Structure from Motion, SfM)的原理,移动的单目相机通过比较多帧差异确实可以得到深度信息。
数学原理
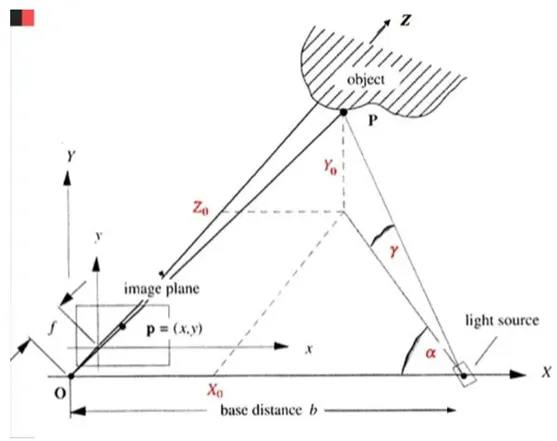
双目立体视觉是基于视差,由三角法原理进行三维信息的获取,即由两个摄像机的图像平面和物体之间构成一个三角形。已知两个摄像机之间的位置关系,便可以获得两摄像机公共视场内物体的三维尺寸及空间物体特征点的三维坐标。所以,双目视觉系统一般由两个摄像机构成。
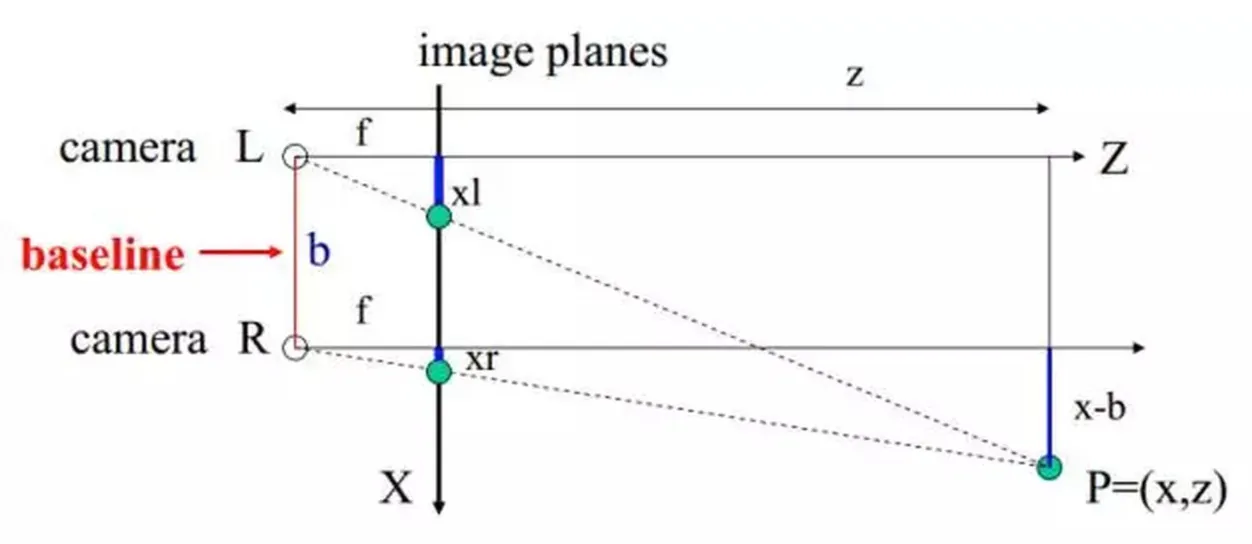
上图所示为简单的平视双目立体成像原理图,两摄像机的投影中心连线的距离,即基线距离\(b\) 。两摄像机在同一时刻观看时空物体的同一特征点P,分别在“左眼”和“右眼”上获取了点P的图像,他们的坐标分别为\(P_L=(X_L,Y_R)\);\(P_R=(X_R,Y_R)\)。将定两摄像机的图像在同一平面上,则特征点\(P\) 的图像坐标的Y坐标一定是相同的,即\(Y_L=Y_R=Y\)。由三角几何关系可以得到如下关系式:
则视差为:\(d=x_l-x_r\).由此可以计算出特征点P在摄像机坐标系下的三维坐标:
因此,左摄像机像面上的任意一点只要能在右摄像机像面上找到对应的匹配点,就完全可以确定该点的三维坐标。这种方法是点对点的运算,像平面上所有点只要存在相应的匹配点,就可以参与上述运算,从而获取对应的三维坐标。
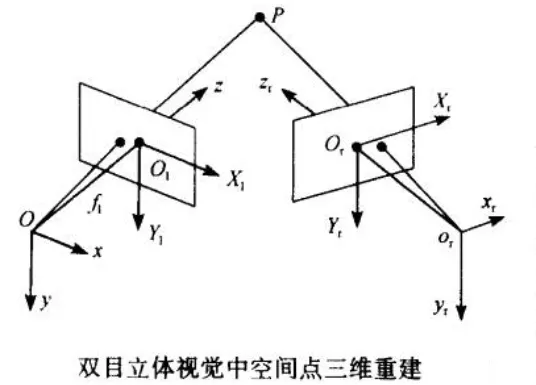
在分析了最简单的平视双目立体视觉的三维测量原理基础上,现在我们就有能力来考虑一般情况。如上图所示,设左摄像机\(O-xyz\)位于世界坐标系原点,且没有发生旋转,图像坐标系为\(O_l-X_1Y_1\),有效焦距为\(f_l\);右摄像机坐标系为\(O_r-xyz\),图像坐标系为\(O_r-X_rY_r\),有效焦距为\(f_r\)。那么根据摄像机的投射模型我们就能得到如下关系式:
因为\(O-xyz\)坐标系与\(O_r-x_ry_rz_r\)坐标系之间的位置关系可通过空间转换矩阵\(M_{lr}\)表示为:
同理,对于\(O-xyz\)坐标系中的空间点,两个摄像机面点之间的对应关系可以表示为
于是,空间点三维坐标可以表示为
因此,只要我们通过计算机标定技术获得左右计算机内参数/焦距\(f_r\),\(f_l\)和空间点在左右摄像机中的图像坐标,就能够重构出被测点的三维空间坐标。
2.结构光
结构光三维成像的硬件主要由相机和投射器组成,结构光就是通过投射器投射到被测物体表面的主动结构信息,如激光条纹、格雷码、正弦条纹等;然后,通过单个或多个相机拍摄被测表面即得结构光图像;最后,基于三角测量原理经过图像三维解析计算从而实现三维重建。例如Kinect v1和华硕xtion
结构光原理
基于结构光的三维成像,实际上是三维参数的测量与重现,主要是区别于纯粹的像双目立体视觉之类的被动三维测量技术,因而被称为主动三维测量。因为他需要主动去投射结构光到被测物体上,通过结构光的变形(或者飞行时间等)来确定被测物的尺寸参数,因此才叫做主动三维测量,嗯,相当主动。
首先,结构光的类型就分为很多种,既然是结构光,当然是将光结构化,简单的结构化包括点结构光,线结构光以及简单的面结构光等。复杂一点的结构化就上升到光学图案的编码了。结构光投射到待测物表面后被待测物的高度调制,被调制的结构光经摄像系统采集,传送至计算机内分析计算后可得出被测物的三维面形数据。其中调制方式可分为时间调制与空间调制两大类。时间调制方法中最常用的是飞行时间法,该方法记录了光脉冲在空间的飞行时间,通过飞行时间解算待测物的面形信息;空间调制方法为结构光场的相位、光强等性质被待测物的高度调制后都会产生变化,根据读取这些性质的变化就可得出待测物的面形信息。
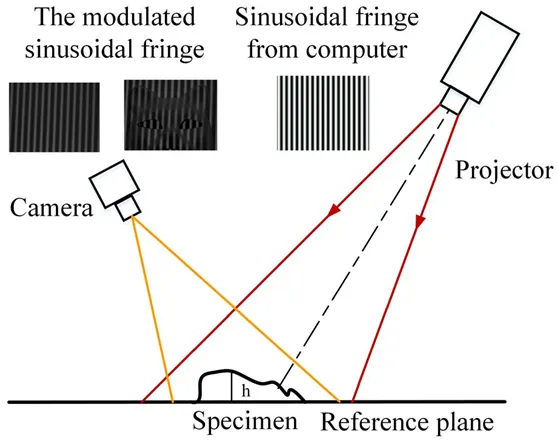
下面以一种应用广泛的光栅投影技术(条纹投影技术)为例来阐述其具体原理。条纹投影技术实际上属于广义上的面结构光。其主要原理如下图所示, 即通过计算机编程产生正弦条纹,将该正弦条纹通过投影设备投影至被测物,利用CCD相机拍摄条纹受物体调制的弯曲程度,解调该弯曲条纹得到相位,再将相位转化为全场的高度。当然其中至关重要的一点就是系统的标定,包括系统几何参数的标定和CCD相机以及投影设备的内部参数标定,否则很可能产生误差或者误差耦合。因为系统外部参数不标定则不可能由相位计算出正确的高度信息。
总体而言,结构光主要可以分为两类
- 线扫描结构光;
- 面阵结构光。
一般说结构光的时候都指代第二类,这里也主要关注面阵结构光。
线扫描结构光
线扫描结构光较之面阵结构光较为简单,精度也比较高,在工业中广泛用于物体体积测量、三维成像等领域。
数学基础
先来看一个简单的二维下的情况:
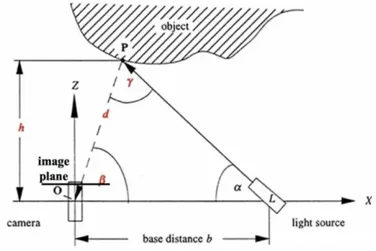
通过上图可以看到线扫描结构光装置的一个基本结构。主动光源\(L\)缓慢扫过待测物体,在此过程中,相机记录对应的扫描过程,最后,依据相机和光源在该过程中的相对位姿和相机内参等参数,就可以重建出待测物体的三维结构。
其中, \(α\) 为投影装置的朝向。 \(β\) 则需要通过对应像素的像素坐标 \(μ\)和焦距\(f\)来确定。最终可知\(P\)点的三维坐标为:\(P=(d\cdot cos\beta, d\cdot sin\beta)^T\), 将之推广至三维空间中:
可得
可以看到,三维空间中的情形和之前的二维空间类似,作为俯仰角的 \(γ\)并没有出现在公式中。
面阵结构光
面阵结构光大致可以分为两类:随机结构光和编码结构光。随机结构光较为简单,也更加常用。通过投影器向被测空间中投射亮度不均和随机分布的点状结构光,通过双目相机成像,所得的双目影像经过极线校正后再进行双目稠密匹配,即可重建出对应的深度图。如下图为某种面阵的红外结构光。

随机结构光这里就不再说了,因为和普通双目算法是很相似的。一些额外的考虑就是是否给相机加装滤光片、光斑的密度要到什么程度等硬件和光学的问题了。
这里主要讨论编码结构光。编码结构光可以分为两类:
- 时序编码;
- 空间编码。
时序编码
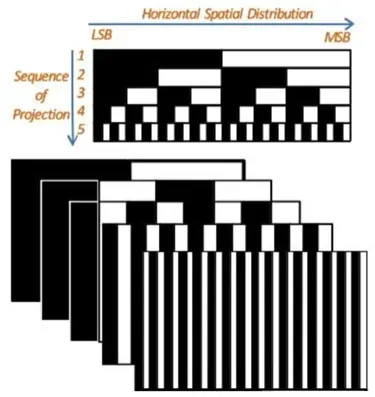
如上图,时序编码结构光即为在一定时间范围内,通过投影器向被测空间投射一系列明暗不同的结构光,每次投影都通过相机进行成像。假设共有n张影像,并设被阴影覆盖的部分编码值为1,未被覆盖的部分编码值为0。此时,每个像素都对应唯一一个长度为n的二进制编码,双目影像搜索匹配像素的问题就变成了查找具有相同编码值的像素。如果双目图像已经进行了极线校正,那么所投影的结构光只需要在x方向上不具有重复性即可。
优点:
- 高精度;
缺点:
- 只适用于静态场景;
- 需要拍摄大量影像。
空间编码
为满足动态场景的需要,可以采用空间编码结构光。前面谈到了随机结构光,就是不带编码信息,投影随机纹理,而这里讨论的空间编码结构光特指向被测空间中投影经过数学编码的、一定范围内的光斑不具备重复性的结构光。由此,某个点的编码值可以通过其临域获得。其中,包含一个完整的空间编码的像素数量(窗口大小)就决定了重建的精度。
3.TOF方案
TOF是Time of flight的简写,直译为飞行时间的意思。所谓飞行时间法3D成像,是通过给目标连续发送光脉冲,然后利用传感器接收从物体返回的光,通过探测光脉冲的飞行时间来得到目标物的距离。TOF的深度精度不随距离改变而变化,基本能稳定在cm级。
目前的消费级TOF深度相机主要有:微软的Kinect 2、 MESA 的 SR4000 、Google Project Tango 中使用的PMD Tech 的TOF深度相机等。这些产品已经在体感识别、手势识别、环境建模等方面取得了较多的应用,最典型的就是微软的Kinect 2。
TOF原理
飞行时间是从Time of Flight直译过来的,简称TOF。其基本原理是通过连续发射光脉冲(一般为不可见光)到被观测物体上,然后接收从物体反射回去的光脉冲,通过探测光脉冲的飞行(往返)时间来计算被测物体离相机的距离。
TOF法根据调制方法的不同,一般可以分为两种:脉冲调制(Pulsed Modulation)和连续波调制(Continuous Wave Modulation)。
脉冲调制
脉冲调制方案的原理比较简单,如下图所示。它直接根据脉冲发射和接收的时间差来测算距离。
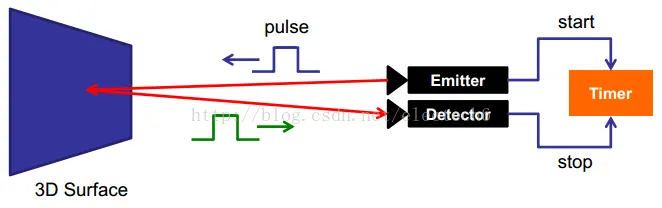
脉冲调制方案的照射光源一般采用方波脉冲调制,这是因为它用数字电路来实现相对容易。接收端的每个像素都是由一个感光单元(如光电二极管)组成,它可以将入射光转换为电流,感光单元连接着多个高频转换开关(下图的\(G0\),\(G1\))可以把电流导入不同的可以储存电荷(下图S0,S1)的电容里。
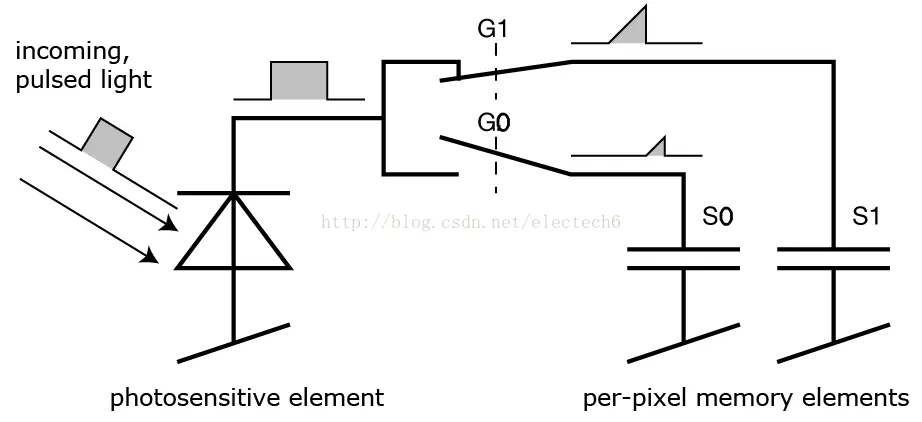
相机上的控制单元打开光源然后再关闭,发出一个光脉冲。在同一时刻,控制单元打开和关闭接收端的电子快门。接收端接收到的电荷\(S_0\)被存储在感光元件中。
然后,控制单元第二次打开并关闭光源。这次快门打开时间较晚,即在光源被关闭的时间点打开。新接收到的电荷\(S_1\)也被存储起来。具体过程如下图所示。
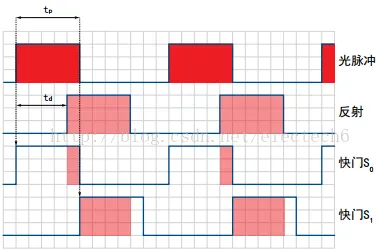
因为单个光脉冲的持续时间非常短,此过程会重复几千次,直到达到曝光时间。然后感光传感器中的值会被读出,实际距离可以根据这些值来计算。
记光的速度为\(c\),\(t_p\)为光脉冲的持续时间, \(S_0\)表示较早的快门收集的电荷, \(S_1\)表示延迟的快门收集的电荷,那么距离\(d\)可以由如下公式计算:
最小的可测量距离是:在较早的快门期间\(S_0\)中收集了所有的电荷,而在延迟的快门期间\(S_1\)没有收集到电荷,即\(S_1 = 0\)。代入公式会得出最小可测量距离\(d=0\)。
最大的可测量的距离是:在\(S_1\)中收集了所有电荷,而在\(S_0\)中根本没有收集到电荷。然后,该公式得出\(d= 0.5\times c\times t_p\)。因此最大可测量距离是通过光脉冲宽度来确定的。例如,\(t_p = 50 ns\),代入上式,得到最大测量距离\(d = 7.5m\)。
优点:
- 测量方法简单,响应较快
- 由于发射端能量较高,所以一定程度上降低了背景光的干扰
缺点: - 发射端需要产生高频高强度脉冲,对物理器件性能要求很高
- 对时间测量精度要求较高
- 环境散射光对测量结果有一定影响
连续波调制
实际应用中,通常采用的是正弦波调制。由于接收端和发射端正弦波的相位偏移和物体距离摄像头的距离成正比(见后面推导),因此可以利用相位偏移来测量距离。
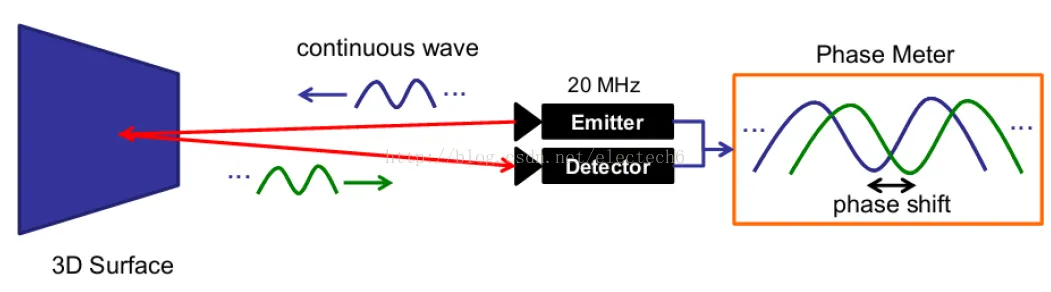
连续波调制的测量原理相对脉冲调制来说复杂一些,我们以最常用的连续正弦波调制来推导一下测量的原理。
连续正弦波调制测量方法,具体的推导过程如下。序号1-9对应下图的公式1-9。
- 假设发射的正弦信号\(s(t)\)振幅是\(a\),调制频率是\(f\)
- 经过时延 \(△t\)后接收到的信号为接收\(r(t)\),衰减后的振幅为\(A\),强度偏移(由环境光引起)为\(B\)
- 四个采样时间间隔相等,均为\(T/4\)
- 根据上述采样时间可以列出四个方程组
- 从而可以计算出发射和接收的正弦信号的相位偏移\(△φ\)
- 据此可以根据(6)中公式计算物体和深度相机的距离\(d\)
- 接收信号的衰减后的振幅\(A\)的计算结果
- 接收信号强度偏移B的计算结果,反映了环境光
- \(A, B\)的值间接的反应了深度的测量精度,深度测量方差可以用公式9近似表示。
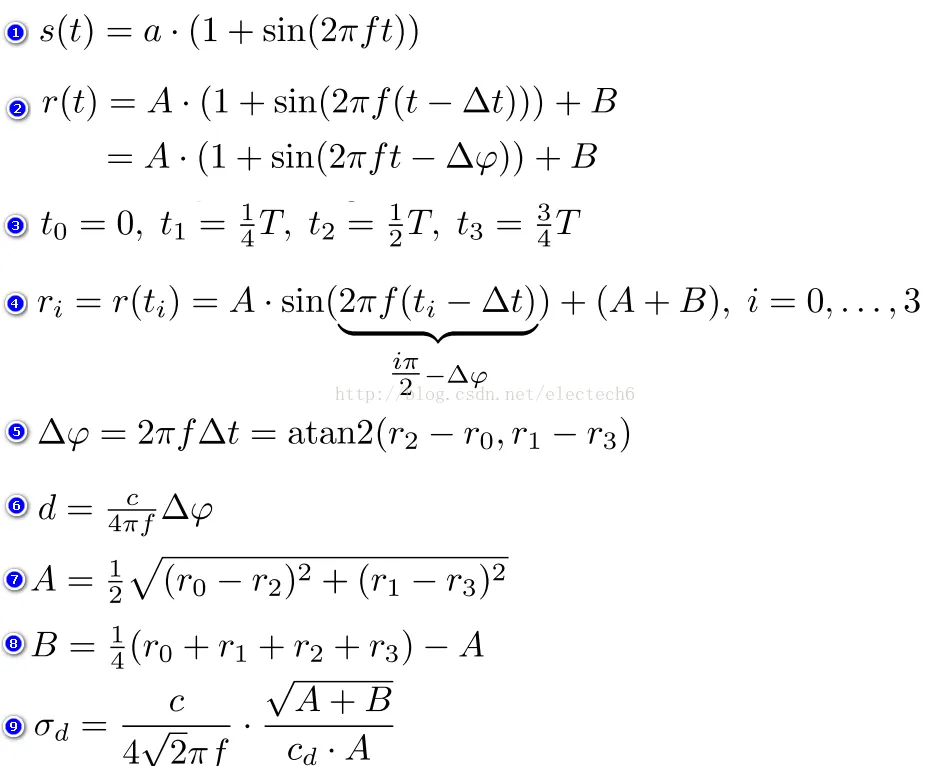
优点:
- 相位偏移(公式5)中的(\(r2-r0\))和(\(r1-r3\))相对于脉冲调试法消除了由于测量器件或者环境光引起的固定偏差。
- 可以根据接收信号的振幅A和强度偏移B来间接的估算深度测量结果的精确程度(方差)。
- 不要求光源必须是短时高强度脉冲,可以采用不同类型的光源,运用不同的调制方法
缺点: - 需要多次采样积分,测量时间较长,限制了相机的帧率
- 需要多次采样积分,测量运动物体时可能会产生运动模糊。
总结
TOF深度相机对时间测量的精度要求较高,即使采用最高精度的电子元器件,也很难达到毫米级的精度。因此,在近距离测量领域,尤其是1m范围内,TOF深度相机的精度与其他深度相机相比还具有较大的差距,这限制它在近距离高精度领域的应用。
但是,从前面的原理不难看出,TOF深度相机可以通过调节发射脉冲的频率改变相机测量距离;TOF深度相机与基于特征匹配原理的深度相机不同,其测量精度不会随着测量距离的增大而降低,其测量误差在整个测量范围内基本上是固定的;TOF深度相机抗干扰能力也较强。因此,在测量距离要求比较远的场合(如无人驾驶),TOF深度相机具有非常明显的优势。
关键技术参数:
1.检测范围;2.检测精度;3.检测角度;4.帧率;5.模块大小;6.功耗
目前的主流摄像头在检测范围、检测精度和检测角度等都相差不大,主要区别在于:
- 结构光方案优势在于技术成熟,深度图像分辨率可以做得比较高,但容易受光照影响,室外环境基本不能使用;
- TOF方案抗干扰性能好,视角更宽,不足是深度图像分辨率较低,做一些简单避障和视觉导航可以用,不适合高精度场合。受环境影响小,传感器芯片并不成熟,成本很高,实现量产困难。
- 双目方案,成本相对前面两种方案最低,但是深度信息依赖纯软件算法得出,此算法复杂度高,难度很大,处理芯片需要很高的计算性能,同时它也继承了普通RGB摄像头的缺点:在昏暗环境下以及特征不明显的情况下并不适用。
小结
- 双目方案:最大的问题在于实现算法需要很高的计算资源,导致实时性很差,而且基本跟分辨率,检测精度挂钩。也就是说,分辨率越高,要求精度越高,则计算越复杂,同时,纯双目方案受光照,物体纹理性质影响。
- 结构光方案:目的就是为了解决双目中匹配算法的复杂度和鲁棒性问题而提出,该方案解决了大多数环境下双目的上述问题。但是,在强光下,结构光核心技术激光散斑会被淹没。因此,不合适室外。同时,在长时间监控方面,激光发射设备容易坏,重新换设备后,需要重新标定
- TOF方案:传感器技术不是很成熟,因此,分辨率较低,成本高,但由于其原理与另外两种完全不同,实时性高,不需要额外增加计算资源,几乎无算法开发工作量,是未来。
相机标定
3D建模
3D Face model
人脸三维重建就是建立人脸的三维模型,它相对于二维人脸图像多了一个维度,在电影,游戏等领域应用广泛。目前获取人脸三维模型的方法主要包括三种,软件建模,仪器采集与基于图像的建模。
- 软件建模作为最早的三维建模手段,现在仍然是最广泛地在电影,动漫行业中应用。顶顶大名的3DMax就是典型代表
- 由于手工建模耗费大量的人力,三维成像仪器也得到了长期的研究和发展。基于结构光和激光仪器的三维成像仪是其中的典型代表,我们熟知的iphoneX中的人脸识别就是基于结构光进行三维人脸重建,正因如此才有iphonex中的三维人脸表情包。这些基于仪器采集的三维模型,精度可达毫米级,是物体的真实三维数据,也正好用来为基于图像的建模方法提供评价数据库。不过由于仪器的成本太高,一般的用户是用不上了。
- 基于图像的建模技术(image based modeling),顾名思义,是指通过若干幅二维图像,来恢复图像或场景的三维结构,这些年得到了广泛的研究。
基于人脸图像的三维重建方法非常多,常见的包括立体匹配,Structure From Motion(简称SfM),Shape from Shading(简称sfs),三维可变形人脸模型(3DMM)
深度估计
由RGB估计深度