给定一个包含$n$维数据$x$的数据集$D$, 简单起见，假设数据$x\in\{0,1\}$.

由于真正对联合分布建模的时候，$x，y$ 都是随机变量，故而只需讨论 $p(X)=p(x_1,...,x_n)$即可，毕竟只需要令$x_n=y$ 即可。

给定一个具体的任务，如MNIST中的手写数字二值图分类，从Generative的角度进行Represent，并在Inference中Learning.

下面先介绍：

描述如何对这个MINST任务建模 $p(X,Y)$（Representation）

对MNIST任务建模

对于一张pixel为 $28\times28$ 大小的图片，令 $x_1$ 表示第一个pixel的随机变量， $x_1\in\{0,1\}$，需明确：

任务目标：学习一个模型分布$p(x_1,...,x_{784}),x\in\{0,1\}$，使采样时 $x\sim p_\theta(X)$，$x$ 是一个logits数字的概率高
模型假设：
根据概率的链式法则，我们可以将 n 维上的联合分布分解为:

\[ p(\mathbf{x}) = \prod\limits_{i=1}^{n}p(x_i \vert x_1, x_2, \ldots, x_{i-1}) = \prod\limits_{i=1}^{n} p(x_i \vert \mathbf{x}_{< i } ) \]

链式法则可以用下图表示为贝叶斯网络

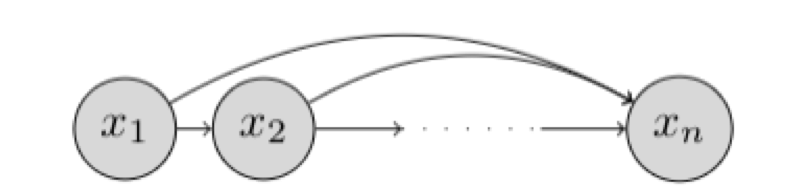
这种不做条件独立假设的贝叶斯网络被称为服从自回归性质。术语自回归源自关于时间序列模型的文献，其中使用来自先前时间步长的观测值来预测当前时间步长的值。在这里，我们固定变量$ x_1, x_2,..., x_n $ 的顺序，第 $i$ 个随机变量的分布取决于所选顺序中所有前面随机变量的值 $ x_1, x_2,..., x_{i-1}$.

如果我们允许以表格形式指定每个条件概率 $p (x_i | x _{<i})$，那么这样的表示是完全通用并且可以表示在 n 个随机变量上的任何可能分布。然而，这种表示的空间复杂度随着 $n$ 呈指数增长。

在自回归生成模型中，条件被指定为具有固定数量参数的参数化函数。也就是说，我们假设条件分布 $p (x_i | x_{ <i})$ 对应于伯努利随机变量，并学习将前面的随机变量 $x_1, x_2,..., x_{i − 1 }$映射到该分布的均值的函数。因此，我们有

\[ p_{\theta_i}(x_i \vert \mathbf{x}_{< i}) = \mathrm{Bern}(f_i(x_1, x_2, \ldots, x_{i-1})) \]

其中 $θ_i$ 表示用于指定均值函数的参数集 $f_i$：$\{0,1\}^{ i − 1} → [0,1]$。

自回归生成模型的参数数量由 $∑^n_{i = 1} | θ_i | $给出。正如我们将在下面的示例中看到的，参数的数量比之前考虑的表格设置少得多。然而，与表格设置不同，自回归生成模型不能表示所有可能的分布。它的表达能力受到以下事实的限制：我们将条件分布限制为伯努利随机变量，其均值通过参数化函数所指定。

在最简单的情况下，我们可以将函数指定为输入元素的线性组合，然后是 sigmoid 非线性输出。这为我们提供了fully-visible sigmoid belief network (FVSBN)的公式

\[ f_i(x_1, x_2, \ldots, x_{i-1}) =\sigma(\alpha^{(i)}_0 + \alpha^{(i)}_1 x_1 + \ldots + \alpha^{(i)}_{i-1} x_{i-1}) \]

其中， $\theta_i=\{\alpha^{(i)}_0,\alpha^{(i)}_1, \ldots, \alpha^{(i)}_{i-1}\}$代表mean function的参数，变量 $i$ 的条件需要 $i$ 个参数，因此模型中的参数总数为 $∑^n_{i=1}i=O(n^2)$ 。请注意，参数的数量远少于表格情况的指数复杂度。

提高自回归生成模型表达能力的一种自然方法是对均值函数使用更灵活的参数化表达，例如多层感知器 (MLP)。例如，考虑具有 1 个隐藏层的神经网络的情况。变量 $i $ 的均值函数可以表示为

\[ \mathbf{h}_i = \sigma(A_i \mathbf{x_{< i}} + \mathbf{c}_i)\\ \hat{x}_i=f_i(x_1, x_2, \ldots, x_{i-1}) =\sigma(\boldsymbol{\alpha}^{(i)}\mathbf{h}_i +b_i ) \]

其中， $\mathbf{h}_i \in \mathbb{R}^d$表示隐藏层，$\theta_i = \{A_i \in \mathbb{R}^{d\times (i-1)}, \mathbf{c}_i \in \mathbb{R}^d, \boldsymbol{\alpha}^{(i)}\in \mathbb{R}^d, b_i \in \mathbb{R}\}$为mean function的参数。该模型中的参数总数由矩阵 $A_i$ 主导， $O(n^2d)$。

Neural Autoregressive Density Estimator (NADE)提供了一种替代的基于 MLP 的参数化，它比普通方法在统计和计算上更有效。在 NADE 中，参数在用于评估条件的函数之间共享。特别地，隐藏层激活被指定为

\[ \mathbf{h}_i = \sigma(W_{., < i} \mathbf{x_{< i}} + \mathbf{c})\\ \hat{x}_i=f_i(x_1, x_2, \ldots, x_{i-1}) =\sigma(\boldsymbol{\alpha}^{(i)}\mathbf{h}_i +b_i ) \]

其中，$\theta=\{W\in \mathbb{R}^{d\times n}, \mathbf{c} \in \mathbb{R}^d, \{\boldsymbol{\alpha}^{(i)}\in \mathbb{R}^d\}^n_{i=1}, \{b_i \in \mathbb{R}\}^n_{i=1}\}$为均值函数 $f_1(\cdot), f_2(\cdot), \ldots, f_n(\cdot)$ 的完整参数集。权重矩阵 $W$ 和偏置向量 $c$ 在条件之间共享。

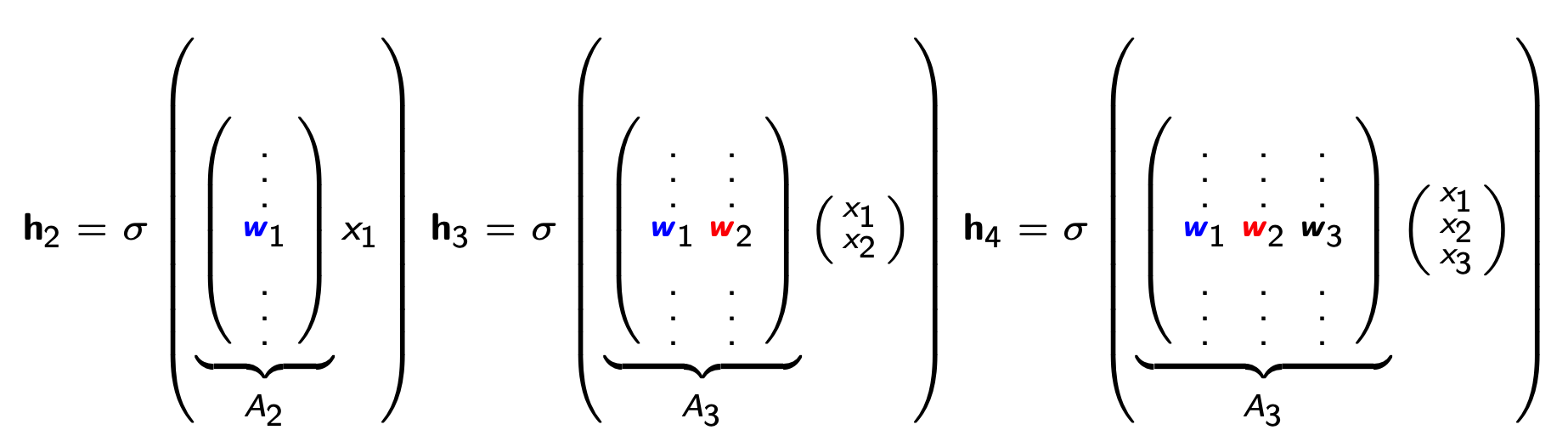
共享参数有两个好处：

参数总数从 $O(n^2d)$ 减少到 $O(nd)$
可以通过以下递归策略在 $O(nd)$ 时间内评估隐藏单元激活：

任务复杂度扩展RNADE（Random NADE）

上述NADE的任务背景是每个pixel均为二值变量 $x_i\in\{0,1\}$x, 现在先扩展到256个值的变量$x_i\in\{0,1,...,255\}$，再扩展到连续变量如 $x_i \sim N(u_i,\sigma_i)$.

多项式分布

先看看256个值的变量$x_i$，自然想到用多项式分布categorical distribution，即 $x_i\sim Cat(p_i^1,...,p_i^{256})$，对于第$i$个随机变量服从一个多项分布$Cat$，其参数为$p_i^k,k=1,...,256$

在NADE中有：

\[ \hat x_i=p(x_i|x_1,\dots,x_{i-1})=\sigma(\alpha_ih_i+b_i)\\ h_i=\sigma(Wx_{<i}+c_i)\\ \hat x_i=\sigma(\alpha_i\sigma(Wx_{<i}+c_i)+b_i) \]

因此RNADE有：

p(x_i|x_1,\dots,x_{i-1})=Cat(p_i^1,...,p_i^{256})\quad (1)\ \hat x_i=(p_i^1,...,p_i^{256})=softmax(X_ih_i+b_i)\quad (2)\ h_i=\sigma(Wx_{<i}+c_i)\quad (3)
$$

解释一下：
( 1 ) ：利用Autoregressive来建模联合分布，第$i$个随机变量的分布condition on前$i − 1$个随机变量的值，并服从一个多项式分布$C a t$（离散情况下的数量）
( 2 ) ：一个观测值$\hat{x} _ i$的多项式分布参数 $p_i^1,...,p_i^{256}$ 来自隐层输出$X_ih_i+b_i$的softmax
( 3 ) ：一个隐层的输入$h_i$ 与前面 $i-1$个随机变量有关

（最后想说的还是，该建模过程，通过假设分布，模型最后的输出拟合的是分布参数，采样观测值的分布，而并不是观测值本身）

高斯分布

连续变量的情况下，最容易想到的就是高斯分布了。根据上面的流程，看看建模过程是怎样的representation

\[ p(x_i|x_1,\dots,x_{i-1})=\sum_{j=1}^K\frac{1}{K}N(x_i;u_i^j,\sigma_i^j)\quad (1)\\ \hat x_i=(u_i^1...,u_i^K,\sigma_i^1,...,\sigma_i^K)=f(h_i)\quad (2)\\ h_i=\sigma(Wx_{<i}+c_i)\quad (3) \]

解释一下：
( 1 ) ：利用Autoregressive来建模联合分布，第 $i$ 个随机变量的分布condition on前 $i-1$个随机变量的值，并服从由K个高斯分布组成的混合高斯分布
( 2 ) ：一个观测值$\hat x_i$ 的混合高斯分布参数$(u_i^1...,u_i^K,\sigma_i^1,...,\sigma_i^K)$来自经过函数$f$映射的隐层输出$X_ih_i+b_i$

( 3 ) ：一个隐层的输入$ h_i$与前面 $i-1$个随机变量有关

以Autoregressive看Autoencoder与RNN

Autoregressive 的Autoencoder

上述提到的FVSBN、NADE、RNADE在建模联合分布时，都假设了第 $i$ 个随机变量的分布condition on前$i-1$个随机变量的值，并服从一个假设分布。
实际上自回归Autoregressive的意思，是指这堆随机变量之间组成一个DAG图，即随机变量之间存在条件独立性的约束，并不存在环。
我们看看Autoencoder的图，与RNADE想比，随机变量$x_1,x_2,x_3$之间并无条件独立性假设，而且值输入一次，1个pass，就可以得到三个观测值$ \hat x_1,\hat x_2,\hat x_3$，但是RNADE的 $n$ 个观测值 $\hat x_1,\hat x_2...\hat x_n$，需要值输入n次，n个pass，因为第 $i$ 个观测值取决于前 $i-1$ 个随机变量 $x_1,x_2,...,x_{i-1}$的值。

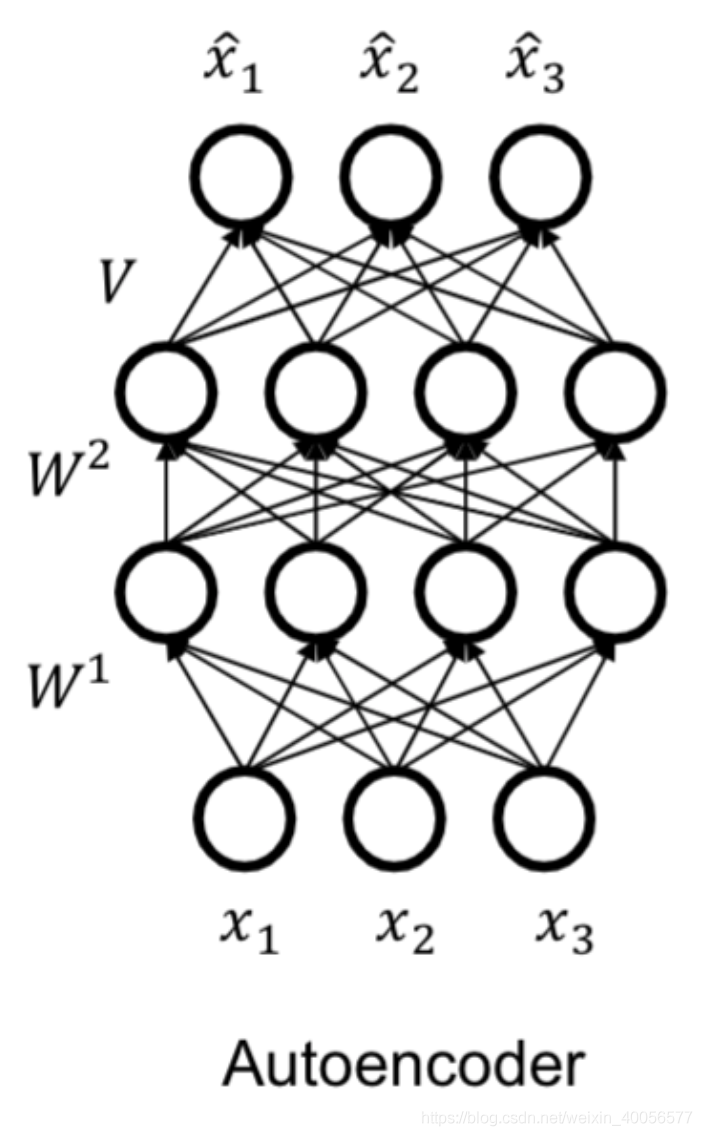
下面简要介绍一下Autoregressive的AutoEncoder，最主要的就是在随机变量之间施加条件独立性假设，具体做法就是通过Masks，如下图：

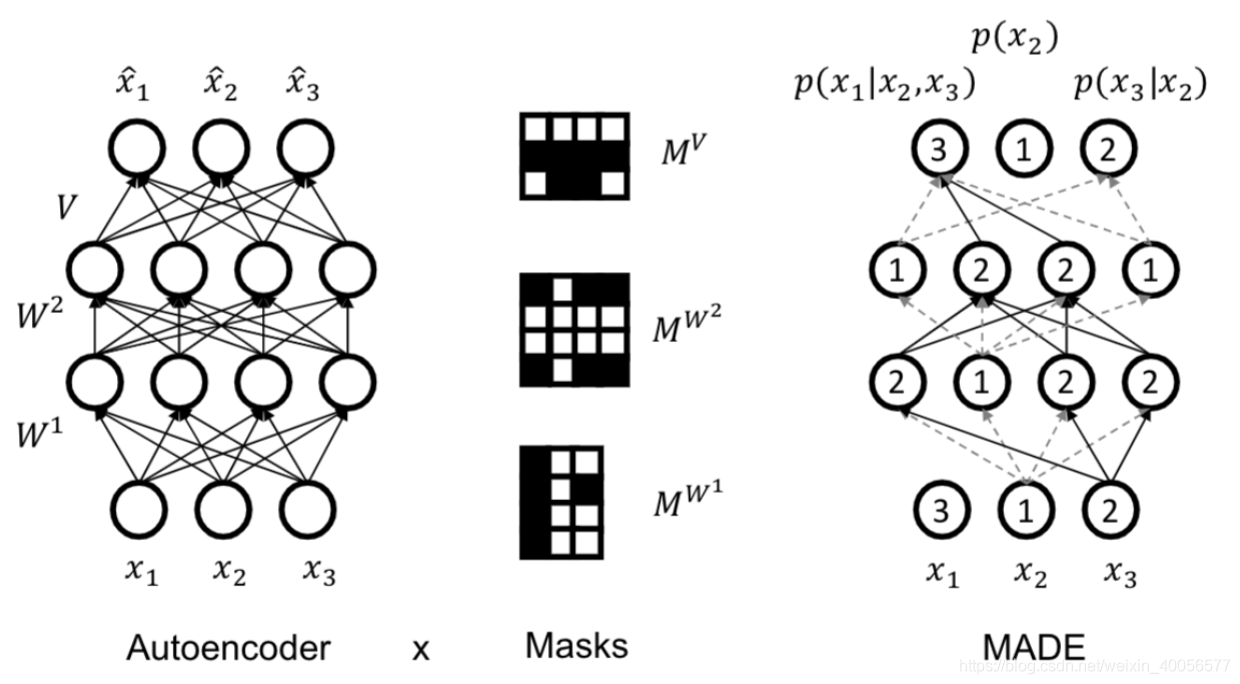
通过固定一个Mask来实现输入层随机变量与隐层之间的条件独立性假设，从而使得输出层的分布参数形成的分布如 $p(x_3|x_2)$ 带有了Autoregressive的特性。具体可参见这篇文章。
MADE: Masked Autoencoder for Distribution Estimation 2015 jmlr

带有Autoregressive特性的RNN

在上面的模型FVSBN,NADE,RNADE中，建模时有一个问题，即 $p(x_t|x_{1:t-1};\alpha^t)$ 随着变量个数或者序列长度t的增多，Hitory即 $x_{1:t-1}$ 一直在变长，造成计算量剧增。

Idea：解决这个histroy随序列变长的问题，就是从一开始就存储一个对History信息进行浓缩的Summary，并且每一次变长都更新这个Summary，就不需要每次都计算一遍历史信息了。

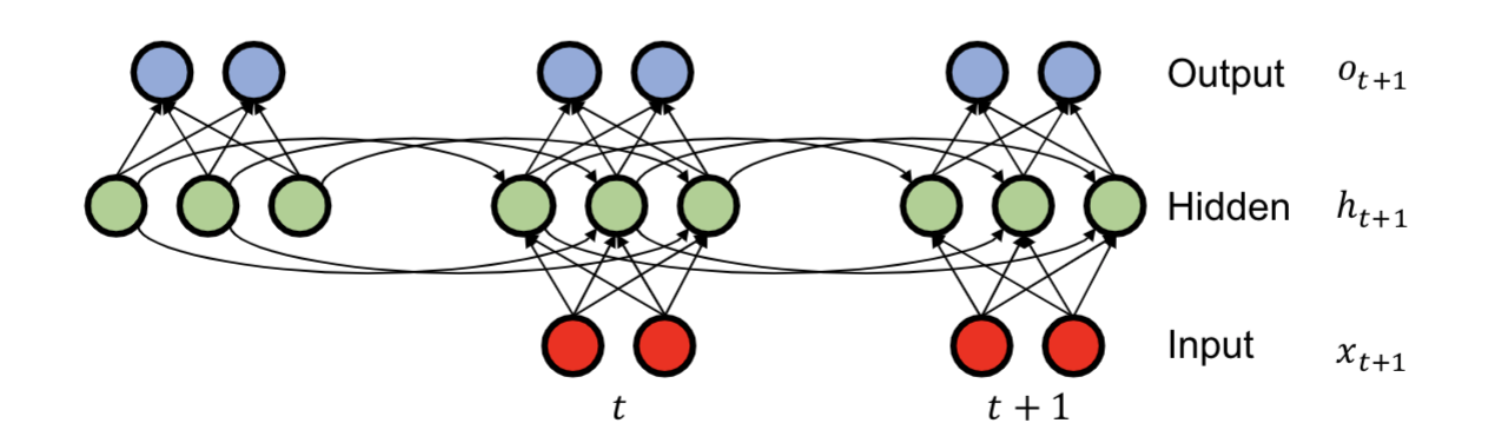
Summary update：$h_{t+1}=tanh(W_{hh}h_t+W_{xh}x_{t+1})$
Prediction：$o_{t+1}=W_{hy}h_{t+1}$
Summary Initalization：$h_0=b_0$
解释一下：
第t+1时刻的Summary = tanh(第t时刻的Summary+第t+1时刻的输入)
第t+1时刻的观测值observation = 第t+1时刻的Summary的变换
初始化Summary

一个为什么RNN自带Autoregressive的例子：

假设随机变量 $x_i\in\{h,e,l,o\}$, 使用one-hot编码
Autoregressive：

p(X)=p(X_1=h,X_2=e,X_3=l,X_4=l,X_5=o)=p(x_1=h)p(x_2=e|x_1=h)\dots p(X_5=o|X_1=h,X_2=e,X_3=l,X_4=l)
$$

当然除此以外，随机变量 $x_i$ 的取值可以是word，bi word，也是character，在图像中则为pixel，于是有Pixel RNN，Pixel CNN这样的模型，采用AutoRegressive建模的方式与上述差异不大。

Pixel RNN与Pixel CNN

主要对Image的pixel进行Autoregressive的角度，看看Pixel RNN与Pixel CNN的大致原理，顺便回顾下Autoregressive的Generative Model对一个问题的建模过程。

Pixel RNN

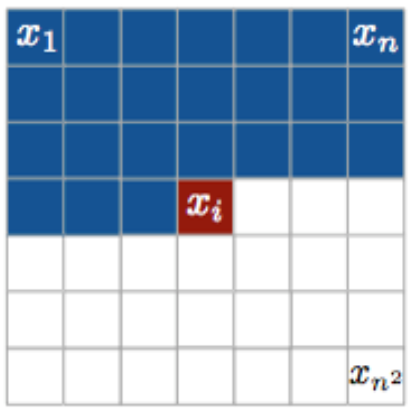
对于一张彩色的图片，假设随机变量条件独立性的顺序ordering，如 $x_1,x_2,...x_{n^2}$。Autoregressive总有一个ordering，毕竟是条件独立性

先研究变量 $x_i$ 的取值，因为是彩色图片，所以一个pixel的 $x_i$ 除了离散的256个灰度值，还有三个通道（R，G，B），所以 $x_i\in \{0,1,...,255,R,G,B\}$
联合分布有
对其建模
对于历史信息 $x_{1:t-1}$ 的处理采用RNN的形式，大致原理如下图所示

解释一下大意：

最底层的context即 $x_{1:t-1}$ 的历史信息值，作为conditon
中间层的R condition on $x_{1:t-1}$，即 $p(x_t^R|x_{1:t-1})$
中间层与顶层的G condition on $x_{1:t-1}，x_t^R$ 即 $p(x_t^G|x_{1:t-1},x_t^R)$
这三层的意思，是因为使用RNN来避免重复计算历史信息，即进行Summray的update。而Mask的作用在于，限制层间信息传输是服从条件独立性的，区别于Fully Connected。

Pixel CNN

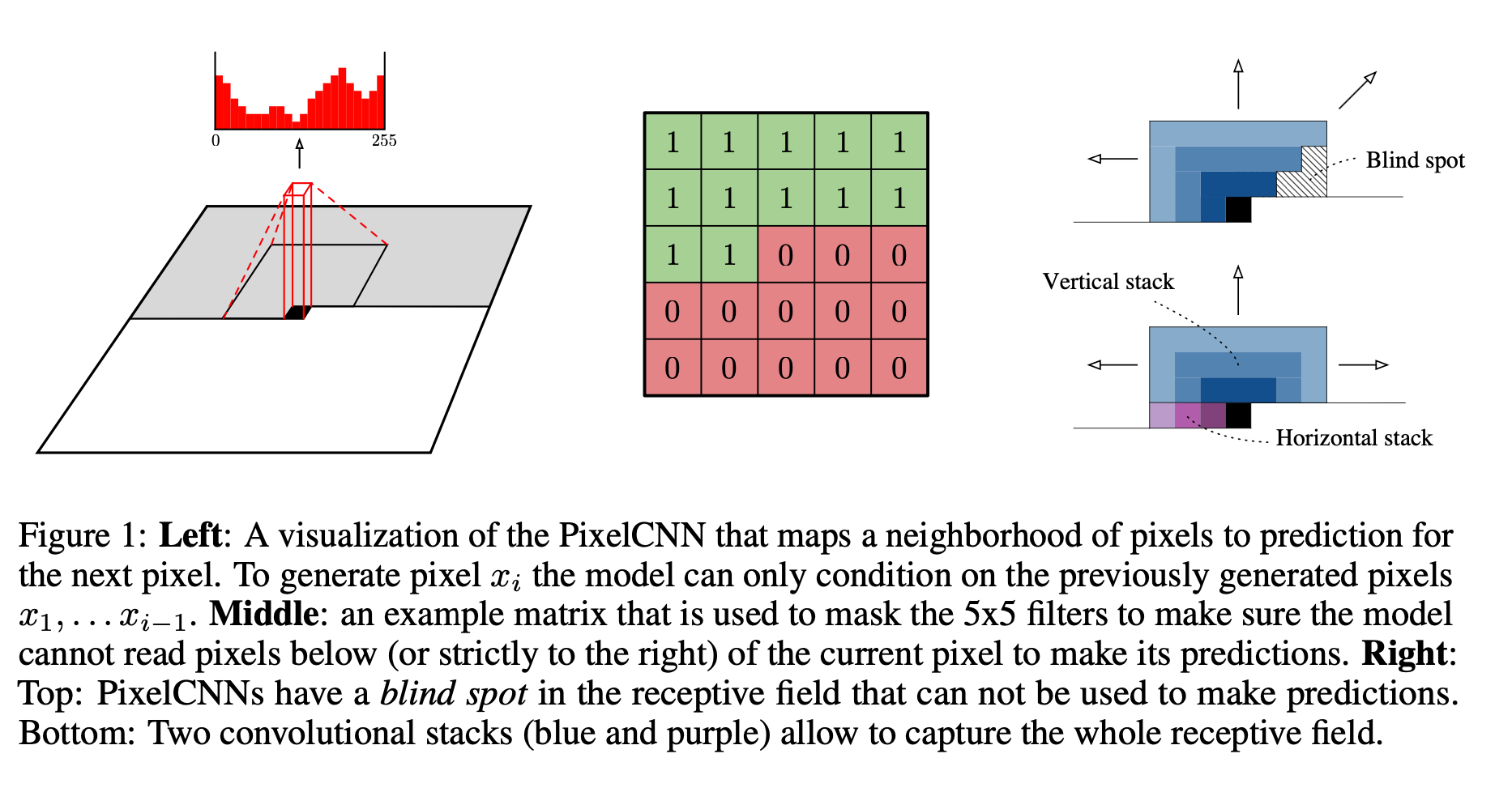
pytorch代码如下

class MaskedCNN(nn.Conv2d):
    """
    Implementation of Masked CNN Class as explained in A Oord et. al. 
    Taken from https://github.com/jzbontar/pixelcnn-pytorch
    """

    def __init__(self, mask_type, *args, **kwargs):
        self.mask_type = mask_type
        assert mask_type in ['A', 'B'], "Unknown Mask Type"
        super(MaskedCNN, self).__init__(*args, **kwargs)
        self.register_buffer('mask', self.weight.data.clone())

        _, depth, height, width = self.weight.size()
        self.mask.fill_(1)
        if mask_type =='A':
            self.mask[:,:,height//2,width//2:] = 0
            self.mask[:,:,height//2+1:,:] = 0
        else:
            self.mask[:,:,height//2,width//2+1:] = 0
            self.mask[:,:,height//2+1:,:] = 0


    def forward(self, x):
        self.weight.data*=self.mask
        return super(MaskedCNN, self).forward(x)

Pixel CNN与Pixel RNN的区别

Pixel RNN对联合分布的条件独立性假设是 $p(x_t|x_1,...,x_{t-1};\alpha^t)$；
Pixel CNN对联合分布的条件独立性假设是 $p(x_t|x_{neighborhood};\alpha^t)$
如上图所示，对第$i$ 个pixel的预测，condition on 邻居pixel时，是Pixel CNN；condition on 历史信息 $x_{1:i-1}$的pixels时，是Pixel RNN；
Pixel CNN与Pixel RNN比效果相当，但计算速度更快。
两者共同点
共同的地方就是把随机变量的取值 $\{0,1,...,255,R,G,B\}$分为 $\{0,1,...,255\}$与 $\{R,G,B\}$两个部分进行处理
对conditon on通道$\{R,G,B\}$的 $\{0,1,...,255\}$采用的都是多项式分布建模，对通道建模处理相同，即
实现条件独立性的顺序即condition on的做法，都是采用固定的mask进行，对于Pixel CNN选neighborhood的操作.

Autoregressive models 概述