1 BERT 方法回顾

在大规模预训练模型BERT 里面我们介绍了 BERT 的自监督预训练的方法，BERT 可以做的事情也就是Transformer 的 Encoder 可以做的事情，就是输入一排向量，输出另外一排向量，输入和输出的维度是一致的。那么不仅仅是一句话可以看做是一个sequence，一段语音也可以看做是一个sequence，甚至一个image也可以看做是一个sequence。所以BERT其实不仅可以用在NLP上，还可以用在CV里面。所以BERT其实输入的是一段文字，如下图1所示。

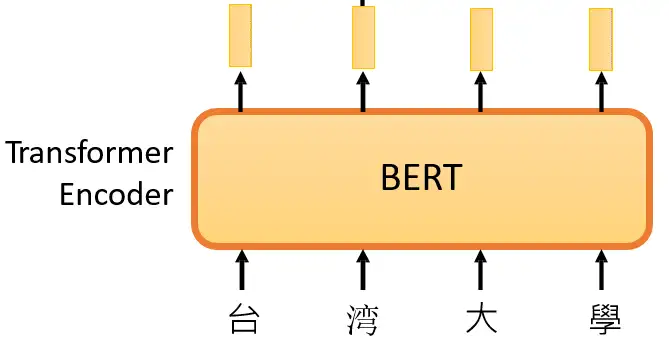
图1：BERT的架构就是Transformer 的 Encoder

接下来要做的事情是把这段输入文字里面的一部分随机盖住。随机盖住有 2 种，一种是直接用一个Mask 把要盖住的token (对中文来说就是一个字)给Mask掉，具体是换成一个特殊的字符。另一种做法是把这个token替换成一个随机的token。

图2：把这段输入文字里面的一部分随机盖住

接下来把这个盖住的token对应位置输出的向量做一个Linear Transformation，再做softmax输出一个分布，这个分布是每一个字的概率，如下图3所示。

那接下来要怎么训练BERT呢？因为这时候BERT并不知道被 Mask 住的字是 "湾" ，但是我们知道啊，所以损失就是让这个输出和被盖住的 "湾" 越接近越好，如下图4所示。

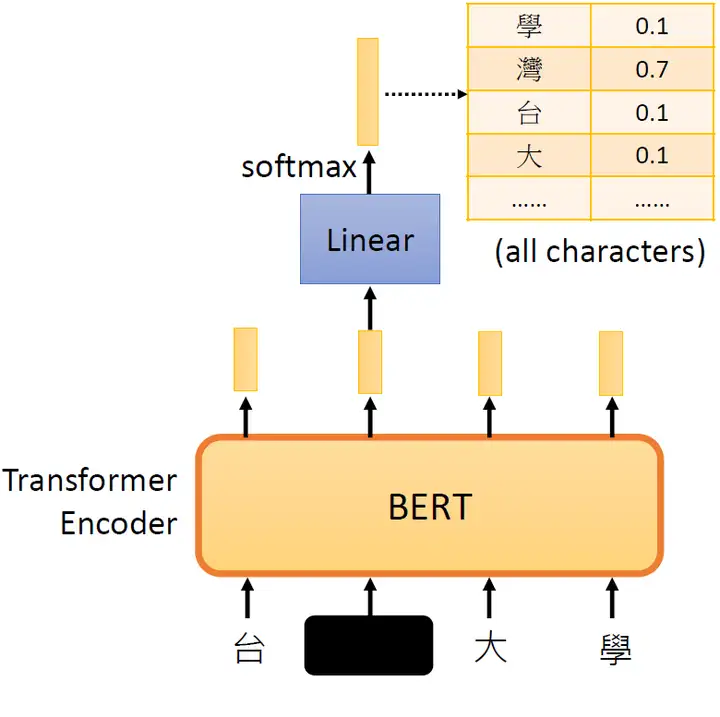
图3：把这个盖住的token对应位置输出的向量做一个Linear Transformation

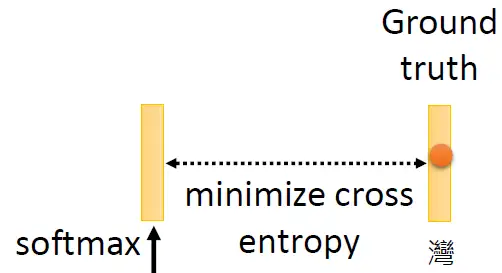
图4：让这个输出和被Mask 住的 token 越接近越好

其实BERT在训练的时候可以不止是选取一个token，我们可以选取一排的token都盖住，这就是 SpanBERT 的做法，至于要盖住多长的token呢？SpanBERT定了一个概率的分布，如图5所示。有0.22的概率只盖住一个token等等。

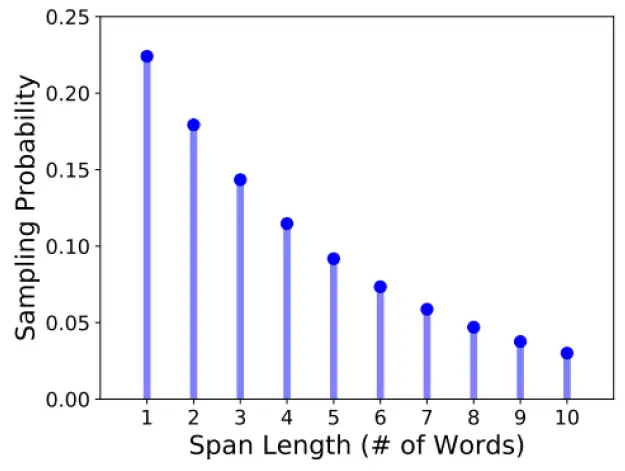
图5：SpanBERT定了一个概率的分布

除此之外，SpanBERT还提出了一种叫做Span Boundary Objective (SBO) 的训练方法，如下图6所示，意思是说：

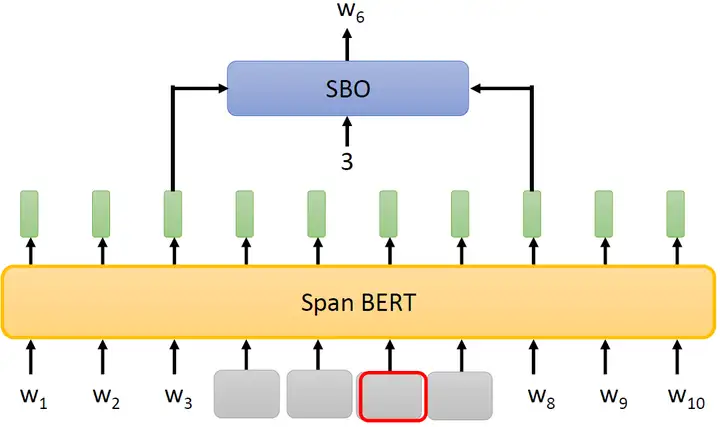
图6：Span Boundary Objective (SBO)

盖住一串token以后，用这段被盖住的token的左右2个Embedding去预测被盖住的token是什么。SBO把盖住的部分的左右两边的Embedding吃进来，同时还输入一个数字，比如说3，就代表我们要还原被盖住的这些token里面的第3个token。

就是通过上面的图1-图6的方法，让 BERT 看很多的句子，随机盖住一些 tokens，让模型预测盖住的tokens是什么，不断计算预测的 token 与真实的 token 之间的差异，利用它作为 loss 进行反向传播更新参数，来达到 Self-Supervised Learning 的效果。

Self-Supervised Learning 训练好 BERT 以后，如何在下游任务上使用呢？

我们就以情感分析为例，要求输入一个句子，输出对应的情感类别。

BERT是怎么解Sentiment Analysis的问题呢？给它一个句子，在这个句子前面放上 class token，这步和 ViT 是一模一样的。同样地，我们只取输出的Sequence里面的class token对应的那个vector，并将它做Linear Transformation+Softmax，得到类别class，就代表这个句子的预测的情感，如下图7所示。

值得注意的是，对于这种下游任务你需要有labelled data，也就是说 BERT 其实没办法凭空解Sentiment Analysis的问题，也是需要一部分有监督数据的。我们此时的情感分析模型包括：

BERT部分
Linear Transformation部分
只是BERT部分的初始化来自 Self-Supervised Learning，而 Linear Transformation 部分采样的是随机初始化。这两部分的参数都用Gradient Descent来更新。

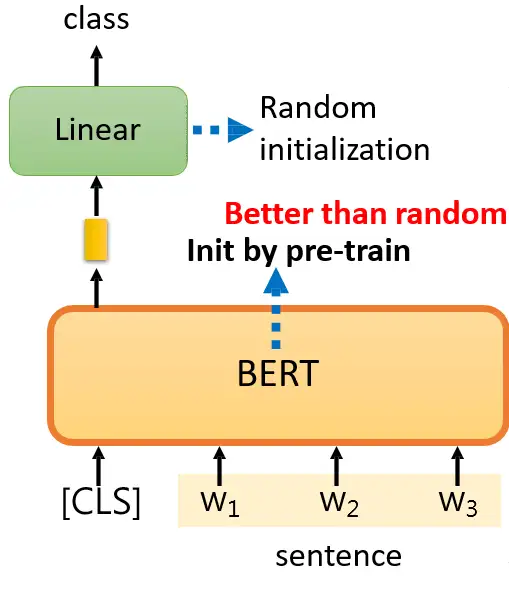
图7：使用BERT做情感分析

下图8其实是个对比，就是BERT部分不用预训练模型的初始化 (scratch) 和用了预训练模型的初始化 (fine-tune) 的不同结果，不同颜色的线代表GLUE中的不同任务。不用预训练模型的初始化会导致收敛很慢而且loss较高，说明预训练模型的初始化的作用。

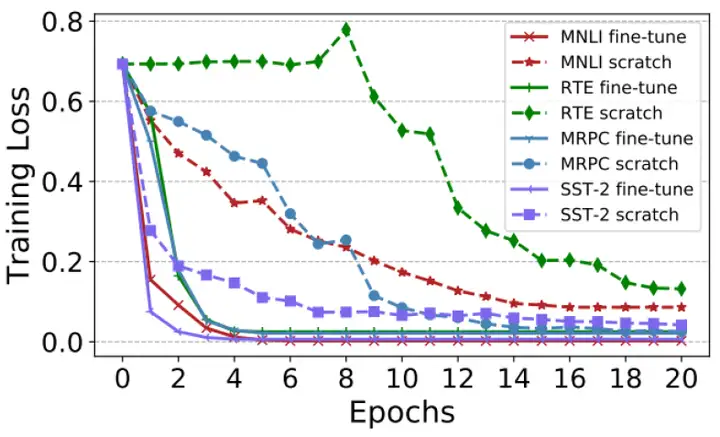
图8：预训练模型的初始化结果

2 BERT 可以直接用在视觉任务上吗？

上面的 BERT 都是在 NLP 任务上使用，因为 NLP 任务可以把每个词汇通过 Word2Vec 自动转化成一个固定大小的 token，我们随机盖住一些 token，让模型根据这个不完整的句子来预测被盖住的 token 是什么。那么一个自然而然的问题是：对于图片来讲，能否使用类似的操作呢？

第1个困难的地方是：视觉任务没有一个大的词汇表。在 NLP 任务中，比如图3所示，假设我们盖住词汇 "湾"，那么就想让模型根据这个不完整的句子来预测被盖住的 token 是 "湾"，此时我们有个词汇表，比如这个词汇表一共有8个词，"湾" 是第3个，则 "湾" 这个 token 的真值就是 GT=[0,0,1,0,0,0,0,0] ，只需要让模型的输出和这个 GT 越接近越好。

但是 CV 任务没有这个词汇表啊，假设我盖住一个 patch，让模型根据这个不完整的 image 来预测被盖住的 patch 是什么。那么对应的这个 GT 是什么呢？

BEIT 通过一种巧妙的方式解决了这个问题。

假设这个问题可以得到解决，我们就能够用 masked image modeling 的办法 (和BERT类似，盖住图片的一部分之后预测这部分) 训练一个针对图片的预训练模型，这个预训练模型就也可以像 BERT 一样用在其他各种 CV 的下游任务中啦。

3 BEIT 原理分析

论文名称：BEIT: BERT Pre-Training of Image Transformers

论文地址：

https://arxiv.org/pdf/2106.08254.pdfarxiv.org/pdf/2106.08254.pdf

本文提出的这个方法叫做 BEIT，很明显作者是想在 CV 领域做到和 NLP 领域的 BERT 一样的功能。在第1篇文章中提到，训练好的 BERT 模型相当于是一个 Transformer 的 Encoder，它能够把一个输入的 sentence 进行编码，得到一堆 tokens。比如输入 "台湾大学"，通过 BERT 以后会得到4个 tokens。并且这4个 tokens 也结合了sentence 的上下文。

那 BEIT 能不能做到类似的事情呢？，即能够把一个输入的 image 进行编码，得到一堆 vectors，并且这些个 vectors 也结合了 image 的上下文。

答案是肯定的。BEIT 的做法如下：

在 BEIT 眼里，图片有 2 种表示的形式：

image → image patches | visual tokens

在预训练的过程中，它们分别被作为模型的输入和输出，如下图9所示。

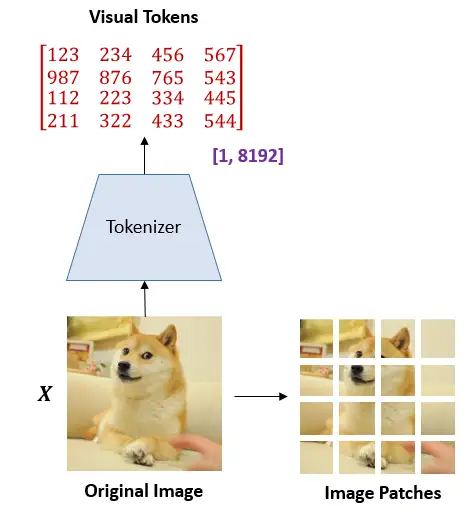
图9：图片有 2 种表示的形式：image patches or visual tokens

BEIT的结构可以看做2部分，分别是：

BEIT Encoder
dVAE
BEIT Encoder 类似于 Transformer Encoder，是对输入的 image patches 进行编码的过程，dVAE 类似于 VAE，也是对输入的 image patches 进行编码的过程，具体会在下面分别详细介绍。

3.1 将图片表示为 image patches

将图片表示为 image patches 这个操作和 Vision Transformer 对图片的处理手段是一致的。首先把 $x\in\mathcal{R^{H\times W\times C}}$ 的图像分成 $N=HW/P^2$ 个展平的2D块 $x^p\in\mathcal{R}^{N\times(P^2C)}$。

式中，$C$是 channel 数， $(W,H)$ 是输入的分辨率， $(P,P)$ 是块大小。每个 image patch 会被展平成向量并通过线性变换操作 (flattened into vectors and are linearly projected)。这样一来，image 变成了一系列的展平的2D块的序列，这个序列中一共有$N=HW/P^2$个展平的2D块，每个块的维度是$(P^2C)$。

实作时 P=16,H=W=224 ，和 ViT 一致。

问：image patch 是个扮演什么角色？

答：image patch 只是原始图片通过 Linear Transformation 的结果，所以只能保留图片的原始信息 (Preserve raw pixels)。

3.2 将图片表示为 visual tokens

这一步是啥意思呢？BEIT的一个通过 dVAE 里面一个叫做 image tokenizer 的东西，把一张图片$x\in\mathcal{R^{H\times W\times C}}$ 变成离散的 tokens $z=[z_1,...,z_N]\in \mathcal{V}^{h\times w}$ 。字典 $\mathcal{V}=\{1,...,|\mathcal{V}|\}$ 包含了所有离散 tokens 的索引 (indices)。

要彻底理解如何将图片表示为 visual tokens，那就得先从 VAE 开始讲起了，熟悉 VAE 的同学可以直接跳过3.2.1。

3.2.1 变分自编码器 VAE

VAE 跟 GAN 的目标基本是一致的——希望构建一个从隐变量 $Z$ 生成目标数据 $X$ 的模型，但是实现上有所不同。更准确地讲，它们是假设了$Z$ 服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型$X=g(Z)$，如下图10所示，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。

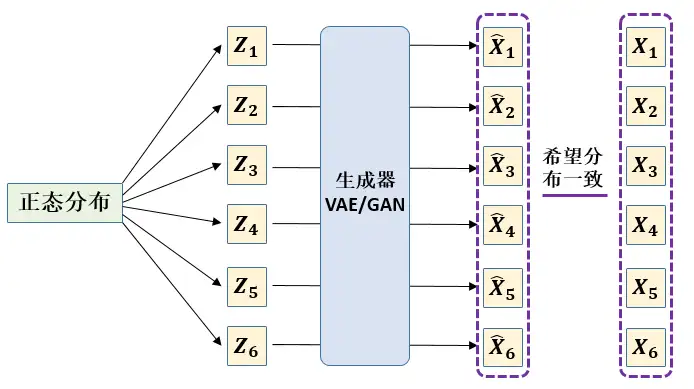
图10里面的 $Z$ 服从标准的正态分布，那么我就可以从中采样得到若干个$Z_{1},Z_{2},...,Z_{n}$，然后对它做变换得到 $\tilde{X_{1}}=g(Z_{1}),\tilde{X_{2}}=g(Z_{2}),...,\tilde{X_{n}}=g(Z_{n})$。注意这些 $\tilde{X_{i}}$ 都是通过 $g$ 重构出来的数据集，那如何衡量 $\tilde{X_{i}} $的分布与目标的数据集分布是不是一样的呢？注意在这里我们只有一堆重构出来的数据 $\tilde{X_{i}} $，但并不知道 $\tilde{X_{i}} (的分布是啥，所以没法用KL散度来衡量 (\tilde{X_{i}} \(的分布与目标的数据集分布的关系，因为KL散度是根据两个概率分布的表达式来算它们的相似度的。我们只有一批从构造的分布采样而来的数据$\left\{ \tilde X_{1},\tilde X_{2},...,\tilde X_{n} \right\}\)，还有一批从真实的分布采样而来的数据\)\left\{ X_{1},X_{2},...,X_{n} \right\}\)(也就是我们希望生成的训练集)。我们只有样本本身，没有分布表达式，当然也就没有方法算KL散度。

上面的假设是直接从正态分布中采样，实际情况是 $Z$ 由真实的分布采样而来的数据$\left\{ X_{1},X_{2},...,X_{n} \right\}$计算得到，并希望它接近标准正态分布。之后的步骤不变，假设$p(X|Z)$ 描述了一个由 Z 来生成 X 的模型，而我们假设 Z 服从标准正态分布，也就是$p(Z)\sim N(0,1)$。那么就可以按照图10的做法，从先从标准正态分布中采样一个$Z$，然后根据 $Z$ 来算一个 $X$。接下来就是结合自编码器来实现重构，保证有效信息没有丢失，再加上一系列的推导，最后把模型实现。框架的示意图如下图11所示。表达式为：

\[ p(X)=\sum_Zp(X|Z)p(Z) \]

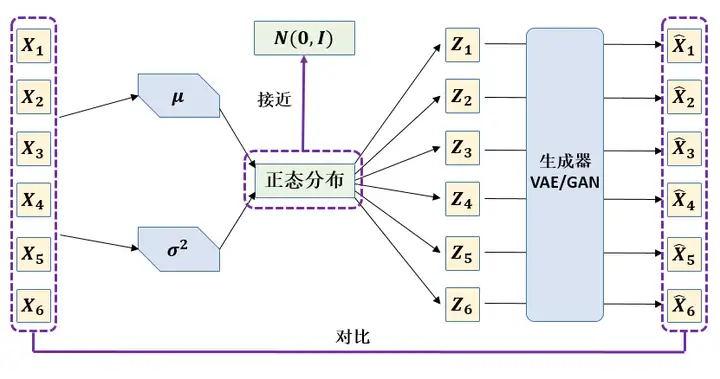
图11：VAE的传统理解

但如果像这个图的话，我们其实完全不清楚：究竟经过重新采样出来的$Z_k$，是不是还对应着原来的$X_k$。换句话说，采样得到的几个值和原来的几个样本的对应关系没有了。比如在图11里面， $Z_1$ 和 $X_1$ 是对应的吗，显然不是，因为 $Z_1$是从正态分布里面随机采样得到的。

所以我们如果直接最小化$D(\tilde X_{1},X_1)^2$(这里$D$代表某种距离函数)是很不科学的，而事实上你看代码也会发现根本不是这样实现的。

所以 VAE 到底是如何实现的呢？

在整个VAE模型中，我们并没有去使用 $p(Z)$(隐变量空间的分布)是正态分布的假设，我们用的是假设 $p(Z|X)$(后验分布)是正态分布，如下图12所示。

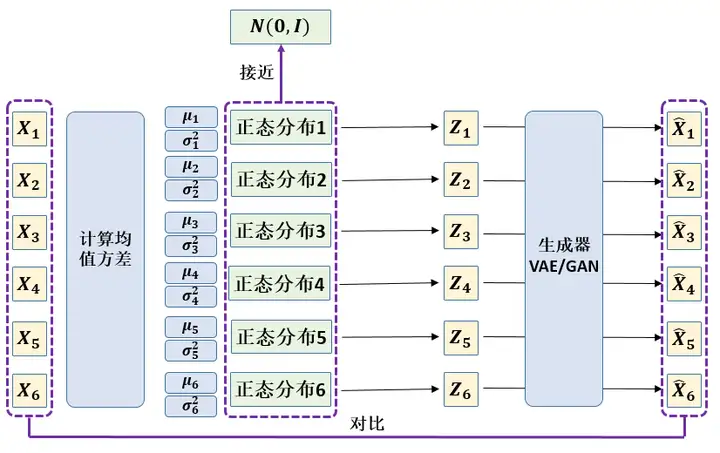
具体来说，给定一个真实样本$X_k$，我们假设存在一个专属于 $X_k$ 的分布 $p(Z|X_k)$，并进一步假设这个分布是（独立的、多元的）正态分布。为什么要强调“专属”呢？因为我们后面要训练一个生成器 $X=g(Z)$，希望能够把从分布 $p(Z|X_k)$采样出来的一个$Z_k$ 还原为 $X_k$。如果假设 $p(Z)$ 是正态分布，然后从 $P(Z)$中采样一个$Z$，那么我们怎么知道这个 $Z$ 对应于哪个真实的 $X$ 呢？现在 $p(Z|X_k)$专属于$X_k$，我们有理由说从这个分布采样出来的 $Z$ 应该要还原到 $X_k$ 中去。

这时候每一个$X_k$都配上了一个专属的正态分布，才方便后面的生成器做还原。但这样有多少个$X$ 就有多少个正态分布了。我们知道正态分布有两组参数：均值 $\mu$ 和方差 $\sigma^2$（多元的话，它们都是向量），那我怎么找出专属于$X_k$ 的正态分布 $p(Z|X_k)$的均值和方差呢？就是通过一个神经网络来拟合出来。我们构建两个神经网络$\mu_k=f_1(X_k)$，$log\sigma^2_k=f_2(X_k)$来算它们了。我们选择拟合 $log\sigma_k^2$而不是直接拟合$\sigma^2_k$，是因为 $\sigma^2_k$ 总是非负的，需要加激活函数处理，而拟合 $log\sigma^2_k$ 不需要加激活函数，因为它可正可负。到这里，我能知道专属于$X_k$的均值和方差了，也就知道它的正态分布长什么样了，然后从这个专属分布中采样一个$Z_k$出来，然后经过一个生成器得到$\tilde{X}_k=g(Z_k)$，现在我们可以放心地最小化 $D(\tilde{X}_k, X_k)^2$，因为 $Z_k$ 是从专属 $X_k$ 的分布中采样出来的，这个生成器应该要把开始的$X_k$还原回来。

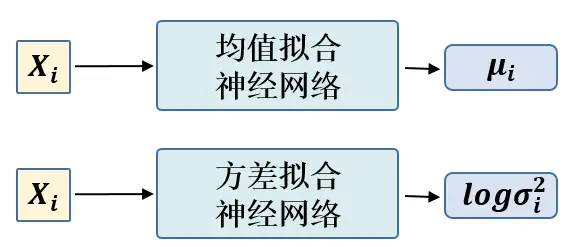
为什么要让均值方差拟合网络的输出分布 $p(Z|X)$ 接近标准正态分布 $N(0, 1)$ 呢？

如果没有这个约束的话，最终会得到什么结果呢？目标函数是最小化$D(\tilde{X}_k, X_k)^2$，这个重构过程受到噪声的影响，因为 $Z_k$ 是通过重新采样过的，不是直接由encoder算出来的。显然噪声会增加重构的难度，不过好在这个噪声强度（也就是方差）通过一个神经网络算出来的，所以最终模型为了重构得更好，肯定会想尽办法让方差为0。而方差为0的话，也就没有随机性了，生成的数据的范围就只在 $\{X_1, X_2, ..., X_n\}$ 里面了，模型会慢慢退化成普通的AutoEncoder，所以不管怎么采样其实都只是得到确定的结果（也就是均值），只拟合一个当然比拟合多个要容易，而均值是通过另外一个神经网络算出来的。

说白了，模型会慢慢退化成普通的AutoEncoder，噪声不再起作用。

所以，VAE 这里还让所有的 $p(Z|X)$，即均值方差拟合网络的输出分布接近标准正态分布 $N(0, 1)$，这样就防止了噪声为零，同时保证了模型具有生成能力。怎么理解“保证了生成能力”呢？如果所有的 $p(Z|X)$都很接近标准正态分布 $N(0, 1)$，那么根据定义：

\[ p(Z)=\sum_Xp(Z|X)p(X)=\sum_XN(0, 1)p(X)=N(0, 1) \]

这样我们就能达到我们的先验假设： $p(Z)$是标准正态分布，也就克服了退化成普通的AutoEncoder的问题。

那怎么均值方差拟合网络的输出分布$p(Z|X)$接近标准正态分布 $N(0, 1)$ 呢？

如果没有外部知识的话，其实最直接的方法应该是在重构误差的基础上中加入额外的loss：

\[ L_\mu=||f_1(X_k)||^2\\ L_{\sigma^2}=||f_2(X_k)||^2 \]

因为它们分别代表了均值 $\mu_k$ 和方差的对数 $log\sigma^2_k$ ，达到 $N(0, 1)$ 就是希望二者尽量接近于0了。不过，这又会面临着这两个损失的比例要怎么选取的问题，选取得不好，生成的图像会比较模糊。所以，原论文直接算了一般（各分量独立的) 正态分布与标准正态分布的KL散度 $KL(N(\mu, \sigma^2)||N(0, 1))$ 作为这个额外的loss：

一元正态分布的情形即可，根据定义我们可以写出

\[ \begin{aligned} KL(N(\mu, \sigma^2)||N(0, 1))&=\int_{}^{}\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-(x-\mu)^{2}/2\sigma^{2}}(log \frac{e^{-(x-\mu)^2/2\sigma^2}/\sqrt{2\pi\sigma^2}}{e^{-(x)^2/2}/\sqrt{2\pi}})dx\\ &=\int_{}^{}\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-(x-\mu)^{2}/2\sigma^{2}}(log\left\{ \frac{1}{\sqrt{\sigma^{2}}}exp\left\{ \frac{1}{2}[x^{2}-(x-\mu)^{2}/\sigma^{2}] \right\} \right\})dx\\ &=\frac{1}{2}\int_{}^{}\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-(x-\mu)^{2}/2\sigma^{2}}[-log\sigma^{2}+x^{2}-(x-\mu)^{2}/\sigma^{2}]dx\\ &=\frac{1}{2}({-log\sigma^{2}+\mu^{2}+\sigma^{2}-1}) \end{aligned} \]

整个结果分为三项积分，第一项实际上就是$-log\sigma^{2}$乘以概率密度的积分（也就是1），所以结果是$-log\sigma^{2}$；第二项实际是正态分布的二阶矩，熟悉正态分布的朋友应该都清楚正态分布的二阶矩为$\mu^{2}+\sigma^{2}$；而根据定义，第三项实际上就是“-方差除以方差=-1”。所以总结果就是上面的最后一行。

所以正态分布与标准正态分布的KL散度 $KL(N(μ,σ^{2})||N(0,1))$ 这个额外的loss计算结果为：

\[ L_{\mu,\sigma^{2}}=\frac{1}{2}\sum_{i=1}^{d}{\mu_{i}^{2}+\sigma_{i}^{2}-log\sigma_{i}^{2}-1} \]

这里的 d 是隐变量 Z 的维度，而 $\mu_{i}$ 和 $\sigma_{i}$ 分别代表一般正态分布的均值向量和方差向量的第 i 个分量。直接用这个式子做补充loss，就不用考虑均值损失和方差损失的相对比例问题了。显然，这个loss也可以分两部分理解：

\[ \begin{align} &L_{\mu,\sigma^{2}}=L_{\mu}+L_{\sigma^{2}}\\ &L_{\mu}=\frac{1}{2}\sum_{i=1}^{d}{\mu_{i}^{2}}=\frac{1}{2}||f_{1}(X)||^{2}\\ &L_{\sigma^{2}}=\frac{1}{2}\sum_{i=1}^{d}{(\sigma_{i}^{2}-log\sigma_{i}^{2}-1)} \end{align} \]

所以 VAE 模型的总的损失函数为：

\[ L=E_{x\sim \tilde p(x)}[E_{z\sim \tilde p(z|x)}[\color{purple}{-logq(x|z)}+\color{crimson}{KL(p(z|x)||q(z))}]] \]