Diffusion Models from SDE

连续扩散模型 (Continuous Diffusion Models) 将传统的离散时间扩散过程扩展到连续时间域,可以被视为一个随机过程，使用随机微分方程(SDE)来描述。其前向过程可以写成如下形式：

\[ \begin{equation}\mathrm d\mathbf x=\mathbf f(\mathbf x,t)\mathrm dt+g(t)\mathrm d\mathbf w\end{equation} \]

其中，$f(x,t)$ 可以看成偏移系数，$g(t)$ 可以看成是扩散系数，$dw$ 是标准布朗运动。这个SDE
描述了数据在连续时间域内如何被噪声逐渐破坏。
这个随机过程的逆向过程存在（更准确的描述：下面的逆向时间SDE具有与正向过程SDE相同的联合分布）为

\[ \begin{equation}d\mathbf{x}=[\mathbf{f}(\mathbf{x},t)-g^2(t)\nabla_{\mathbf{x}}\log p_t(\mathbf{x})]dt+g(t)d\bar{\mathbf{w}}\end{equation} \]

前面我们得到了扩散过程的逆向过程可以用一个SDE描述(逆向随机过程),事实上，存在一个确定性过程 (用ODE描述)也是它的逆向过程 (更准确的描述：这个ODE过程的在任意时刻 $t\in[0,T]$ 的状态的边缘分布 $p_t( \mathbf{x} ( t) )$ 与 SDE过程的相同

\[ \begin{equation}\mathrm d\mathbf x=\begin{bmatrix}f(\mathbf x,t)-\frac{1}{2}g^2(t)\nabla_{\mathbf x}\log p_t(\mathbf x)\end{bmatrix}\mathrm dt\end{equation} \]

其中，$\nabla_{\mathbf{x}}\log p_{t}(\mathbf{x})$ 叫做score function , 可以通过score match进行训练，也兼容普通的扩散模型噪声预测模型。

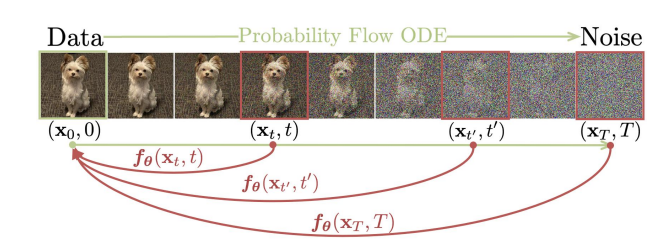
这个ODE称为概率流ODE(probability flow ODE,PF ODE,它沿着概率流的轨迹(也就是ODE的解函数) 建立了从噪声分布中的点$\mathbf{x}(T)\sim p_T(\mathbf{x}(T))$ 与到数据分布中的点 $\mathbf{x}(0)\sim p_T(\mathbf{x}(T))$的映射，也就是说PF ODE建立了高斯分布样本与数据分布样本的映射。

因此，采样时，把$s_{\theta}(\mathbf{x},t)\approx\nabla\log p_{t}(\mathbf{x})$ 代入PF-ODE, 仅需采样一次$\mathbf{x}(T)\sim p_T(\mathbf{x}(T))$, 然后可以确定性的解出一条从$\mathbf{x}(T)$到$\mathbf{x}(0)$的轨迹，这样的到的$\mathbf{x}(0)$的分布就是data分布。可以用ODE数值求解器来求解出$\mathbf{x}(0)$ ,例如欧拉法，Runge- Kutta法之类的数值方法。

Consistency Models

有了PF ODE,我们已经能做到采样一个高斯噪声，然后通过求解ODE，映射到数据。但求解ODE 仍然是一个迭代过程，要算很多次$\mathbf{s}_\theta(\mathbf{x},t)$ ,效率很低。我们能不能直接拟合出来这个ODE表示的映射 (也就是ODE的解函数),然后一步到位？Consistency models (一致性模型)就是相当于直接学了个ODE的解：任给某个轨迹上的点$(\mathbf{x}(t),t)$ ,一步inference得到$\mathbf{x}(0)$ !
首先我们回顾扩散过程SDE。在Consistency Models这篇论文里，为了最后的PF ODE形式的简单，他们采用了扩散项系数$g(t)=\sqrt{2t}$ ,漂流项 $\mathbf f(\mathbf x,t)$ 为0,

这样 $p_{t}(x)=p_{data}(x)\otimes\mathcal{N}(0,t^{2}I)$,其中$\otimes$是卷积操作，$\pi(x)=p_T(x)=\mathcal{N}(0,T^{2}I)$。用 score model $s_{\theta}(x,t)\approx\nabla\log p_{t}(x)$ 进行估计。在上述设置下，带入到1式和3式, 可以写作：

\[ \begin{align}\text{SDE:}\quad&dx_t=\sqrt{2t}d\boldsymbol{w}t\\\text{PF-ODE:}\quad&\frac{dx_t}{dt}=-ts_\theta(x_t,t)\end{align} \]

叫式5 为 empirical PF ODE。

对于式4的 SDE, 可以对两边进行$[0,T]$的积分：

\[ \begin{aligned}&\int_{0}^{T}dx_{t}=\int_{0}^{T}\sqrt{2t}dw_{t}\\&x_{T}-x_{0}=\mathcal{N}(0,\int_{0}^{T}2tdt)\\&x_{T}-x_{0}=\mathcal{N}(0,T^{2}I)\\&x_{T}=x_0+\mathcal{N}(0,T^2I)\end{aligned} \]

其中第二行利用的是随机微分方程SDE和基于 Ito 积分的性质，也可以理解为这个等式右侧是对正态分布进行积分，相当于无穷个带有系数 $\sqrt{2t}$ 的正态分布的相加，那么根据正态分布的线性性质，可以知道是无穷个$\mathcal{N}(0,2tI)$个正态分布相加，均值还是 0,方差为 $\int_0^T2tdt=T^2$。最后一行相当于一个加噪的过程，由于方差 $T^2$ 一般比较大，所以可以近似$x_T\sim\mathcal{N}(0,T^2I)$ ,同样的有任意时间步 $t$的加噪过程 $x_t=x_0+\mathcal{N}(0,t^2I)$ 。

从$\hat{x}_T\sim\pi(x)=\mathcal{N}(0,T^2I)$ 中采样初始噪声，然后使用 Euler/Heun 求解器求解式5, 可以得到一条采样轨迹$\{\hat{x}_t\}_{t\in[0,T]}$ 。为了数值稳定性，通常在 $t=\epsilon$ 处停止采样得到$\hat{x}_\epsilon$ , 可以近似认为满足分布$p_{data}(x)$。当$t$ 不是从 0 开始而是从 $\epsilon$ 开始，对应的加噪过程也有：

\[ \begin{aligned}&\int_{\epsilon}^{T}dx_{t}=\int_{\epsilon}^{T}\sqrt{2t}dw_{t}\\&x_{T}-x_{\epsilon}=\int_0^T\sqrt{2t}dw_t-\int_0^\epsilon\sqrt{2t}dw_t\\&x_{T}-x_{\epsilon}=\mathcal{N}(0,T^2I)-\mathcal{N}(0,\epsilon^2I)\\&x_{T}-x_{\epsilon}=\mathcal{N}(0,(T^2-\epsilon^2)I)\end{aligned} \]

由于$T>>\epsilon$, 所以先验分布仍然可以近似为 $x_T\sim\mathcal{N}(0,T^2I)$ 。并且，类似的有：

\[ \begin{equation}x_t=x_\epsilon+\mathcal{N}(0,(t^2-\epsilon^2)I)\end{equation} \]

定义

一致性函数

在给定概率流常微分方程(Probability Flow Ordinary Differential Equation, PFODE)的情况下，一致性函数可表示为下面的形
式：

\[ \begin{equation}f(\mathbf{x}_t,t)=\begin{cases}\mathbf{x}_\epsilon,&t=\varepsilon\\f(\mathbf{x}_{t'},t'),&t\in(\varepsilon,T],\forall t'\in[\varepsilon,T]\end{cases}\end{equation} \]

一致性模型的学习目标就是在给定PFODE上，得到一个神经网络使得任意相邻两个时刻的输出尽可能相等，进而逼近一致性函数。

如下图所示：

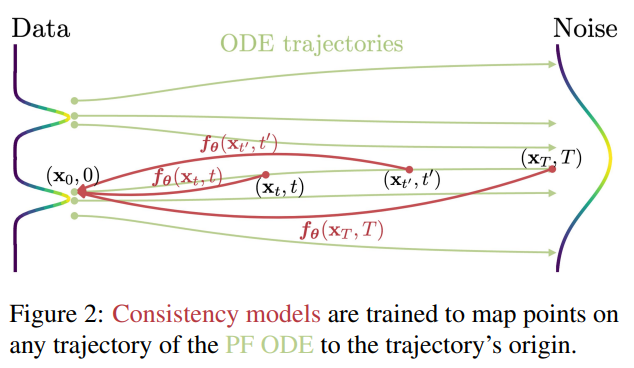
神经网络$f_{\theta}:\mathbb{R}^{N+1}\rightarrow\mathbb{R}^{N}$ 的形式为：

\[ \begin{equation}f_\theta(\mathbf{x}_t,t)\:=\:C_{\mathrm{skip}}(t)\mathbf{x}_t\:+\:C_{\mathrm{out}}(t)F_\theta(\mathbf{x}_t,t)\end{equation} \]

其中 $C_{\mathrm{skip}}$ 和$C_{\mathrm{out}}$是两个关于时间$t$的可微函数，保证$C_{\mathrm{skip}}(\epsilon)=1$ 和$C_{\mathrm{out}}(\epsilon)=0$,满足一致性函数的要求。

def denoise(self, model, x_t, sigmas, **model_kwargs):
    import torch.distributed as dist

    if not self.distillation:
        c_skip, c_out, c_in = [
            append_dims(x, x_t.ndim) for x in self.get_scalings(sigmas)
        ]
    else:
        c_skip, c_out, c_in = [
            append_dims(x, x_t.ndim)
            for x in self.get_scalings_for_boundary_condition(sigmas)
        ]

    rescaled_t = 1000 * 0.25 * th.log(sigmas + 1e-44)
    model_output = model(c_in * x_t, rescaled_t, **model_kwargs)
    denoised = c_out * model_output + c_skip * x_t
    return model_output, denoised

可以发现，在实现时引入多了一个 $C_{in}$，来限制输入图像，有点像LSTM的输入门。$C_{skip}$、$C_{out}$ 为人为设定，和时间相关，当$t$增加时，图像噪声水平增加，离采样终点越远远，$C_{skip}$ 的值会下降，$C_{out}$ 的值会上升，更少的输入信号 $x_t$ 被保留，更多依靠模型去进行预测。相反，当 $t$ 减少时，图像噪声水平下降，离采样终点越趋近，$C_{skip}$ 的值会上升，$C_{out}$ 的值会下降，更多的输入信号 $x_t$ 被保留，更少依靠模型去进行预测。至于 $C_{in}$，可以参考EDM算法。

采样

一致性模型 $f_\theta$ 训练好后，可以先从先验分布中采样$\hat{x}_T\sim\pi(x)=\mathcal{N}(0,T^2I)$ ,然后通过
$\hat{x}_\epsilon=\boldsymbol{f}_\theta(\hat{x}_T,T)$进行一步采样。
除此之外，还可以通过交替去噪和加噪 (在不同的时间点上进行一步加噪和一步去噪),提高样本
质量，即：

其中一步加噪使用的就是式6

训练Loss

一致性模型采用了让PF-ODE相邻两个时间点模型输出值差距最小化的方式实现利用神经网络逼近一致性函数的目标，损失函数可以写为：

\[ \begin{equation}\mathcal{L}^N(\theta)=\mathbb{E}[\|f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1})-f_\theta(\hat{\mathbf{x}}_{t_n},t_n)\|_2^2]\end{equation} \]

其中，$N$ 表示时间点设置的数目，$\hat{\mathbf{x}}_{t_n}$是通过一种ODE求解器获得的上一个时刻 $t_n$ 的图像，这里用$t_n$ 表示第 $n$ 个时间点对应的时间，$\mathbf{x} \sim p_{\mathrm{data}}, \mathbf{x} _{t_{n+ 1}}\sim \mathcal{N} ( \mathbf{x} , t_{n+ 1}^2\mathbf{I} ) , n\sim \mathcal{U} [ 1, N- 1]$ 且为整数。$N$ 是一个超参数，理论这个值越大，在PF-ODE上的路径点数目就会越多，两点之间越靠近，$\hat{\mathbf{x}}_{t_n}$ 的求解会更准，模型精度越好。实际上当$N$足够大以后，这个数值对模型性能影响已经不敏感。作者在这里并没有直接使用上面的损失函数形式，而是将上式后一项的 $f$ 的权重 $\theta$ 换成了模型的指数滑动平均值 (Exponential Moving Average, EMA) $\theta^-$。根据EMA的性质，给定衰减系数$0\leq\mu<1$,可得：

\[ \theta^-\leftarrow\text{stopgrad}(\mu\theta^-+(1-\mu)\theta) \]

此时，损失函数可写为：

\[ \begin{equation}\mathcal{L}^N(\theta,\theta^-)=\mathbb{E}[\|f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1})-f_{\theta^-}(\hat{\mathbf{x}}_{t_n},t_n)\|_2^2]\end{equation} \]

该式便是论文中损失函数的一种简化形式。采用EMA相当于用一个多轮加权平均的结果充当最终的模型，每一步不同的模型权重 $\theta$ 对其影响较小，因此$f_{\theta^-}$又被称作"目标模型"。采用EMA的原因是可以提升训练过程的稳定性，提升一致性模型的效果。有了损失函数的形式了，就可以考虑如何训练模型了。论文中给定了两种方法，一种是从已有模型切入，也即一致性蒸馏 (Consistency Distillation, CD),一种是从零开始训练一个新的一致性模型，也即一致性训练(Consistency Training, CT).

一致性蒸馏 (Consistency Distillation, CD)

一致性模型的训练可以从已有模型切入，比如采用score-based模型进行蒸馏。假设现在已经有一个模型$s_\theta(\mathbf{x}_t,t)$, 很自然地，通过模型预测出一个score的值，再通过欧拉法采样一步，就可以获得在PF-ODE路径上相邻点的位置。根据PF-ODE形式，很显然有：

\[ \begin{equation}\hat{\mathbf{x}}_{t_n}=\mathbf{x}_{t_{n+1}}-(t_n-t_{n+1})t_{n+1}s_\theta(\mathbf{x}_{t_{n+1}},t_{n+1})\end{equation} \]

代入10式损失函数中可得CD的损失函数形式为：

\[ \begin{equation}\mathcal{L}_{CD}^N(\theta,\theta^-) = \\ \mathbb{E}[\|f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1})-f_{\theta^-}(\mathbf{x}_{t_{n+1}}-(t_n-t_{n+1})t_{n+1}s_\theta(\mathbf{x}_{t_{n+1}},t_{n+1}),t_n)\|_2^2]\end{equation} \]

论文中给出了CD过程的算法步骤如下，结合损失函数来看不难理解。首先从数据中采样样本，均匀采样时间点$n$,根据时间加噪声。加完噪声后，采用ODE数值求解器获得上一个时间点的图像，紧接着计算损失函数并进行梯度反传。

其中，$\Phi$ 表示模型学习的"司机”, 可以是score，也可以是速度场等ODE迭代必须元素。$\lambda(\cdot)\in\mathbb{R}^+$是权重函数，作者设置恒等于 1, $d(\cdot,\cdot)$ 是衡量两个输入距离的指标，作者考虑了 L1、L2 和 LPIPS。需要注意的是，每一步需要同步更新EMA权重$\theta^-$的值。

一致性训练(Consistency Training, CT)

一致性模型难道一定要背靠一个现成的扩散模型吗？也可以从零开始训练一个一致性模型。可以发现，没有现成扩散模型的最大问题是 $\Phi$ 没了，没办法进行ODE的数值求解了。作者就给定了一个score-based模型$s_θ(x_t,t)$预测结果$\nabla \log p_t(x_t)$的平替，用这个平替让模型进行学习，进而替代$s_\theta(x_t,t)$。这个平替需要至少满足以下两个条件：

是$\nabla \log p_t(x_t)$的无偏估计
需要在训练过程中作为金标准，因此需要可以计算获得
基于上述两个条件，作者给出了平替的形式为：

\[ \begin{equation} \nabla_{x_t} \log p_t(x_t) = -\mathbb{E}\left[\frac{x_t - x}{t^2}|x_t\right] \end{equation} \]

其中，$x_t \sim \mathcal{N}(x,t^2\mathbb{I})$，$x \sim p_{data}$，可以发现。

论文中推导的前几步可能稍微难理解一点，在这里给大家全部补上。回忆一下概率论的基本概念，根据边缘概率密度与联合概率密度的关系，可得如下的等式：

$$
p_t(x_t) = \int p(x_t,x)dx = \int p(x_t|x)p_{data}(x)dx

接下来就是公式推导，公式推导的目的就是从score的定义出发，探索到底有没有一个关于score的无偏估计量。总体而言，宋博士在这里的推导过程相当清晰，几乎没有跳步，仅在开始两步稍微有点难度，在这里给大家一一分解。根据score的定义，$\log p_t(x_t)$关于$x_t$求导，实际上是一个复合函数求导！也即先对log求导，再对$p_t(x_t)$求导！心中牢记复合函数求导，则推导过程并不难理解，如下所示：

\[\begin{aligned} \nabla_{x_t} \log p_t(x_t) &= \frac{1}{p_t(x_t)} \cdot \nabla_{x_t}p_t(x_t) \quad \text{复合函数求导} \ \\&= \frac{\nabla_{x_t} \int p(x_t|x)p_{data}(x)dx}{p_t(x_t)} \ \\&= \frac{\int \nabla_{x_t}p(x_t|x)p_{data}(x)dx}{p_t(x_t)} \quad \text{莱布尼兹法则} \ \\&= \frac{\int \nabla_{x_t} \log p(x_t|x)p(x_t|x)p_{data}(x)dx}{p_t(x_t)} \quad \text{反用复合函数求导} \ \\&= \int \nabla_{x_t} \log p(x_t|x)\frac{p(x_t|x)p_{data}(x)}{p_t(x_t)}dx \ \\&= \int \nabla_{x_t} \log p(x_t|x)p(x|x_t)dx \quad \text{贝叶斯公式} \ \\&= \mathbb{E}{x_t\sim\mathcal{N}(x,t^2\mathbb{I}),x\sim p{data}}[\nabla_{x_t} \log p(x_t|x)|x_t] \quad \text{条件期望定义} \ \\&= -\mathbb{E}{x_t\sim\mathcal{N}(x,t^2\mathbb{I}),x\sim p{data}}\left[\frac{x_t-x}{t^2}|x_t\right] \quad \text{代入正态分布公式} \end{aligned}\]

通过推导可以发现，这个平替确实是score的无偏估计。

既然无偏估计出现了，对于原始损失函数，只需要把原来依靠模型预测值$s_\theta(\mathbf{x}_{t_{n+1}},t_{n+1})$预测的$\hat{\mathbf{x}}_{t_n}$直接写为平替形式
也即

\[ \begin{aligned}&\hat{\mathbf{x}}_{t_n}=\mathbf{x}_{t_{n+1}}-(t_n-t_{n+1})t_{n+1}s_\theta(\mathbf{x}_{t_{n+1}},t_{n+1})\\&\hat{\mathbf{x}}_{t_n}=\mathbf{x}_{t_{n+1}}+(t_n-t_{n+1})t_{n+1}\frac{\mathbf{x}_{t_{n+1}}-\mathbf{x}}{t_{n+1}^2}=\mathbf{x}_{t_{n+1}}+(t_n-t_{n+1})\frac{\mathbf{x}_{t_{n+1}}-\mathbf{x}}{t_{n+1}}\end{aligned} \]

所以，CT的损失函数形式为：

\[ \mathcal{L}_{CT}^N(\theta,\theta^-)=\mathbb{E}\left[\left\|f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1})-f_{\theta^-}\left(\mathbf{x}_{t_{n+1}}+(t_n-t_{n+1})\frac{\mathbf{x}_{t_{n+1}}-\mathbf{x}}{t_{n+1}},t_n\right)\right\|_2^2\right] \]

论文给出了基于CT损失函数的模型训练算法步骤，可以发现相比CD来说，主要不同点为相邻时刻(也即上一时刻)
的图像直接通过原始图像加噪而非ODE迭代获得 (与公式(16)等价)。

如何证明这个估计是正确有效的？假如我们已经有了一个ground truth score function
$\bold s_{\phi^*}(\bold x,t)=\nabla\log p_t(\bold x_t)$,可以证明这个估计的loss与给定ground truth score function的
loss之间的误差趋于0，即$\mathcal L_{CD}^N(\theta,\theta^-;\phi^*) - \mathcal L_{CT}^N(\theta,\theta^-)=o(\Delta t)$。作者通过泰勒展开证明
了这个结论。

在实验中，步数N随训练逐渐增加，可以加快收敛。

效果上，目前diffusion > CD > diffusion distillation > CT，（GAN的效果不太好比较，在有些数据集上，经过这么多年充分调教的GAN性能甚至再次反超diffusion，有的数据集上则不如CT）。作为单步方法的CD和CT打不过diffusion，其实可以理解，一方面这one-one mapping本身非常复杂，还是比较难拟合的；另一方面，consistency models训练方法是约束一条ODE轨迹上的相邻点输出相同，模型拟合不好的话，每一步的误差都会累积下来。

不过consistency model才刚刚提出不久，在训练方法上还有很多待研究的技术。而作为一种单步生成方法，相对于diffusion在性能上有着显著优势。

连续一致性模型

损失函数推导：以一致性蒸馏中 $\theta^- = \theta$为例

上述的一致性模型是基于离散时间序列 $\{t_0, \dots, t_N\}$，最典型的体现就是得用一个 ODE 求解器从 $\mathbf{x}_{t_{n+1}}$ 获得 $\mathbf{\hat{x}}_{t_{n}}$。ODE 求解器一定存在由于离散时间导致的截断误差，也就从理论上无法达到最优。离散到连续的转化主要体现在 ODE 求解器的迭代公式，在离散情况下, $d t$可以近似为 $\Delta t = t_{n+1} - t_n$, 在连续情况下我们有一个关于 $u$ 的连续时间函数 $t = \tau(u)$，所以 $\Delta t \approx \frac{d\tau(u)}{du}\Delta u = \tau'(u)\Delta u$。其中，$\Delta u \to 0$，也即

离散情形：
连续情形：
上述看似简单的改变会导致一致性模型学习目标（损失函数）的改变，一致性模型论文分了很多种情况进行推导讨论。让我们先考虑最简单的情况，先认为 $\theta^- = \theta$，也即不使用 EMA 权重，考虑一致性蒸馏场景。令 $\tau(u_n) = \tau\left(\frac{n-1}{N-1}\right), \quad n \in [1, N]$ 且 $n \in \mathbb{Z}, \quad u_n = \frac{n-1}{N-1}, \Delta u=\frac{1}{N-1}$，连续形式的损失函数可以改写为：

\[ \begin{equation} \mathbb{E}\left[\lambda(t_n)d\left(f_\theta(\mathbf{x}_{t_{n+1}}, t_{n+1}), f_\theta(\mathbf{x}_{t_{n+1}}, t_{n+1}) + t_{n+1}s_\phi f_\theta(\mathbf{x}_{t_{n+1}}, t_{n+1})\tau'(u_n)\Delta u, t_n\right)\right]\end{equation} \]

损失函数（16）是以一种“如连续”的状态，你说它是连续的，它毕竟没有显式的离散两个时间点的差了；你说它不是连续的，它毕竟还存在一个好像不那么和谐的 $\Delta u$，而且 $\tau'(u)$ 还是存在的。公式（16）虽然形式有了，但很难用代码实现。现在看来似乎没有什么办法了，毫无思路。毫无思路的时候，记住一个口诀：泰勒救我！ 光有泰勒显然还不够，我们回想一致性模型的学习目标是希望相邻两个时间点的输出尽可能的接近，最简单的想法就是，先无脑求一下下面这个式子：

\[ \begin{equation} f_\theta(\mathbf{\hat{x}}_{t_n}, t_n) - f_\theta(\mathbf{x}_{t_{n+1}}, t_{n+1})\end{equation} \]

很显然，直接求没法求，这个时候泰勒展开就能出场了:

\[ \begin{equation}\begin{aligned}&f_{\theta}(\hat{\mathbf{x}}_{t_{n}},t_{n})-f_{\theta}(\mathbf{x}_{t_{n+1}},t_{n+1})\\&=f_{\theta}(\mathbf{x}_{t_{n+1}}+t_{n+1}s_{\phi}(\mathbf{x}_{t{n+1}},t_{n+1})\tau^{\prime}(u_{n})\Delta u,t_{n}))-f_{\theta}(\mathbf{x}_{t_{n+1}},t_{n+1})\\&=f_{\theta}(\mathbf{x}_{t_{n+1}},t_{n+1})+t_{n+1}\frac{\partial f_{\theta}(\mathbf{x}_{t_{n+1}},t_{n+1})}{\partial\mathbf{x}_{t_{n+1}}}s_{\phi}(\mathbf{x}_{t_{n+1}},t_{n+1})\tau^{\prime}(u_{n})\Delta u\\&+\frac{\partial f_{\theta}(\mathbf{x}_{t_{n+1}},t_{n+1})}{\partial t_{n+1}}\underbrace{(t_{n}-t_{n+1})}_{-\tau^{\prime}(u_{n})\Delta u}-f_{\theta}(\mathbf{x}_{t_{n+1}},t_{n+1})+\underbrace{O((\Delta u)^{2})}_{\text{Lagrauge remainder}}\\&=t_{n+1}\frac{\partial f_{\theta}(\mathbf{x}_{t_{n+1}},t_{n+1})}{\partial\mathbf{x}_{t_{n+1}}}s_{\phi}(\mathbf{x}_{t_{n+1}},t_{n+1})\tau^{\prime}(u_{n})\Delta u \\&-\frac{\partial f_{\theta}(\mathbf{x}_{t_{n+1}},t_{n+1})}{\partial t_{n+1}}\tau^{\prime}(u_{n})\Delta u+O((\Delta u)^{2}) \end{aligned}\end{equation} \]

公式(18)暂时现放着，后面有用。还有一个式子似乎可以用泰勒展开，那就是距离度量函数$d$,也即：

\[ \begin{equation}d(f_\theta(\mathbf{x}_{t_{n+1}}),t_{n+1}),f_\theta(\hat{\mathbf{x}}_{t_n},t_n))\end{equation} \]

从始至终，影响我们无法进行实现连续一致性模型的"罪魁祸首"就是这个$\hat{\mathbf{x}}_{t_n}$, 既然看它不爽，那我
们对公式(19)的第二个输入$f_\theta(\hat{\mathbf{x}}_n,t_n)$在$f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1})$ 处进行泰勒展开。需要注意，这里实际上是一个"一元”函数的泰勒展开，有：

\[ \begin{equation}\begin{aligned}&d(f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1}),f_\theta(\hat{\mathbf{x}}_{t_n},t_n)) \\&=d(f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1}),f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1})) \\&+\frac{\partial d(f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1}),f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1}))}{\partial f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1})}(f_\theta(\hat{\mathbf{x}}_{t_n},t_n)-f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1}))\\&+\frac12(f_\theta(\hat{\mathbf{x}}_{t_n},t_n)-f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1}))^T\mathbf{G}(f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1}))(f_\theta(\hat{\mathbf{x}}_{t_n},t_n)-f_\theta(\mathbf{x}_{t_{n+1}},t_{n+1}))+O(|\Delta u|^3)\end{aligned} \end{equation} \]

这里引入了一个新的矩阵$\mathbf{G}(\mathbf{x})$,它的具体形式如下：

\[ [\mathbf{G}(\mathbf{x})]_{ij}:=\frac{\partial^2d(\mathbf{x},\mathbf{y})}{\partial y_i\partial y_j}\Big|_{\mathbf{y}=\mathbf{x}} \]

这个矩阵实际上就是黑塞 (Hessian) 矩阵，记录了一个标量输出的函数与输入向量所有元素可能的二阶偏导数。注意公式(20),有一些项是可以化简的：

对于距离度量$d(\mathbf{x},\mathbf{y})$,在同一位置的两点距离为0，也即$d(\mathbf{x},\mathbf{y})|_{\mathbf{y}=\mathbf{x}}=0$,所以有：
对于距离度量$d(\mathbf{x},\mathbf{y})$, 当两点距离位置相同时的梯度为0，也即$\nabla_\mathbf{y}d(\mathbf{x},\mathbf{y})|_\mathbf{y=\mathbf{x}}\equiv0$。所以有：