💡 ****

Flow-based Models

Normalizing Flow

Normalizing Flow 是一种基于变换对概率分布进行建模的模型，其通过一系列离散且可逆的变换实现任意分布与先验分布（例如标准高斯分布）之间的相互转换。在 Normalizing Flow 训练完成后，就可以直接从高斯分布中进行采样，并通过逆变换得到原始分布中的样本，实现生成的过程。（有关 Normalizing Flow 的详细理论）

从这个角度看，Normalizing Flow 和 Diffusion Model 是有一些相通的，其做法的对比如下表所示。从表中可以看到，两者大致的过程是非常类似的，尽管依然有些地方不一样，但这两者应该可以通过一定的方法得到一个比较统一的表示。

Continuous Normalizing Flow

Continuous Normalizing Flow（CNF），也就是连续标准化流，可以看作 Normalizing Flow 的一般形式。在传统的Normalizing Flows中，变换通常是通过一系列可逆的离散函数来定义的，而在CNFs中，这种变换是连续的，这使得模型能够更加平滑地适应数据的分布，提高了模型的表达能力。

设有 d 维空间中的数据 $x = (x^1, x^2, \dots, x^d) \in \mathbb{R}^d
$ 。CNF 有两个核心的研究对象：

概率密度路径

粒子在流动的过程中，其概率分布在不断地改变。定义概率密度路径 $p:[0,1]\times \mathbb R^d\to\mathbb R_{>0}$，其中 $p_t(\mathbf x)$ 表示 $t$ 时刻 $x$ 位置处的概率密度。称之为“路径”是因为 $t\mapsto p_t$ 可以视作无限维概率分布空间中的流形上的一条路径。

显然，对任意时刻 $t\in[0,1]$，概率密度 $p_t(\mathbf x)$ 都应满足归一化条件：$\int p_t(\mathbf x)\mathrm d\mathbf x=1$. 因此，区别于流体力学中一般的流（不要求密度是归一化的），我们称这种模型为归一化流；又由于时间是连续的，因此称为连续归一化流。

速度场与连续性方程

定义速度场为 $\mathbf u:[0,1]\times\mathbb R^d\to\mathbb R^d$，其中 $\mathbf u_t(\mathbf x)$ 表示 $t$ 时刻 $x$ 位置处粒子的运动速度。流体中的粒子沿着速度场 $\mathbf u$ 运动，引起概率密度的变化，因此 $\mathbf u_t(\mathbf x)$ 与 $p_t(\mathbf x)$ 之间一定存在某种关系，这个关系式称为连续性方程：

\[ \begin{equation}\frac{\partial}{\partial t}p_t(\mathbf x)+\nabla\cdot(p_t(\mathbf x)\mathbf u_t(\mathbf x))=0\end{equation} \]

直观上，连续性方程的第一项表示单位时间内 $x$ 位置处粒子的增加/减少量，第二项表示单位时间内 $x$ 位置处粒子的流出/流入量，显然粒子增加量就是流入量，因此连续性方程成立。熟悉随机微分方程的读者可能会发现，连续性方程其实就是 Fokker-Planck 方程在扩散项为零时的情形。

概率分布在向量场中进行变换这一过程可以用物理学中的传输行为来建模。这是因为不管概率分布如何变换，其在全体分布上的积分始终为 1，因此可以认为概率密度也是一个守恒的物理量，可以类比物理学中的质量、电荷等的传输行为进行建模。在物理学里，Continuity Equation是描述守恒量传输行为的偏微分方程。在适当条件下，质量、能量、动量、电荷等都是守恒量，因此很多传输行为都可以用连续性方程来描述，在高维情况中定义如下：

\[ \begin{equation}{{\frac{\partial p_{t}(x)}{\partial t}+\mathbf{div} \left(p_{t}(x) \mathbf{u}_{t}(x)\right)=0}} \end{equation} \]

$\operatorname{div}\left(p_{t}(x) \mathbf{u}_{t}(x)\right)$ 是向量场与概率密度的乘积的散度，表示概率流通过某个区域的净变化率。

值得注意的是，概率密度路径与速度场不是一一对应的关系，不同的速度场可以产生相同的概率密度路径。例如，给 $\mathbf u_t(\mathbf x)$ 加上散度为零的场（无源场），就得到了一个新的速度场，并且连续性方程依旧成立，所以概率密度路径不变。

向量场 是一个函数，它在空间中的每一点都分配一个向量。
在二维或三维空间中的每个点$ (x, y, z)$ 上，向量场会给出一个向量，这个向量可以表示速度、电场、磁场等任何有大小和方向的量。
可以用箭头图来可视化向量场，每个箭头表示一个向量，箭头的方向表示向量的方向，箭头的长度表示向量的大小。
散度（Divergence）是一个运算符，用来衡量一个向量场在空间中某一点的“发散程度”或者“汇聚程度”。它是一个标量值。
如果我们有一个向量场 $\mathbf{F}=(F_x,F_y,F_z)$（在三维空间中），它的散度定义为：
$\mathrm{div}(\mathbf{F}) = \nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}
$
简单来说，散度是将向量场的变化“压缩”成一个标量，描述了这个场在某点的“体积变化率”。

性质：Continuity Equation 是判断向量场 $v_t(x)$ 产生对应的概率密度路径 $p_t(x)$ 的 充分必要条件。如果向量场 $v_t(x)$ 和概率密度路径 $p_t(x)$ 满足 Continuity Equation ，则在CNFs 中该向量场 $v_t(x)$ 就能产生对应的概率密度路径 $p_t(x)$。

为什么说向量场 $v_t$ “生成” 了概率密度路径 $p_t$ ？为什么要用常微分方程 ODE 来表达？$v_t$ 是 $\phi_t$ 的导数（微分）。导数或者说微分，就是一个量随着另一个量极小变化时的变化，其实写成离散形式也好理解了，微分就是变化量： $ \phi't=\phi{t+\Delta t}-\phi_t$。就是从上一个时间点x的位置，怎么到下一个时间点x的位置，再知道初值 \(\phi_0=x$ 之后，就能从第一个点 “流” 到最后一个点，得到一个路径 $p_t$，所以说“向量场（\)\phi_t$ ODE 的解 $\phi'_t=v_t$）生成了一条概率路径”。而 ODE $d\phi_t/dt=v(z_t,t)$定义了一个向量场 $v$ 。

Probability path $p_t = \mathcal{N}(\mu_t, 1)$ from $p_0 = \mathcal{N}(0, 1)$ to $p_1 = \mathcal{N}(\mu, 1)$

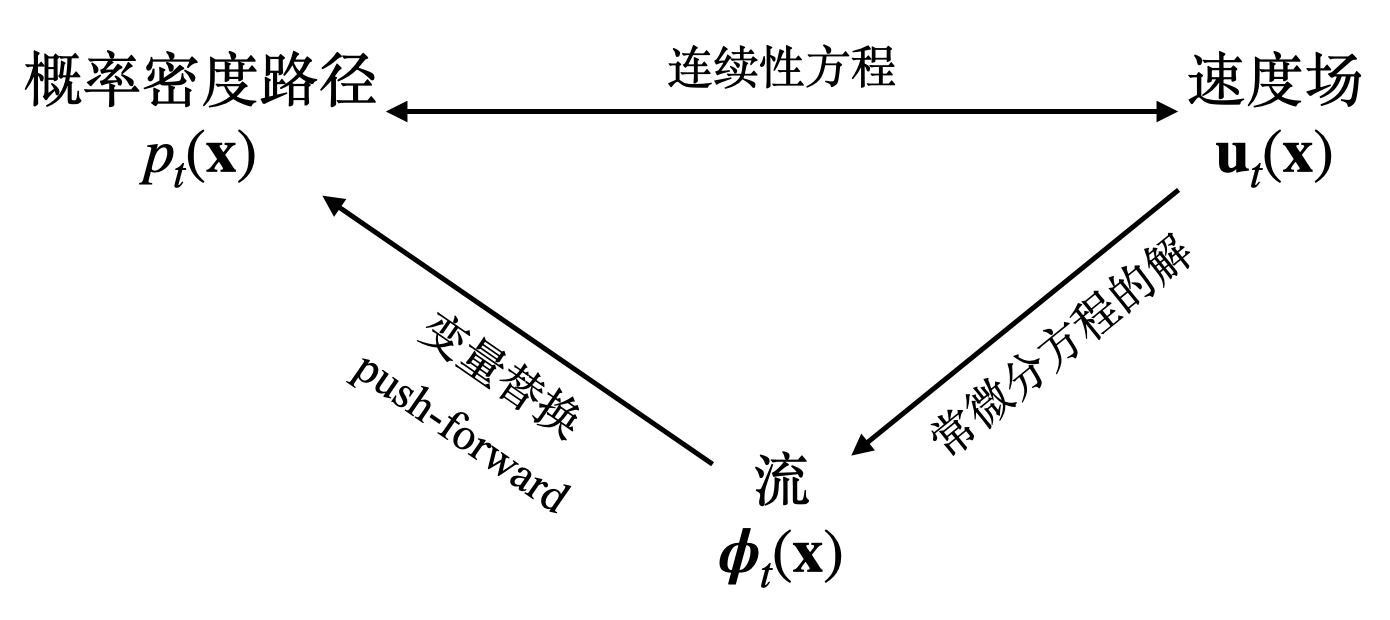
流与变量替换

粒子沿着速度场运动，得到的轨迹称为流。具体而言，流 $\boldsymbol\phi:[0,1]\times\mathbb R^d\to\mathbb R^d$是下述常微分方程的解：

\[ \begin{equation}\begin{aligned} \frac{\partial}{\partial t}\boldsymbol\phi_t(\mathbf x)&=\mathbf u_t(\boldsymbol\phi_t(\mathbf x))\\ \boldsymbol\phi_0(\mathbf x)&=\mathbf x \end{aligned}\end{equation} \]

其中 $\boldsymbol\phi_t(\mathbf x)$ 表示 0 时刻位于 $\mathbf x$ 处的粒子在 $t$ 时刻运动到的位置。换句话说，随着 $t$ 从 0 到 1 变化，$\boldsymbol\phi_t(\mathbf x)$ 形成了从 $\mathbf x$ 位置出发的粒子运动的轨迹。为了看得更清楚，可以对上式左右两边同时从 $0$ 到 $t$ 积分：

\[ \begin{equation}\boldsymbol\phi_t(\mathbf x)-\mathbf x=\int_0^t\mathbf u_s(\boldsymbol\phi_s(\mathbf x))\mathrm ds\end{equation} \]

左边表示从 $\mathbf x$ 出发的粒子在 $t$ 时间内的位移，右边是对速度的积分，自然也是位移。

💡 flow 的核心就是通过可逆变换在不同分布之间建立映射。$ϕ_t$就是这个变换函数，它告诉我们如何将一个分布中的点映射到另一个分布中的点，从而实现分布之间的转换。

根据流 $\boldsymbol\phi$ 的定义，$t$ 时刻位于 $\mathbf x$ 位置处的粒子在 $0$ 时刻的出发位置是 $\boldsymbol\phi_t^{-1}(\mathbf x)$，因此根据随机变量的变量替换公式，可以知道 $p_t(\mathbf x)$ 与 $\boldsymbol\phi_t(\mathbf x)$ 之间有关系：

\[ \begin{equation}p_t(\mathbf x)=p_0(\boldsymbol\phi_t^{-1}(\mathbf x))\left|\det\left[\frac{\partial\boldsymbol\phi_t^{-1}}{\partial\mathbf x}(\mathbf x)\right]\right|\end{equation} \]

简记作 $p_t=[\boldsymbol\phi_t]_\#(p_0)$，称作 push-forward 方程。

拓展（瞬时变量替换公式）：Push-forward 方程给出了 $0$ 时刻到 $t$ 时刻概率密度的变化。进一步地，Neural ODE 的作者还给出了描述概率密度变化的微分方程，称作瞬时变量替换公式：

\[ \begin{equation}\frac{\mathrm d}{\mathrm dt}\log p_t(\boldsymbol\phi_t(\mathbf x))+\nabla\cdot\mathbf u_t(\boldsymbol\phi_t(\mathbf x))=0\end{equation} \]

推导过程：计算 $p_t(\boldsymbol\phi_t(\mathbf x))$ 对 $t$ 的全导数：

\[ \begin{aligned}\frac{\mathrm d}{\mathrm dt}p_t(\boldsymbol\phi_t(\mathbf x))&=\left.\frac{\partial}{\partial t}p_t(\mathbf y)\right|_{\mathbf y=\boldsymbol\phi_t(\mathbf x)}+\left\langle\left.\nabla p_t(\mathbf y)\right|_{\mathbf y=\boldsymbol\phi_t(\mathbf x)},\frac{\partial \boldsymbol\phi_t(\mathbf x)}{\partial t}\right\rangle\\&=-\left.\nabla\cdot(p_t(\mathbf y)\mathbf u_t(\mathbf y))\right|_{\mathbf y=\boldsymbol\phi_t(\mathbf x)}+\left\langle\nabla p_t(\boldsymbol\phi_t(\mathbf x)),\frac{\partial \boldsymbol\phi_t(\mathbf x)}{\partial t}\right\rangle\\&=-\big[p_t(\mathbf y)(\nabla\cdot\mathbf u_t(\mathbf y))+\langle\nabla p_t(\mathbf y),\mathbf u_t(\mathbf y)\rangle\big]\Big|_{\mathbf y=\boldsymbol\phi_t(\mathbf x)}+\left\langle\nabla p_t(\boldsymbol\phi_t(\mathbf x)),\frac{\partial \boldsymbol\phi_t(\mathbf x)}{\partial t}\right\rangle\\\\&=-p_t(\boldsymbol\phi_t(\mathbf x))(\nabla\cdot\mathbf u_t(\boldsymbol\phi_t(\mathbf x)))-\left\langle\nabla p_t(\boldsymbol\phi_t(\mathbf x)),\mathbf u_t(\boldsymbol\phi_t(\mathbf x))\right\rangle+\left\langle\nabla p_t(\boldsymbol\phi_t(\mathbf x)),\frac{\partial \boldsymbol\phi_t(\mathbf x)}{\partial t}\right\rangle\\&=-p_t(\boldsymbol\phi_t(\mathbf x))(\nabla\cdot\mathbf u_t(\boldsymbol\phi_t(\mathbf x)))\end{aligned} \]

其中第二行是代入了连续性方程，第三行是将散度展开，最后一行是根据流的定义有 $\mathbf u_t(\boldsymbol\phi_t(\mathbf x))=\frac{\partial}{\partial t}\boldsymbol\phi_t(\mathbf x)$. 于是我们有：

\[ \frac{\mathrm d}{\mathrm d t}\log p_t(\boldsymbol\phi_t(\mathbf x))=\frac{1}{p_t(\boldsymbol\phi_t(\mathbf x))}\frac{\mathrm d}{\mathrm dt}p_t(\boldsymbol\phi_t(\mathbf x))=-\nabla\cdot\mathbf u_t(\boldsymbol\phi_t(\mathbf x)) \]

这就得到了瞬时变量替换公式。

Neural ODE 提出使用一个参数为 $\theta \in \mathbb{R}^p$ 的神经网络 $v_t(x; \theta)$ 来建模向量场 $v_t$，从而就能够计算出 flow $\phi_t$，来实现 CNF。

如果知道了这个向量场 $v_t$，那么通过求解这个ODE 就可以找到从初始概率分布到目标概率分布的连续路径，从而将简单分布转换成复杂分布。这个ODE可以采用欧拉方法来求解，从初始值$x_0$ 开始，使用下面的迭代公式来计算$z$在后续时间点的近似值：

\[ \mathbf{x}_{t+\Delta t}=\mathbf{x}_t+\Delta t\cdot v(\phi_t(\mathbf{x}_t)) \]

其中，$\Delta t = 1/N$ 是步长，$t=i/N$ 是采样时间点，$N$ 是最大采样步数，$x_t$ 是在时间 $t$ 的近似解。

也就是说，一旦我们得知从标准高斯分布到目标分布的变换向量场，就可以从标准高斯分布采样，然后通过上述迭代过程得到目标分布中的一个近似解，完成生成的过程。这和离散的 Normalizing Flow 是一致的。

综上所述，概率密度路径、速度场和流之间的关系可表示为下图：

在 Score-based Model 中，我们用随机微分方程（SDE）统一了 SMLD（Score Matching with Langevin Dynamics）和 DDPM，并且将 SDE 转化为了 ODE 概率流。也就是说，扩散模型同样能够用一个 ODE 来表示，因此，扩散模型也应当能够利用 CNF 的训练方式进行训练，这个训练的方式就是 Flow Matching。

Flow Matching

概述

在构建生成模型时，我们假设有一个未知的数据分布$q(x_1)$ (注意本文中的符号与扩散模型论文中常用的符号相反，本文 $x_{1}$ 表示真实数据，$x_0$ 表示随机噪声),我们能从其中采样出大量数据样本，但是不知道该分布的具体函数。
记 $p_t$ 为概率路径，而 $p_0=p$ 是一个简单的已知分布 (如标准高斯分布$p(x)\sim\mathcal{N}(0,\mathbf{I})$), 并令$p_1$ 在分布上大致与 $q$ 相等。Flow Matching 的目标就是去匹配这样一条目标概率路径，从而我们能够从$p_0$ ”流动“到$p_{1}$,实现生成。如何构造这样一条目标路径，稍后会介绍。

Flow Matching 的训练目标和 Score Matching 是比较类似的，学习的目标就是通过学习拟合一个向量场 $u_t$，使得能够得到对分布进行变换的概率路径 $p_t$，也就是下边这个公式：

\[ \begin{equation} \mathcal{L}(\theta)_{} = \mathbb{E}_{t \sim \mathcal{U}[0, 1]} \mathbb{E}_{x \sim p_t}\left[\| u_\theta(t, x) - u(t, x) \|^2 \right]. \end{equation} \]

其中 $θ$ 是模型的可训练参数，$t$ 在 0 到 1 之间均匀分布，$x\sim p_t(x)$ 是概率路径，$u_\theta(t, x)$ 是由模型表示的向量场。这个训练目标的含义为：利用模型 $θ$ 来拟合一个向量场 $u_\theta(t, x)$，使得最终通过学习到的 $u_\theta(t, x)$ 可以得到概率路径 $p_t(x)$，并且满足 $p_1(x)\approx q(x)$。

不过实际上这个公式并不实用，首先能够满足 $p_1(x)\approx q(x)$ 的概率路径是很多的，其次我们也不知道 $u(t,x)$ 究竟是什么东西，所以无法直接用来计算损失。

实际上概率路径有很多，如下图所示，在实际操作中，会选择一条具体的路径，也就是一个目标向量场$u_t$才具有实际意义。

从条件概率路径和向量场构造

虽然我们不知道 $p_t(x)$ 和 $u_t(x)$ 的具体形式，但是我们可以通过添加条件将其转换为可以求得的形式（可以类比在 DDPM 推导时将 $p(\mathbf{x}_{t-1}|\mathbf{x}_t)$ 转换为了 $p(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0)$, score matching中也有类似的转换过程，$\nabla\log p_t(\mathbf x)=\mathbb E_{p(\mathbf x_1\vert\mathbf x)}[\nabla\log p_t(\mathbf x\vert\mathbf x_1)]$）。也就是说，虽然 $u_t(x)$ 不知道，但是可以通过学习条件向量场 $u_t(x|x_1)$，使得最后通过这个向量场能够生成条件概率路径 $p_t(x|x_1)$, $x_1 \sim q_1$。由于我们可以获得数据样本，所以将$x_1$作为条件听起来非常合理，从而得出以下边际概率路径,

在这种情况下，条件概率路径 $p_{t\mid 1}$ 需要满足边界条件, 初始状态下条件分布等于先验分布；

终止状态下条件分布集中在$x_1$附近的一个很小的区域内；

\[ p_0(x\mid x_1)=p_0(x)\\\mathrm{and}\quad p_1(x\mid x_1)=\mathcal{N}(x;x_1,\sigma_{\min}^2I)\xrightarrow{\sigma_{\min}^2\rightarrow0}\delta_{x_1}(x) \]

第一个定理就是为了说明这个带条件的形式和不带条件的形式是等价的，也就是：

定理一： 给定向量场 $u_t(x|x_1)$，其能够生成条件概率路径 $p_t(x|x_1)$，那么对于任意分布 $q(x_1)$，满足某一特定形式（后文会给出）的边缘向量场 $u_t(x)$ 就能生成对应的边缘概率路径 $p_t(x)$。

证明： 首先，对于边缘概率路径 $p_t(x)$，有以下等式：

\[ \begin{equation}p_{t}\left( x \right)=\int p_{t}\left( x | z\right) q \left( z \right) dz \end{equation} \]

其中 $p_{t}\left( x | z\right) \(为条件分布，$q(z)\) 为隐变量分布，$p_{t}\left( x | z\right) $ 对应的速度场为 $u_{t}\left( x | z\right) \(。现在我们要考虑$u_{t}\left( x \right)\) 应该怎么被定义的问题。首先，我们考察一下连续性方程是否能被满足，这个是一切假设的前提。

\[ \begin{aligned}\frac{\partial}{\partial t} p_{t}\left( x \right)&=\frac{\partial}{\partial t} \int p_{t}\left( x | z\right) q \left( z \right) dz \\ &= \int \frac{\partial}{\partial t}\left[ p_{t}\left( x | z\right) q \left( z \right) \right] dz &\mathrm{Leibniz~integral~rule}\\& = \int \left[ \frac{\partial}{\partial t} p_{t}\left( x | z\right) \right] q \left( z \right) dz\end{aligned} \]

考虑到条件分布下的连续性方程 $\frac{\partial}{\partial t} p_{t}\left( x | z\right)=-\nabla\left( u_{t}\left( x | z\right) \cdot p_{t}\left( x | z\right) \right)$, 带到上式可得，

\[ \begin{equation}\begin{aligned}\frac{\partial}{\partial t} p_{t}\left( x \right) &= -\int \left[ \nabla\left( u_{t}\left( x | z\right) \cdot p_{t}\left( x | z\right) \right) \right] q \left( z \right) dz \\&= -\nabla \int u_{t}\left( x | z\right) p_{t}\left( x | z\right) q \left( z \right) dz \end{aligned}\end{equation} \]

我们希望能得到(2)式，即

\[ \begin{equation}\nabla \int u_{t}\left( x | z\right) p_{t}\left( x | z\right) q \left( z \right) dz = \nabla \left( u_{t}\left( x\right) p_{t}\left( x\right) \right) \end{equation} \]

推导到这里， $u_t(x) $需要满足以下形式：

\[ \mathbf{{{ u_{t}(x)=\int u_{t}\left(x \mid z\right) \frac{{\color{purple}{ p_{t}(x \mid z)}} q(z) }{\color{purple} {p_{t}(x)}} d z}} } \]

也就是说，只要 $u_t(x)$ 满足上边等式中的形式，就可以用 $u(x|x_1)$ 和 $p(x|x_1)$ 取代 $u(x)$ 和 $p(x)$。

这个边缘向量场的定义应该是为了这盘醋（论文中的定理1）包的这个饺子，针对这个公式具体点说也就是在数据点 $x$ 处的向量场 $u_t(x)$ 是通过对所有可能的初始条件 $x_1$ 的条件向量场 $u_{t}\left(x \mid x_{1}\right)$ 加权积分得到的，权重是由条件概率密度 $p_t(x∣x_1)$ 和边缘概率密度 $p_t(x)$ 的比值决定的。

Conditional Flow Matching

虽然基于上述过程已经推导出了 $u_t(x)$ 的形式，但上述的积分依然不容易求解。因此作者给出了一种更容易求解的形式（如下所示），并且证明了下面这个损失函数与原本损失函数的等价性。

\[ \begin{equation} \mathcal{L}_{\mathrm{CFM}}(\theta) = \mathbb{E}_{t \sim \mathcal{U}[0, 1], z \sim q(z), x \sim p_t(x \mid z)}\left[\| u_\theta(t, x) - u_t(x \mid z) \|^2 \right]. \end{equation} \]

这样写的直觉是，如果(11)式是一个好的代理目标，那么我们直接对(11)式进行优化就行，因为很有可能在给定 $z$ 的情况下，条件速度场是可采样或者可解的，类似分数匹配的条件概率一样。

作者证明了 $\mathcal{L}_{CFM}$ 和 $\mathcal{L}_{FM}$的等价性，也就是说优化 $\mathcal{L}_{CFM}$ 等价于优化 LFM：

定理二： 假定对于所有 $x\in\mathbb{R}^d$ 且$t\in[0,1]$都有 $p_t(x)>0$，那么 $\mathcal{L}_{CFM}$ 和 $\mathcal{L}_{FM}$ 相差一个与 $θ$ 无关的常数，即有 $\nabla_\theta\mathcal{L}_\mathrm{FM}(\theta)=\nabla_\theta\mathcal{L}_\mathrm{CFM}(\theta)$。

证明： 因为优化目标是 $θ$，我们考察 $\nabla_{\theta}L_{CFM}\left( \theta \right)$，有

\[ \nabla_{\theta}L_{CFM}\left( \theta \right) =\nabla_{\theta} E_{t,p_{t}\left( x | z \right),q\left( z \right)}\left\| u_{\theta}\left( t,x \right) - u_{t}\left( x | z \right)\right\|^{2} \\ =\nabla_{\theta} E_{t,p_{t}\left( x | z \right),q\left( z \right)} \left[ u_{\theta}\left( t,x \right)^{2} - 2 \cdot u_{\theta}\left( t,x \right) \cdot u_{t}\left( x | z\right) + u_{t}\left( x | z\right)^{2}\right] \\ =\nabla_{\theta} E_{t,p_{t}\left( x | z \right),q\left( z \right)}\left[ u_{\theta}\left( t,x \right)^{2} \right] - 2\nabla_{\theta} E_{t,p_{t}\left( x | z \right),q\left( z \right)}\left[ u_{\theta}\left( t,x \right) \cdot u_{t}\left( x | z\right) \right] \]

类似的，我们考察(6)式对于 $θ$ 的导数，有

\[ \nabla_{\theta}L_{FM}\left( \theta \right) =\nabla_{\theta} E_{t,p_{t}\left( x \right)}\left\| u_{\theta}\left( t,x \right) - u_{t}\left( x \right)\right\|^{2} \\ =\nabla_{\theta} E_{t,p_{t}\left( x \right)}\left[ u_{\theta}\left( t,x \right)^{2} \right] - 2\nabla_{\theta} E_{t,p_{t}\left( x \right)}\left[ u_{\theta}\left( t,x \right) \cdot u_{t}\left( x \right) \right] \]

对于两个式子的第一项有，

\[ \begin{aligned} \mathbb{E}_{p_t(x)}\left\Vert u_\theta(t,x)\right\Vert^2&=\int\left\Vert u_\theta(t,x)\right\Vert^2p_t(x)\mathrm{d}x \\ &=\int\left\Vert u_\theta(t,x)\right\Vert^2p_t(x|z)q(z)\mathrm{d}z\mathrm{d}x \\ &=\mathbb{E}_{q(z),p_t(x|z)}\left\Vert u_\theta(t, x)\right\Vert^2 \end{aligned} \]

所以现在的关键在于，以上两个式子的右边第二项有什么联系？我们继续化简

\[ \begin{aligned}\nabla_{\theta} E_{t,p_{t}\left( x \right)}\left[ u_{\theta}\left( t,x \right) \cdot u_{t}\left( x \right) \right] &=\nabla_{\theta} \int\int u_{\theta}\left( t,x \right)u_{t}\left( x \right)p_{t}\left( x \right)dxdt \\ &=\nabla_{\theta} \int\int u_{\theta}\left( t,x \right)\left[ \int \frac{u_{t}\left( x |z \right) p_{t}\left( x | z \right)}{p_{t}\left( x \right)} q\left( z \right)dz \right]p_{t}\left( x \right)dxdt \\ &=\nabla_{\theta} \int \int \int u_{\theta}\left( t,x \right)u_{t}\left( x |z \right) p_{t}\left( x | z \right)q\left( z \right)dxdtdz \\ &=\nabla_{\theta} E_{t,p_{t}\left( x | z \right),q\left( z \right)}\left[ u_{\theta}\left( t,x \right) \cdot u_{t}\left( x | z\right) \right]\end{aligned} \]

如此即证明了上述的定理，即

\[ \begin{equation}\nabla_{\theta}L_{FM}\left( \theta \right)=\nabla_{\theta}L_{CFM}\left( \theta \right) \end{equation} \]

这就意味着，优化(11)式和优化(7)式对于 $θ$ 来说是一样的，或者说你为了得到(7)式中的参数化速度场，你可以以(11)式为目标，构造条件速度场，然后用网络拟合 $u_{t}\left( x | z \right)$ 就行，至于拟合到的是什么没关系，实际推理的时候你可以直接把 $u_{\theta}\left( t,x \right)$ 当作 $u_t(x)$ 的近似来使用。

到这里，构造代理目标的目的就完成了。很有意思的是，我们在满足连续性方程的情况下构造的 $u_t(x)$ ，直接可以让我们用条件分布作为代理目标，来拟合边缘分布。事实上，用类似的思路，也可以证明在扩散模型SDE框架里，条件分数匹配的目标跟得分匹配的目标对于优化网络参数而言是一致的，具体可以参考苏剑林的《生成扩散模型漫谈（十八）：得分匹配 = 条件得分匹配》。

条件概率路径和向量场

上面我们已经证明了条件概率路径和条件向量场可以等价于边缘概率路径和边缘向量场，并且用 CFM 的方式进行训练和 Flow Matching 的效果是相同的。但现在 $u_t(x|z)$ 的形式依然是不知道的，因此我们需要进一步定义具体的条件概率路径的形式。就像 DDPM，我们需要定义具体的前向过程，才能基于这个过程进行训练。