结构光原理
基于结构光的三维成像,实际上是三维参数的测量与重现,主要是区别于纯粹的像双目立体视觉之类的被动三维测量技术,因而被称为主动三维测量。因为他需要主动去投射结构光到被测物体上,通过结构光的变形(或者飞行时间等)来确定被测物的尺寸参数,因此才叫做主动三维测量,嗯,相当主动。
首先,结构光的类型就分为很多种,既然是结构光,当然是将光结构化,简单的结构化包括点结构光,线结构光以及简单的面结构光等。复杂一点的结构化就上升到光学图案的编码了。结构光投射到待测物表面后被待测物的高度调制,被调制的结构光经摄像系统采集,传送至计算机内分析计算后可得出被测物的三维面形数据。其中调制方式可分为时间调制与空间调制两大类。时间调制方法中最常用的是飞行时间法,该方法记录了光脉冲在空间的飞行时间,通过飞行时间解算待测物的面形信息;空间调制方法为结构光场的相位、光强等性质被待测物的高度调制后都会产生变化,根据读取这些性质的变化就可得出待测物的面形信息。
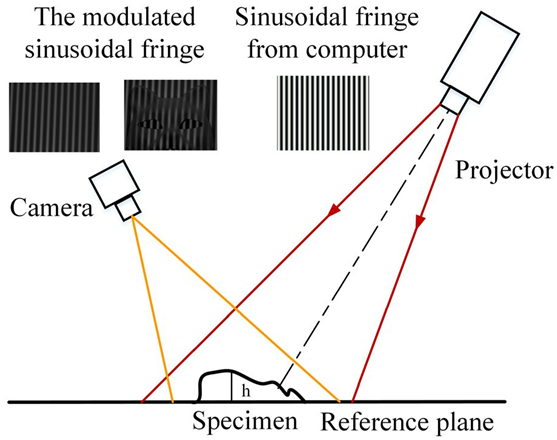
下面以一种应用广泛的光栅投影技术(条纹投影技术)为例来阐述其具体原理。条纹投影技术实际上属于广义上的面结构光。其主要原理如下图所示, 即通过计算机编程产生正弦条纹,将该正弦条纹通过投影设备投影至被测物,利用CCD相机拍摄条纹受物体调制的弯曲程度,解调该弯曲条纹得到相位,再将相位转化为全场的高度。当然其中至关重要的一点就是系统的标定,包括系统几何参数的标定和CCD相机以及投影设备的内部参数标定,否则很可能产生误差或者误差耦合。因为系统外部参数不标定则不可能由相位计算出正确的高度信息。
总体而言,结构光主要可以分为两类
1. 线扫描结构光;
2. 面阵结构光。
一般说结构光的时候都指代第二类,这里也主要关注面阵结构光。
1. 线扫描结构光
线扫描结构光较之面阵结构光较为简单,精度也比较高,在工业中广泛用于物体体积测量、三维成像等领域。
1.1 数学基础
先来看一个简单的二维下的情况:
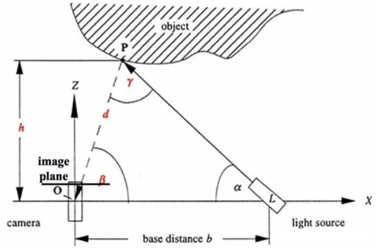
通过上图可以看到线扫描结构光装置的一个基本结构。主动光源L缓慢扫过待测物体,在此过程中,相机记录对应的扫描过程,最后,依据相机和光源在该过程中的相对位姿和相机内参等参数,就可以重建出待测物体的三维结构。
其中, \(α\) 为投影装置的朝向。 \(β\) 则需要通过对应像素的像素坐标 \(μ\)和焦距\(f\)来确定。最终可知\(P\)点的三维坐标为:\(P=(d\cdot cos\beta, d\cdot sin\beta)^T\), 将之推广至三维空间中:
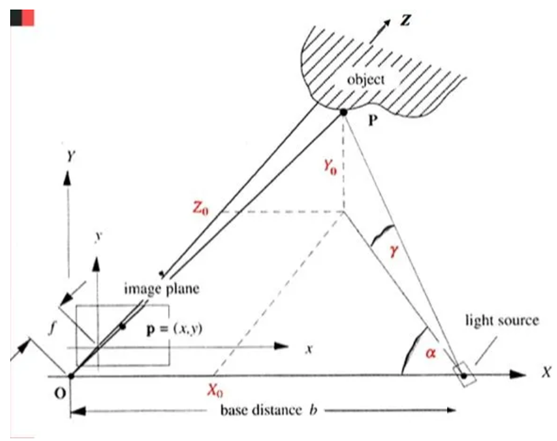
可得
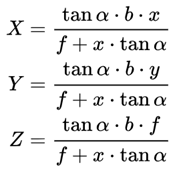
可以看到,三维空间中的情形和之前的二维空间类似,作为俯仰角的 \(γ\)并没有出现在公式中。
2. 面阵结构光
面阵结构光大致可以分为两类:随机结构光和编码结构光。随机结构光较为简单,也更加常用。通过投影器向被测空间中投射亮度不均和随机分布的点状结构光,通过双目相机成像,所得的双目影像经过极线校正后再进行双目稠密匹配,即可重建出对应的深度图。如下图为某种面阵的红外结构光。

随机结构光这里就不再说了,因为和普通双目算法是很相似的。一些额外的考虑就是是否给相机加装滤光片、光斑的密度要到什么程度等硬件和光学的问题了。
这里主要讨论编码结构光。编码结构光可以分为两类:
1. 时序编码;
2. 空间编码。
时序编码
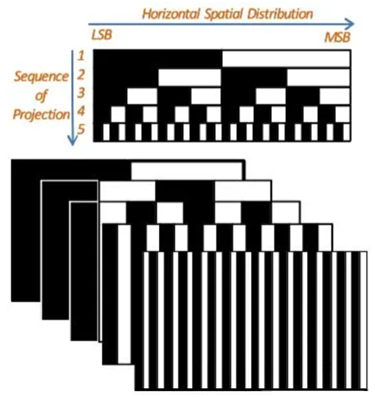
如上图,时序编码结构光即为在一定时间范围内,通过投影器向被测空间投射一系列明暗不同的结构光,每次投影都通过相机进行成像。假设共有n张影像,并设被阴影覆盖的部分编码值为1,未被覆盖的部分编码值为0。此时,每个像素都对应唯一一个长度为n的二进制编码,双目影像搜索匹配像素的问题就变成了查找具有相同编码值的像素。如果双目图像已经进行了极线校正,那么所投影的结构光只需要在x方向上不具有重复性即可。
优点:
· 高精度;
缺点:
· 只适用于静态场景;
· 需要拍摄大量影像。
空间编码
为满足动态场景的需要,可以采用空间编码结构光。前面谈到了随机结构光,就是不带编码信息,投影随机纹理,而这里讨论的空间编码结构光特指向被测空间中投影经过数学编码的、一定范围内的光斑不具备重复性的结构光。由此,某个点的编码值可以通过其临域获得。其中,包含一个完整的空间编码的像素数量(窗口大小)就决定了重建的精度。