目标检测的遮挡问题概述 -

Soft-NMS/DIoU-NMS

soft-nms参考：

可以看到，Soft-NMS与传统NMS的区别在于对score分数调整的处理。如果是传统的NMS操作，那么当$B$ 中的 $b_i$ 和 $\mathbf{M}$ 的IoU值大于阈值 $N_t$，那么就从 $B$ 和 $S$ 中去除该box；对于Soft-NMS而言是先计算 $\mathbf{M}$ 与 $b_i$ 的IoU，然后IoU经过一个函数输出最后与 $s_i$ 相乘最终得到box的分数。

其中 $s_i$ 的score遵循IoU越大，分数越低的原则（IoU越大，越可能是背景），所以$s_i$ 定义如下：

考虑到上式是不连续的，并且当达到N_t的NMS阈值时会施加突然的惩罚，如果惩罚函数是连续的，那将是理想的，否则它可能导致检测结果的排序列表的突然改变（集合D中的score出现断层跳跃现象）。所以 $s_i$ 的更新公式修改为如下：

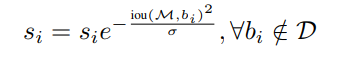
这样就避免了检测结果中的score会出现突然间的跳跃现象。

DIoU-NMS需要了解DIoU，它两在同一篇论文被提出，关于DIoU知识:

在传统NMS中，IoU指标常用于抑制冗余检测盒，其中重叠区域是唯一因素，对于遮挡情况经常产生错误抑制。 DIoU-NMS将DIoU作为NMS的准则，因为在抑制准则中不仅应考虑重叠区域，而且还应考虑两个box之间的中心点距离，而DIoU就是同时考虑了重叠区域和两个box的中心距离。对于score最高的预测box $M$，可以将DIoU-NMS 的 $s_i$ 更新公式正式定义为:

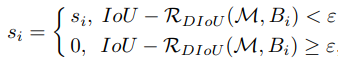
其中通过同时考虑IoU和两个box的中心点之间的距离来删除box $B_i$，$s_i$ 是分类得分，ε是NMS阈值。DIoU-NMS建议两个中心点较远的box可能位于不同的对象上，不应将其删除(这就是DIoU-NMS的与NMS的最大不同之处)。

RepLoss

问题引入

常见的遮挡问题可以再被细分为主要两类

类间遮挡，即目标被其他类遮挡住。举个例子，一个行人遛狗，人体下半部分就可能被狗狗遮住
类内遮挡，目标物体被同类遮挡住，在我们问题里面也就是行人遮挡。
我们思考一下行人遮挡会对检测器造成什么影响。假设我们目标行人是 T，旁边被另外一个行人 B 所遮挡。那么 B 的真实框会导致我们对 T 的预测框 P，往 B 去移动 (shift)，造成类似下图的情况

另外我们再考虑下目标检测常用的后处理 NMS，非极大值抑制。NMS 操作是为了抑制去除掉多余的框。但是在行人检测中，NMS 操作会带来更糟糕的检测结果。还是刚刚的例子，我对 T 有一个预测框 P，但因为距离 B 靠的太近，我可能会被 B 的预测框给抑制，导致行人检测中出现漏检。这也从另外一个侧面反映出行人检测对 NMS 阈值的敏感性，阈值太低了会带来漏检，阈值太高了会带来假正例（即标出错误的目标）

因此如何稳定的检测出群体中个体行人是行人检测器的关键。

现有的方法仅仅要求预测框尽可能靠近目标框，而没有考虑周围附近的物体。受磁铁同性相斥，异性相吸的原理，我们提出了一种 RepLoss 新的损失函数

该损失函数在要求预测框 P 靠近目标框 T(吸引) 的同时，也要求预测框 P 远离其他不属于目标 T 的真实框 (排斥) 该损失函数很好的提升了行人检测模型的性能，并且降低了 NMS 对阈值的敏感性

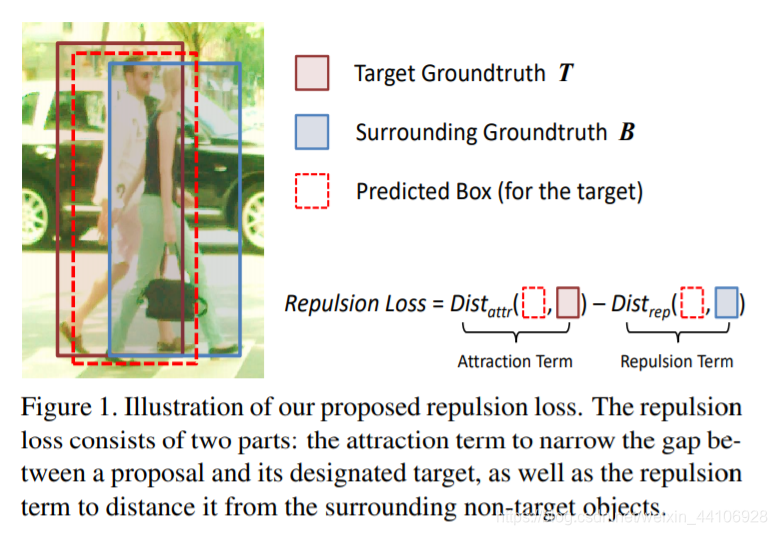
Repulsion Loss

前面分析了这么多错误，现在才是重头戏 Repulsion Loss 主要由三部分构成

\[ L = L_{Attr} + \alpha*L_{RepGT} + \beta*L_{RepBox} \]

$L_{Attr}$ 是为了预测框更接近真实框 (即吸引)

$L_{rep}$ 则是为了让预测框远离周围的真实框 (即排斥)

参数α和β用于平衡两者的权重

我们设 $P(lP , tP , wP , hP)$ 为候选框, $G(lG, tG, wG, hG) $为真实框

$P_+$ 为正候选框集合，正候选框的意思是，至少与其中一个真实框的 IoU 大于某个阈值，这里是 0.5, g = {G} 是真实框集合

Attraction term

这一项 loss 在其他算法也广泛使用，为了方便比较，我们沿用 smoothL1 Loss

\[ B^P是根据预测框P回归调整得来的 \\ G^P_{Attr}则是与预测框P有最大IoU的真实框 \\ G^P_{Attr} = arg max_{G∈g} IoU(G, P) \]

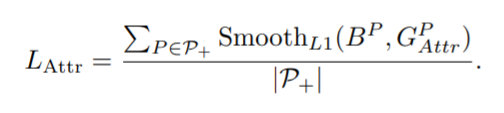
Repulsion Term (RepGT)

RepGT loss 设计是为了远离非目标的真实框对于一个候选框 P，其排斥对象被定义为，除去本身要回归目标的真实框外，与其 IoU 最大的真实框

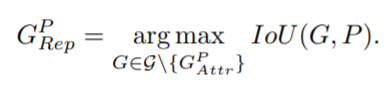
受 IoU loss 启发，我们定义了一个 IoG

\[ IoG(B, G) = {area(B∩G) \above{1pt} area(G)} \]

损失定义如下

这里没有采用 smooth l1 loss 而是 smooth ln loss，其公式如下

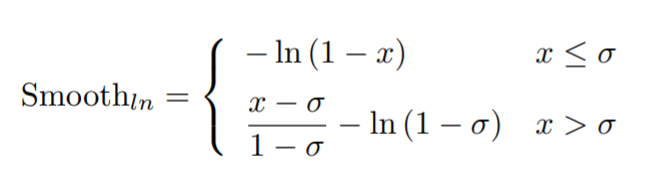
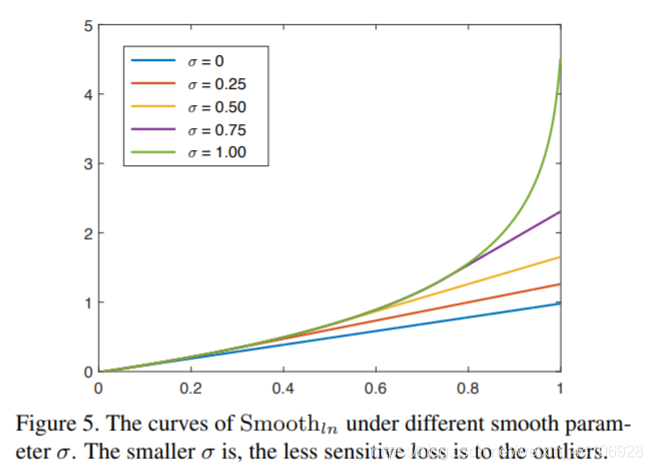
不同平滑系数，最后陡峭程度不一样。当一个候选框 P 与非目标的真实框重叠越多，其惩罚也越大。

Repulsion Term (RepBox)

这项损失是针对人群检测中，NMS 处理对阈值敏感的问题我们先将 P + 集合划分成互斥的 g 个子集（因为一共有 g 个目标物体）

\[ P+ = P1 ∩ P2 ∩ . . . ∩ P|G \]

然后从两个不同子集随机采样，分别得到两个互斥集合的预测框，即

\[ Pi ∈ Pi \space ,\space Pj ∈ Pj (where \space i, j = 1, 2, . . . , |G|, and \space i \not = j) \]

我们希望这两个互斥集合出来的回归框，交叉的范围尽可能小，于是有了 RepBox loss，公式如下

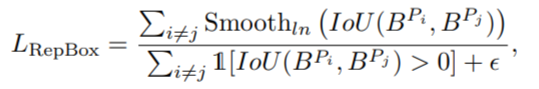
其中分母的 I 是 identity 函数，即

\[ y=x \]

这里限制大于 0，为了避免分式除 0，我们这里加了个ϵ 极小值上面依旧采用 Smooth ln 函数来计算。

距离函数选择

在惩罚项中，我们分别选择了 IoG 和 IoU 来进行度量。其原因是 IoG 和 IoU 把范围限定在了 (0, 1)，与此同时 SmoothL1 是无界的。如果 SmoothL1 用在 RepGT 中，它会让预测框与非目标的 gt 框离的越远越好，而我们的初衷只是想减少交叉部分，相比之下，IoG 更符合我们的思想

另外在 RepGT 中使用 IoG 而不使用 IoU 的原因是，IoG 的分母下，真实框大小 area(G) 是固定的，因此其优化目标是去减少与目标框重叠，即 area(B∩G)。而在 IoU 下，回归器也许会尽可能让预测框更大（即分母）来最小化 loss