NMS

过程：

根据分类概率从小到大排序ABCDEF
从最大概率F开始，F与A～E的IOU是否大于阈值
大于的扔掉，从剩下的当中继续重复2～3

import numpy as np


def nms(bbox, scores, Nt):
    if len(bbox) == 0:
        return []
    bboxes = np.array(bbox)
    x1 = bboxes[:, 0]
    y1 = bboxes[:, 1]
    x2 = bboxes[:, 2]
    y2 = bboxes[:, 3]

    area = (x2 - x1 + 1) * (y2 - y1 + 1)
    order = np.argsort(scores)
    res = []
    while order.size > 0:
        index = order[-1]
        res.append(bboxes[index])

        x11 = np.maximum(x1[index], x1[order[:-1]])
        y11 = np.maximum(y1[index], y1[order[:-1]])
        x22 = np.minimum(x2[index], x2[order[:-1]])
        y22 = np.minimum(y2[index], y2[order[:-1]])
        w = np.maximum(0, x22-x11+1)
        h = np.maximum(0, y22-y11+1)
        inter = w * h
        ious = inter / (area[index] + area[order[:-1]] - inter)
        left = np.where(ious < Nt)
        order = order[left]
    return res

Soft-NMS

NMS算法保留score最高的预测框，并将与当前预测框重叠较多的proposals视作冗余，显然，在实际的检测任务中，这种思路有明显的缺点，比如对于稠密物体检测，当同类的两个目标距离较近时，如果使用原生的nms，就会导致其中一个目标不能被召回，为了提高这种情况下目标检测的召回率，Soft-NMS应运而生。对于Faster-RCNN在MS-COCO数据集上的结果，将NMS改成Soft-NMS，mAP提升了1.1%。
它认为重叠较多的proposals也有可能包含有效目标，只不过重叠区域越大可能性越小。参见下图，NMS会将绿色框的score置0，而Soft-NMS会将绿色框的score由0.8下降到0.4，显然Soft-NMS更加合理。

那么问题来了，怎么建立Iou和score之间的联系呢，文章中给出的公式如下，

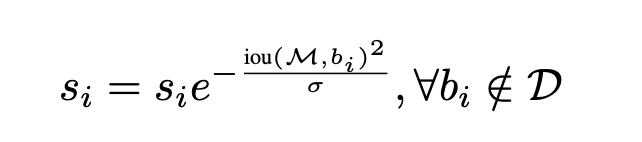
其中\(D\)表示所有保留的有效框集合，\(b_i\) 表示待过滤的第i个预测框，\(s_i\)为第i个预测框对应的分类score。这里使用了高斯函数作为惩罚项，当\(iou=0\)时，分类score不变，当\(0<iou<1\)时，分类score会做衰减。以上图为例，绿色框\(b_i\)和红色框M的iou大于0，经过Soft-NMS后该绿色框的分类score由0.8衰减到0.4，可以推断出，如果图中有第2个绿色框，且其与红色框的重叠区域更大时，那么这个新的绿色框的分类score可能由0.8衰减到0.01。

综上，soft-nms的核心就是降低置信度。比如一张人脸上有3个重叠的bounding box, 置信度分别为0.9, 0.7, 0.85 。选择得分最高的建议框，经过第一次处理过后，得分变成了0.9, 065, 0.55（此时将得分最高的保存在D中）。这时候再选择第二个bounding box作为得分最高的，处理后置信度分别为0.65, 0.45（这时候3个框也都还在），最后选择第三个，处理后得分不改变。最终经过soft-nms抑制后的三个框的置信度分别为0.9, 0.65, 0.45。最后设置阈值，将得分si小于阈值的去掉。

Softer-NMS

解决的问题算法

检测算法预测出来的proposals的坐标不一定准确；
分类score高不一定定位score高，也即classification confidence和 localization confidence不具有一致性。
针对上面的问题，（1）既然proposals的坐标不准确，那么即便NMS也无能为力了，所以需要重新设计坐标回归的方式；（2）既然分类score高不一定定位score高，那么NMS和Soft-NMS的做法（只基于分类score对proposals做排序）是不准确的，所以需要同时预测出检测框的定位score。

算法

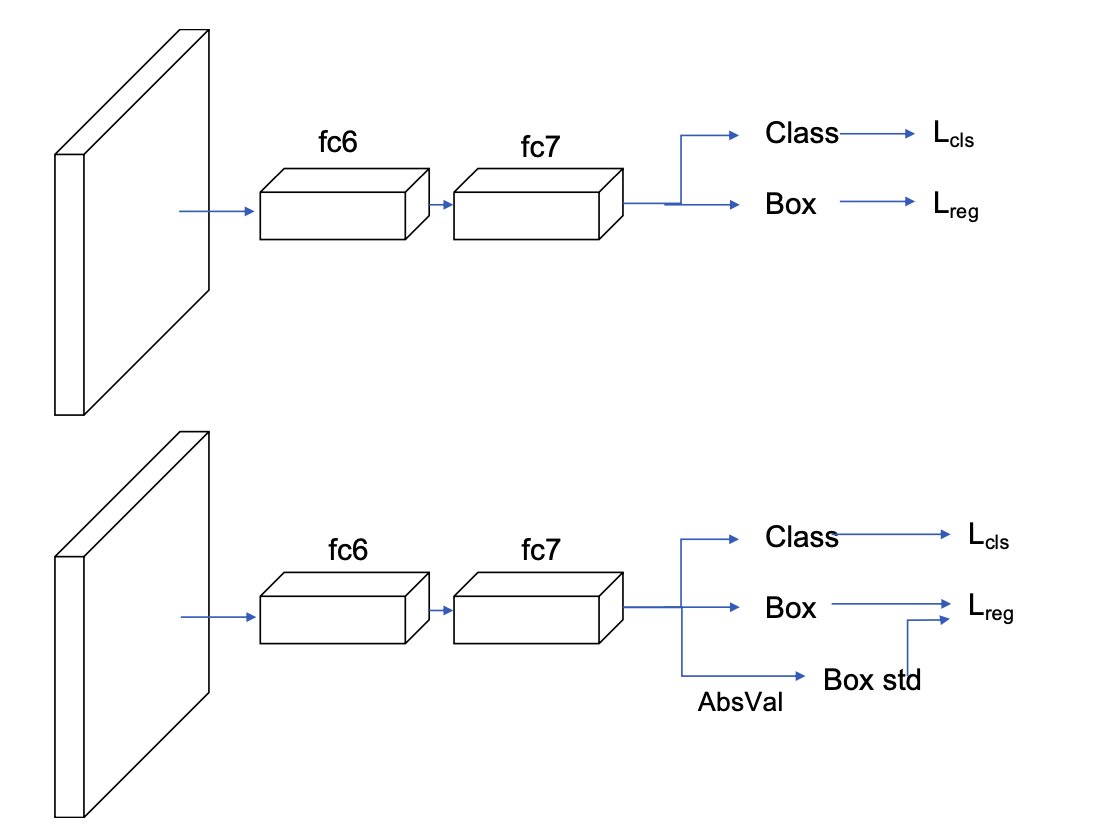
Softer-NMS的算法框架如下图，可以看出，它跟fast R-CNN是非常相似的，区别在于回归任务中多了一个Box std分支，这里需要解释一下，比如预测出的bounding box的坐标为\(x_1，y_1，x_2，y_2\)，该分支会预测出每个坐标的标准差，显然，当坐标的标准差越小时，表明预测得到的坐标值越可信，也即Box std分支用于表征定位任务的置信度。

在fast R-CNN中，作者使用的是均方误差函数作为定位损失，总的目的是让定位出的坐标点尽可能逼近groundtruth box。本文中为了在定位坐标同时输出定位score，使用了高斯函数建模坐标点的位置分布，公式如下，

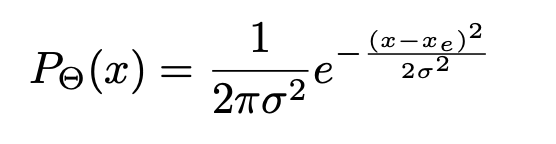
其中，\(x_e\)为预测的box位置，\(\sigma\)表示box位置的标准差，衡量了box位置的不确定性。因为groundtruth位置是确定的，所以groundtruth box的坐标为标准差为0的高斯分布，也即Dirac delta函数，公式如下，

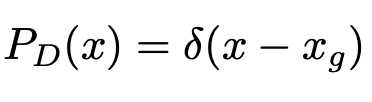
其中，\(x_g\)为groundtruth box的坐标。

回归任务的目的是让预测框尽可能逼近真实框，也即\(P_\theta(x)\)和\(P_D(x)\)为同一分布，衡量概率分布的相似性，自然而然会想到KL散度，关于KL散度的概念，大家可以参见维基百科，值得一提的是，KL散度本身具有不对称性，通常，在实际应用中为了使用对称性，使用的是KL散度的变形形式，但本文中没有这么做。对公式做化简后，最终的简化形式如下，

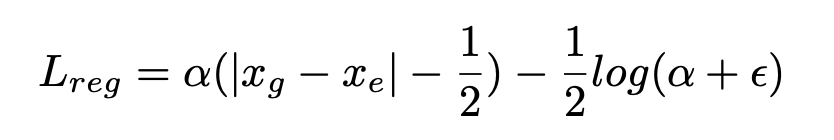
显然，softer-NMS基于回归出的定位confidence，对所有与M的IoU超过阈值\(N_t\)的proposals，使用加权平均更新其位置坐标，从而达到提高定位精度的目的。因为softer-NMS关注的是单个框的定位精度，而NMS和soft-NMS关注的是单个框的冗余性，显然关注点不同，所以softer-NMS可以和soft-NMS组合使用，此时效果更佳。

超过阈值的框根据 IoU 置信度加权合并多个框得到最终框，而不是直接舍弃