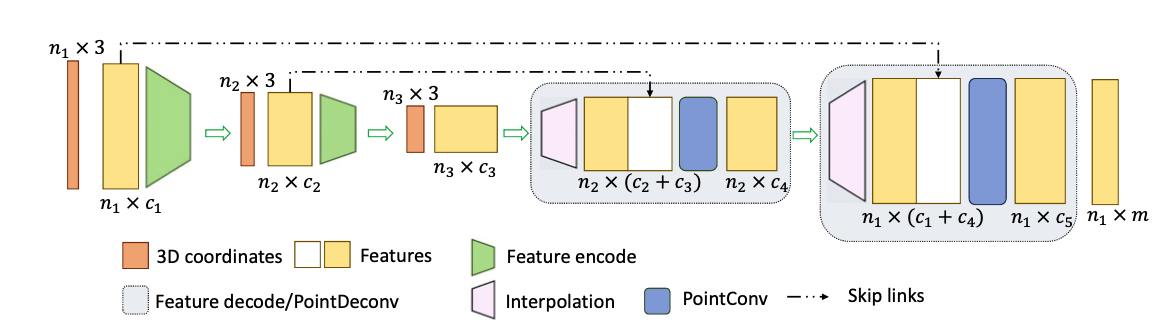
概括

这篇文章将卷积比较自然地拓展到点云的情形，思路很赞！

文章的主要创新点：“weight function”和“density function”，并能实现translation-invariance和permutation-invariance，可以实现层级化特征提取，而且能自然推广到其deconvolution的情形实现分割，在二维CIFAR-10图像分类任务中精度堪比CNN（表明能够充分近似卷积网络），达到了SOTA的性能。

缺点：每个kernel都需要由“kernel function”生成，而“kernel function”实质上是一个CNN网络，计算量比较大。

思想

察觉到：二维卷积中pixel的相对centroid位置与kernel vector的生成方式有关。

以二维卷积为例说明一下如何将卷积拓展到点云。这里只考虑使用一个kernel在一个location的一次卷积操作。

对于二维图像，我们可以将图像的pixels看作是一个点，那么图像就是整齐排列的点阵。每个point都有维度为\(C_{in}\)的特征向量（相当于图片是多通道的，一个通道对应于特征向量里的一个位置）。在二维卷积中，我们的kernel是“滑动”的，即我们在多个location的计算中共用一个kernel参数。这是为什么呢？我们如果认为这种共享参数的形式得益于整齐排列的points，那么这就是我们的PointConv的出发点了。

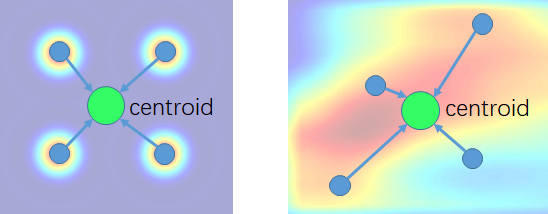
现在我们考虑一个point位置上的kernel是什么，在传统2D卷积中，这个值就是一个vector（\(𝐶_{𝑖𝑛}\)尺寸），如果points是正方形（2*2）整齐排列，那么我们可以认为kernel是\(2×2×C_{in}\) 的尺寸。但是我们现在不这么认为，我们认为kernel的尺寸是\(K×C_{in}\)（其中\(𝐾\)是输入点的个数，这里是4），这样有助于推广到点云的情形。

在2D图像中，我们不妨可以认为kernel是这样生成的：kernel在一个point上的值（vector），取决于point的位置。那么在2D图像中，这个生成vector的分布，则是4点的狄拉克分布，即在空间坐标中只在这4个位置下，才有对应的向量值。

我们推广开来，假设这个分布是实数值的连续分布，不妨叫它做“weight function”，那么在3D点云中，这个“weight function”的输入是3D坐标系x、y和z，它的输出则是一个vector（尺寸\(𝐶_{𝑖n}\)）。（在2D图像中，则\([f(0,0),f(1,0);f(0,1),f(1,1)]\) 组成了我们三维的kernel，尺寸\(2×2×C_{in} \(）。如果点的坐标是实数值（3D点云中其实就是实数值），那么我们点云的kernel尺寸就是\)4×C_{in}\)，即我们每个point都有一个vector kernel与它对应。我们的计算过程就是：每个point的feature与kernel vector做点积，最后把所有邻居点的点积的结果求和，得到的scalar就是我们一次卷积计算后的结果。

如果每个point的位置上是一个矩阵，那么相当于有多个kernel，最后得到的卷积结果不是scalar而是一个vector（有点像2D卷积中有多个卷积核的情形，输出就形成了多个channels）。

实现

在邻居点中实现卷积：

其中\(𝑊∈ℝ^{𝐾×(𝐶_{𝑖𝑛}×𝐶_{𝑜𝑢𝑡})}\)是\(𝐶_{𝑜𝑢𝑡}\)个kernel，\(𝐹_{𝑖𝑛}∈ℝ^{𝐾×𝐶_{𝑖𝑛}}\)是邻居的特征矩阵（一行一个），\(𝑆\) 是点密度的修正项（density scale），\(𝐹_{𝑜𝑢𝑡}\)是卷积后输出的vector。其中的kernel由“kernel function”生成，而“kernel function”接收x、y和z坐标输入，然后通过2D卷积（用1x1卷积核），得到一个尺寸为\(𝐾×𝐶_{𝑖𝑛}×𝐶_{𝑜𝑢𝑡}\)的tensor，就是\(𝑊\)。输出的\(𝐹_{𝑜𝑢𝑡}\)的空间坐标就是centroid的坐标。

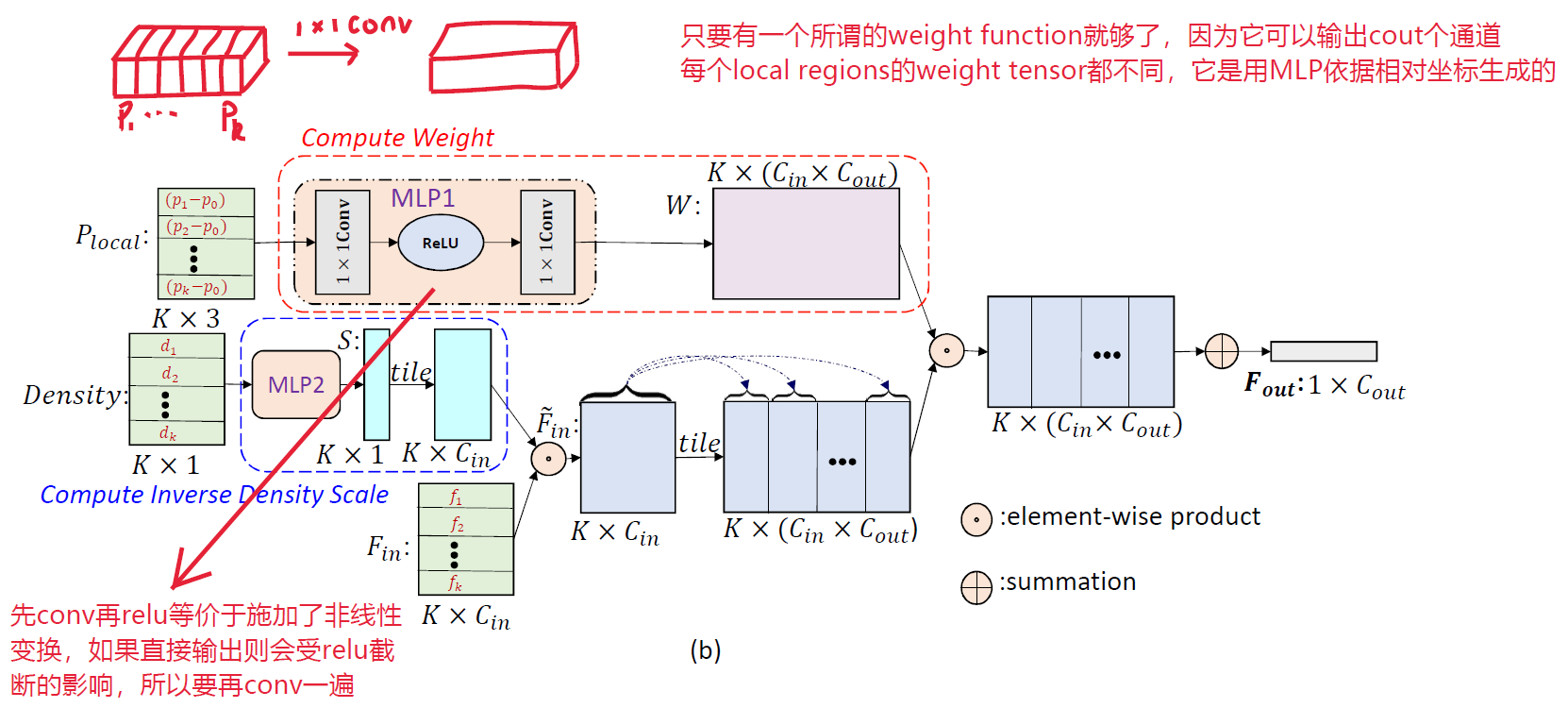
关于密度：作者首先使用“kernel density estimation”算法估计每一个点的密度，然后将得到的密度（一个点的密度是一个实数值，有\(K\)个点所以是一个1d vector）丢进MLP里非线性变换（丢进MLP里是为了让网络自己决定是否采用密度估计），估计密度是为了解决点云的非均匀采样导致的非均匀密度的问题。

作者发现原始版本的PointConv实现内存占用太大，提出了改进版本，在此不详述。

PointDeconv其实就是邻域3点线性插值上采样，与前面同级的特征concat，再使用PointConv。