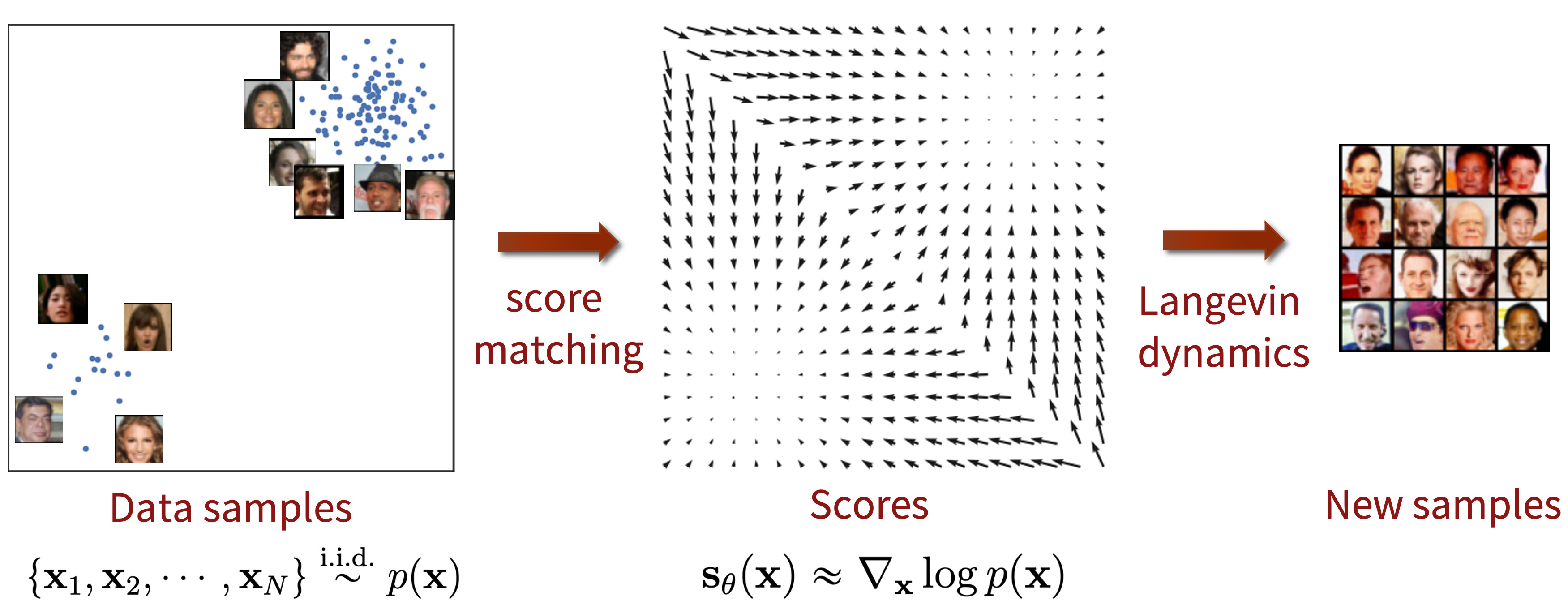
💡 Score based generative model SMLD的关键点：

正式开始介绍之前首先解答一下这个问题：score-based 模型是什么东西，微分方程在这个模型里到底有什么用？我们知道生成模型基本都是从某个现有的分布中进行采样得到生成的样本，为此模型需要完成对分布的建模。根据建模方式的不同可以分为隐式建模（例如 GAN、diffusion models）和显式建模（例如 VAE、normalizing flows）。和上述的模型相同，score-based 模型也是用一定方式对分布进行了建模。具体而言，这类模型建模的对象是概率分布函数 log 的梯度，也就是 score function，而为了对这个建模对象进行学习，需要使用一种叫做 score matching 的技术，这也是 score-based 模型名字的来源。

回答完这个问题其实就对基于分数的模型有一个大致的认识了，所谓的分数实际上就是一个和概率分布有关的函数，这类模型说到底也是在对概率分布进行建模。同时我们也可以从下面这张图直观地了解一下分数的物理意义：可以看到图中的等高线表示概率分布函数，箭头表示 score function，因为是梯度所以可以用垂直于等高线的矢量来表示。

Score Function 和 Score-based Models

考虑对一个数据集 $\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_N\}$ 的概率分布 $p(\mathbf{x})$ 进行建模，为了建模 $p(\mathbf{x})$，首先需要用一种方式来表示这个概率分布。我们可以使用一种通用的方式来表示这个概率分布：

为什么采样这样的式子以及后面的朗之万动力采样方程可以见这里：

\[ p_\theta(\mathbf{x})=\frac{\exp(-f_\theta(\mathbf{x}))}{Z_\theta} \]

这个公式来源于 energy-based models，其中 $f_\theta(\mathbf{x})$ 表示带有可学习参数 $θ$ 的函数（可以理解为某个神经网络）。因为 $f_\theta(\mathbf{x})$ 是概率分布函数，所以需要满足 $\int p_\theta(\mathbf{x})\mathrm{d}\mathbf{x}=1$，所以需要引入一个与 $θ$ 有关的归一化参数 $Z_\theta=\int\exp(-f_\theta(\mathbf{x}))\mathrm{d}\mathbf{x}$。

有了这个公式，我们就可以对 $θ$ 进行训练来对 $p(x)$ 进行极大似然估计：

\[ \max_{\theta}\sum_{i=1}^N\log p_\theta(\mathbf{x}_i) \]

然而这样做依然存在问题，那就是我们还不知道 $Z_\theta$ 具体是多少，对于一个任意的分布来说，这个归一化系数的值通常是无法求得的。这个问题已经有了几种不同的解决方案，例如 normalizing flow 通过保证网络可逆来使 $Z_\theta$ 恒定为 1，VAE 学习距离的变分下界等。在这里，score-based model 是通过改为对 score function 进行学习，比较巧妙地规避了 $Z_\theta$ 的问题。形式化地来说，score function 定义为：

\[ \mathbf{s}_\theta(\mathbf{x})=\nabla_\mathbf{x}\log p_\theta(\mathbf{x}) \]

因为 $Z_\theta$ 是常数，因此其本身并不产生任何梯度，所以有：

\[ \mathbf{s}_\theta(\mathbf{x})=\nabla_\mathbf{x}\log p_\theta(\mathbf{x})=-\nabla_\mathbf{x}f_\theta(\mathbf{x})-\nabla_\mathbf{x}\log Z_\theta=-\nabla_\mathbf{x}f_\theta(\mathbf{x}) \]

可以发现最后推导出的就是神经网络的梯度，这个各位读者肯定都不陌生，使用自动求导工具可以非常容易地得到。那么我们也可以写出优化目标（Fisher divergence）：

\[ \theta=\arg\min_{\theta}\mathbb{E}_{p(\mathbf{x})}[||\nabla_\mathbf{x}\log p(\mathbf{x})-\mathbf{s}_\theta(\mathbf{x})||_2^2] \]

写到这里就只有最后一个问题了：真实分布的 log 梯度 $\nabla_\mathbf{x}\log p(\mathbf{x})$ 实际上是未知的，因此这个优化目标不能直接用来对模型进行训练。为了解决这个问题，需要使用一种叫做 score matching 的方法。

分布学习：Score Matching

我们现在的目标是不使用真实分布 $p(\mathbf{x})$ 来计算上述的优化目标，为了简便起见，此处只讨论 $\mathbf{x}$ 为一元变量的情况。首先把 L2 的平方展开：

\[ \begin{aligned} &||\nabla_x\log p(x)-\mathbf{s}_\theta(x)||_2^2\\ =&||\nabla_x\log p(x)-\nabla_x\log p_\theta(x)||_2^2\\ =&\underbrace{(\nabla_x\log p(x))^2}_{\mathrm{const}}-2\nabla_x\log p(x)\nabla_x\log p_\theta(x)+(\nabla_x\log p_\theta(x))^2 \end{aligned} \]

第一项是常量，因为我们是要对 $\theta$ 求 $\arg\min$，所以这一项可以直接忽略掉。最后一项也可以通过数据集中的样本直接估计出来，因此现在只需要关注第二项。将第二项展开后使用分部积分法可以得到：

\[ \begin{aligned} &\mathbb{E}_{p(x)}[-\nabla_x\log p(x)\nabla_x\log p_\theta(x)]\\ =&-\int_{-\infty}^{\infty}\nabla_x\log p(x)\nabla_x\log p_\theta(x)p(x)\mathrm{d}x\\ =&-\int_{-\infty}^{\infty}\frac{\nabla_x p(x)}{p(x)}\nabla_x\log p_\theta(x)p(x)\mathrm{d}x\\ =&-\int_{-\infty}^{\infty}\nabla_xp(x)\nabla_x\log p_\theta(x)\mathrm{d}x\\ =&-p(x)\nabla_x\log p_\theta(x)\bigg|_{-\infty}^\infty+\int_{-\infty}^{\infty}p(x)\nabla_x^2\log p_\theta(x)\mathrm{d}x \end{aligned} \]

可以假设对于真实的数据分布，当 $|x|\rightarrow\infty$，有 $p(x)\rightarrow0$，所以最后结果的第一项为 0，继续推得：

\[ \mathbb{E}_{p(x)}[-\nabla_x\log p(x)\nabla_x\log p_\theta(x)]=\mathbb{E}_{p(x)}[\nabla_x^2\log p_\theta(x)] \]

最后得到总体的优化目标为：

\[ \begin{aligned} &\mathbb{E}_{p(x)}\left[||\nabla_x\log p(x)-\mathbf{s}_\theta(x)||_2^2\right]\\ =&2\mathbb{E}_{p(x)}\left[\nabla_x^2\log p_\theta(x)\right]+\mathbb{E}_{p(x)}\left[(\nabla_x\log p_\theta(x))^2\right]+\mathrm{const} \end{aligned} \]

对于多元的情况则是 $\mathbb{E}_{p(\mathbf{x})}\left[2\mathrm{tr}(\nabla\mathbf{x}^2\log p_\theta(\mathbf{x}))+||\nabla_\mathbf{x}\log p_\theta(\mathbf{x})||_2^2\right]+\mathrm{const}$。可以看到现在优化目标不包含真实分布 $p(x)$ ，可以直接用于优化。

这是最基本的 score matching 方法，后续为了在高维数据上进行加速还提出了 sliced score matching，这里就不展开介绍了。总之现在 score-based model 的训练问题也得到了解决，最后就是如何从训练好的分布中进行采样。

从分布采样：Langevin Dynamics

到这一步我们已经得到了 $\mathbf{s}_\theta(\mathbf{x})\approx\nabla\mathbf{x}\log p(\mathbf{x}) $，要从这样的一个梯度的分布中进行采样，可以通过 Langevin Dynamics（直译是朗之万动力学）过程实现。

朗之万动力学过程是一种马尔可夫链蒙特卡洛过程，具体来说，其首先从任意的先验分布中采样出初始状态 $\mathbf{x}_0\sim\pi(\mathbf{x}) $，然后进行迭代：

\[ \mathbf{x}_{i+1}\leftarrow\mathbf{x}_i+\epsilon\nabla_\mathbf{x}\log p(\mathbf{x})+\sqrt{2\epsilon}\mathbf{z}_i,\quad i=0,1,\cdots,K \]

其中 $ \mathbf{z}_i\sim\mathcal{N}(0,I) $，当 \(\epsilon\rightarrow0$ 且 $K\rightarrow\infty$，上述过程得到的 $\mathbf{x}_K$ 收敛到从 $p(\mathbf{x})$ 直接采样的结果。可以比较直观地理解这个迭代过程的含义：第一项 $\mathbf{x}_i$ 是上一个状态，第二项 $\epsilon\nabla\mathbf{x}\log p(\mathbf{x})$ 相当于沿着梯度的方向移动了 $\epsilon$ 单位，最后一项\) \sqrt{2\epsilon}\mathbf{z}_i$ 添加了一些随机扰动，应该是为了防止样本落入梯度比较小的位置。可以进一步从下面这个动图理解这一过程：

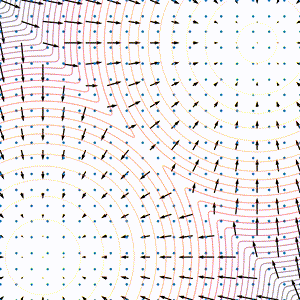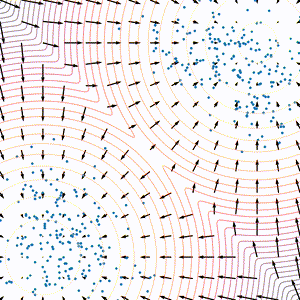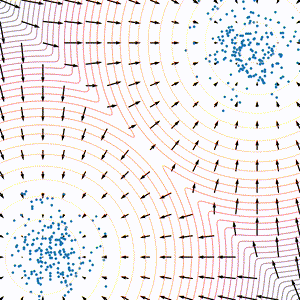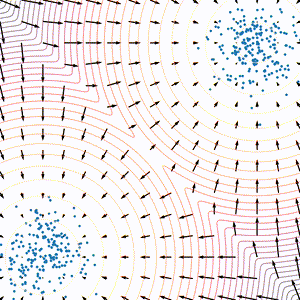
一般来说只要 $\epsilon$ 的取值足够小，且迭代步骤数量 $K$ 足够多，得到结果的误差就会比较小。同时从上式中可以发现，迭代过程中只使用了 $\nabla_\mathbf{x}\log p(\mathbf{x})$ 也就是 $\mathbf{s}_\theta(\mathbf{x})$ 而没有使用 $p(\mathbf{x})$，所以从学习到的 $\mathbf{s}_\theta(\mathbf{x})$ 即可完成采样。

存在的问题与改进方案

经过上面的几个步骤，score-based model 中最重要的几个问题其实已经解决了，我们能够通过 score matching 的过程对分布进行建模，也可以利用 Langevin dynamics 进行采样，如下图所示。不过这种做法依然存在一些问题，本章节将会介绍存在的问题和改进方案。

低概率密度区域建模不准确问题

根据 score matching 的过程，在对分布建模时优化的目标为：

\[ \mathbb{E}_{p(\mathbf{x})}\left[||\nabla_\mathbf{x}\log p(\mathbf{x})-\mathbf{s}_\theta(\mathbf{x})||_2^2\right]=\int p(\mathbf{x})||\nabla_\mathbf{x}\log p(\mathbf{x})-\mathbf{s}_\theta(\mathbf{x})||_2^2\mathrm{d}\mathbf{x} \]

可以看到等式右侧的 L2 损失被 $ p(\mathbf{x})$ 进行了加权，那么用这种方式进行优化会导致 $ p(\mathbf{x})$ 比较小的区域被忽略掉，从而无法在相应的范围内进行比较准确的建模。这个现象可以从下图得到一个比较直观的理解：对于最左侧的混合高斯分布，只有左下和右上的区域概率比较大，这些区域会在训练的过程中得到比较多的关注，而其他的大部分区域都被忽略，无法进行准确的建模。这限制了 score-based 模型得到比较好的结果。

Multiple Noise Pertubations

为了解决这个问题，一个比较符合直觉的方案就是通过一些方式使分布更加均匀。但是这样依然存在一个问题，举一个极端的例子，如果无限平均分布，让分布成为一个处处相等的均匀分布，这样学习到的分布对原始分布就没有充足的代表性。因此需要在这两者之间寻找一个平衡点，既不能让分布过于不平衡，使低频率区域的学习效果过差，同时也不能严重破坏原有分布，使学习到的分布与真实分布偏差过大。

实际上解决这个问题的方案相当简单，为了对分布进行平衡，可以使用各向同性高斯噪声对分布进行扰动（也就是这一节标题中的 pertubation）。一个扰动的示例如下图所示，直观上看其实类似于对概率密度进行了高斯模糊，处理之后概率分布变得比较均匀，从而能进行准确建模。同时，由于不同的分布需要的扰动程度是不同的，因此并不使用单一的高斯分布进行扰动，而是使用一系列扰动，这样就可以规避扰动程度的选择问题。

形式化地说，对于使用高斯噪声进行扰动的情况，可以使用 $L$ 个带有不同方差 $\sigma_1<\sigma_2<\cdots<\sigma_L$ 的高斯分布 $\mathcal{N}(0,\sigma_i^2I),i=1,2,\cdots$,$L$ 分别对原始分布 $p(\mathbf{x})$ 进行扰动：

\[ p_{\sigma_i}(\mathbf{x})=\int p(\mathbf{y})\mathcal{N}(\mathbf{x};\mathbf{y},\sigma_i^2I)\mathrm{d}\mathbf{y} \]

从 $p_{\sigma_i}(\mathbf{x})$ 中采样是比较容易的，和 diffusion 中的重参数化技巧类似：先采样$ \mathbf{x}\sim p(\mathbf{x})$，再计算 $\mathbf{x}+\sigma_i\mathbf{z}$，其中 $ \mathbf{z}\sim\mathcal{N}(0,I)$。

获得一系列用噪声进行扰动过的分布后，依然是对每一个分布进行 score matching，对于 $\nabla_\mathbf{x}\log p_{\sigma_i}(\mathbf{x})$ 得到一个与噪声有关的 score function $ \mathbf{s}_\theta(\mathbf{x},i)$。总体上的优化目标是对所有的这些分布 score matching 优化目标的加权：

\[ \sum_{i=1}^L\lambda(i)\mathbb{E}_{p_{\sigma_i}(\mathbf{x})}\left[||\nabla_\mathbf{x}\log p_{\sigma_i}(\mathbf{x})-\mathbf{s}_\theta(\mathbf{x},i)||_2^2\right] \]

对于加权权重的选择，通常直接指定 $\lambda(i)=\sigma_i^2$。这样我们就获得了一系列用不同的高斯噪声扰动过的分布，直观地看，扰动程度比较小的分布更接近真实分布，能在高概率密度的区域提供比较好的估计；扰动程度比较大的分布则能在低概率密度的区域提供比较好的估计，带有不同扰动程度的分布形成了一种比较互补的关系，有利于提高概率建模质量。

采样的过程依然是进行一系列迭代，不过因为有多个分布，所以需要依次对每个分布迭代一遍，相当于一共迭代 $L\times T$ 轮，得到最终的结果。这种采样方法叫做 Annealed Langevin Dynamics退火朗之万动力学，具体的采样算法可以参考这个链接的内容。

下面是退火朗之万动力学的算法流程图

Score-based Model小结

作为生成模型的一种，score-based model 也遵循学习+采样的范式，其学习过程使用 score matching 来间接学习分布，采样过程使用 Langevin dynamics 通过迭代过程进行采样（和 diffusion models 的采样过程有点类似）。在训练时由于低概率密度区域会有比较低的权重，所以这部分区域无法准确学习，为了解决这个问题，又使用 multiple noise pertubation 和 annealed Langevin dynamics 进行了改进。

常微分方程(ODE)和随机微分方程(SDE)简介

首先我们先介绍一些随机微分方程的基本知识以便理解。我们首先举一个常微分方程（ODE）的例子，例如下面的一个常微分方程：

\[ \frac{\mathrm{d}\mathbf{x}}{\mathrm{d}t}=\mathbf{f}(\mathbf{x},t)\quad\mathrm{or}\quad\mathrm{d}\mathbf{x}=\mathbf{f}(\mathbf{x},t)\mathrm{d}t \]

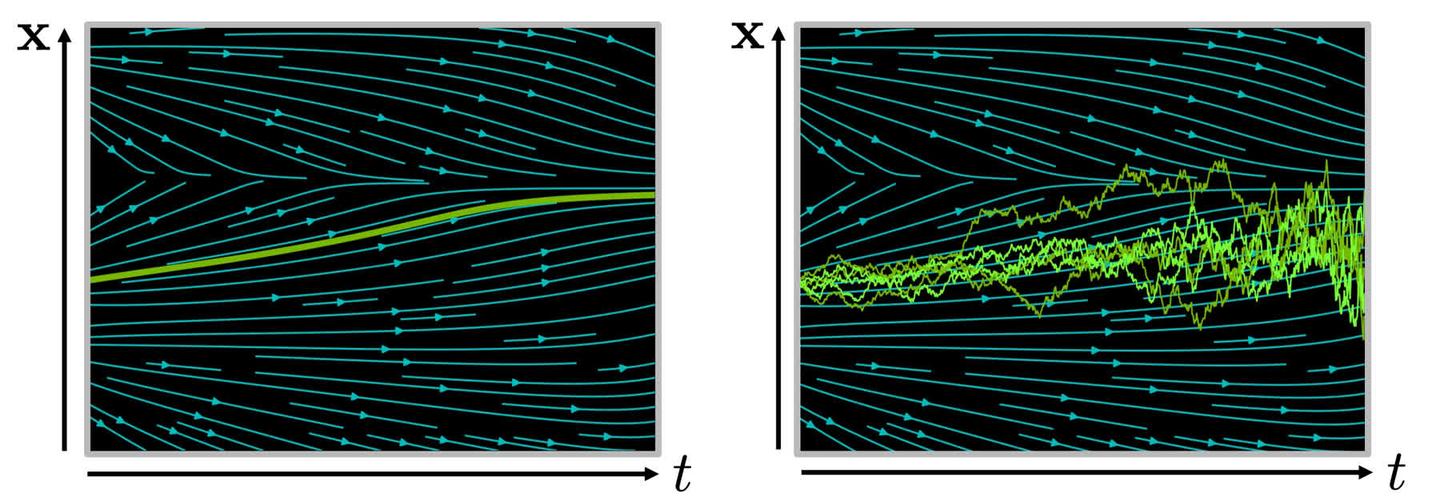
其中的 $\mathbf{f}(\mathbf{x},t)$ 是一个关于 $\mathbf{x}$ 和 $t$ 的函数，其描述了 $\mathrm{x}$ 随时间的变化趋势，如下面图中的左图所示。直观地说， $\mathbf{f}(\mathbf{x},t)$ 对应于图中的青色箭头，确定了某一个时刻的 $\mathbf{x}(t)$ 后，只要跟着箭头走就可以找到下一个时刻的 $\mathbf{x}(t+\Delta t)$。这个常微分方程可以得到解析解：

\[ \mathbf{x}(t)=\mathbf{x}(0)+\int_0^t\mathbf{f}(\mathbf{x},\tau)\mathrm{d}\tau \]

然而在实际应用中我们使用的 $\mathbf{f}(\mathbf{x},t)$ 通常是一个比较复杂的函数，例如神经网络，那么求出这个解析解显然是不现实的。因此，在实际应用时通常会用迭代法得到数值解：

\[ \mathbf{x}(t+\Delta t)\approx\mathbf{x}(t)+\mathbf{f}(\mathbf{x}(t),t)\Delta t \]

在迭代过程中每次沿着箭头线性地走一小段距离，经过多次迭代就可以得到解析解的一个近似，这个迭代的过程可以用下面左图中的绿色曲线表示。

从上面的描述可以发现，常微分方程描述了一个确定性的过程，而对于非确定性的过程（比如从分布中采样），则需要使用随机微分方程（SDE）进行描述。随机微分方程相比于常微分方程只是在形式上多了一个高斯噪声：

\[ \frac{\mathrm{d}\mathbf{x}}{\mathrm{d}t}=\underbrace{\mathbf{f}(\mathbf{x},t)}_{漂移系数}+\underbrace{\sigma(\mathbf{x},t)}_{扩散系数}\omega_t\quad\mathrm{or}\quad\mathrm{d}\mathbf{x}=\mathbf{f}(\mathbf{x},t)\mathrm{d}t+\sigma(\mathbf{x},t)\mathrm{d}\omega_t \]

在采样时和 ODE 类似，也可以进行迭代采样：

\[ \mathbf{x}(t+\Delta t)\approx\mathbf{x}(t)+\mathbf{f}(\mathbf{x}(t),t)\Delta t+\sigma(\mathbf{x}(t),t)\sqrt{\Delta t}\mathcal{N}(0,I) \]

而且由于采样过程中存在高斯噪声，进行多次采样会得到不同的轨迹，如下边右图中的一系列绿色折线所示。

基于 SDE 的 Score-based Models

我们在上面介绍过，通过使用多个具有不同方差的高斯噪声对分布进行扰动，可以提升概率建模的质量。那么如果将噪声的方差数量推广到无穷大，也就是使用连续的方差对分布进行扰动，就可以进一步提高概率建模的准确度。

使用 SDE 描述扰动过程

当噪声的尺度数量接近无穷大的时候，扰动的过程类似于一个连续时间内的随机过程，如下图所示，可以看出这和扩散模型的加噪过程有一些类似之处。

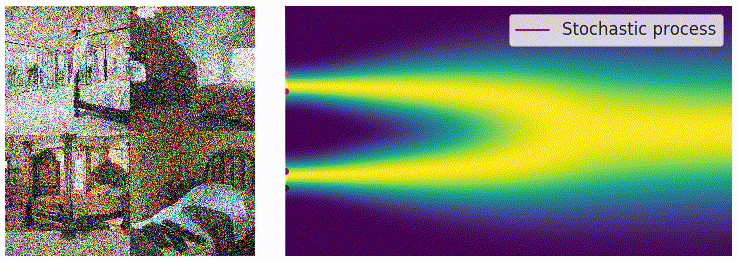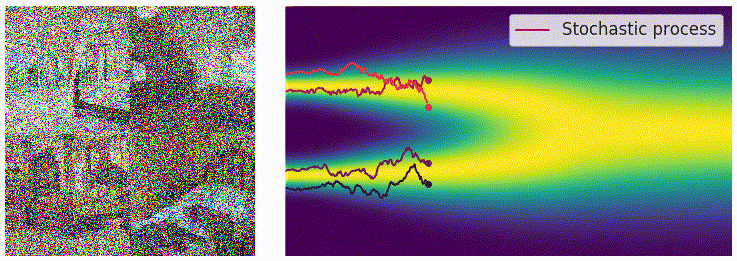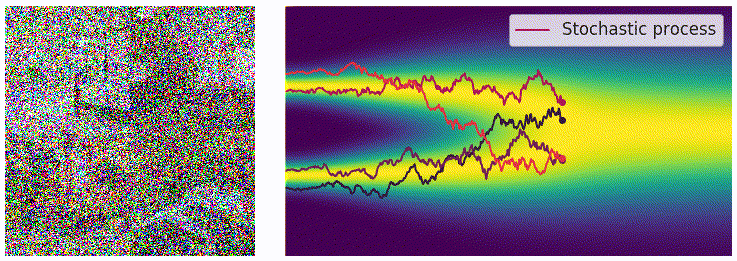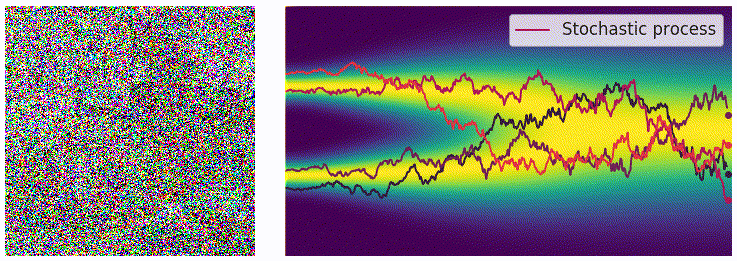
为了表示上述随机过程，可以用随机微分方程进行描述，和上面描述过的类似：

\[ \mathrm{d}\mathbf{x}=\mathbf{f}(\mathbf{x},t)\mathrm{d}t+g(t)\mathrm{d}\mathbf{w} \]

用 $p_t(\mathbf{x})$ 表示 $\mathbf{x}(t)$ 的概率密度函数，可以知道 $ p_0(\mathbf{x})=p(\mathbf{x})$ 是没有加噪时的分布，也就是真实的数据分布，经过足够多个时间步 T 的扰动， $p_T(\mathbf{x})$ 接近于先验分布 $ \pi(\mathbf{x})$。从这个角度来说，扰动的过程和扩散模型的扩散过程是一致的。就像扩散模型可以使用很多种加噪 schedule，这个扰动的随机过程可以使用的 SDE 的形式也并不是唯一的，例如：

\[ \mathrm{d}\mathbf{x}=e^t\mathrm{d}\mathbf{w} \]

就是用均值为 0、方差呈指数增长的高斯噪声对分布进行扰动。

使用反向 SDE 进行采样

在离散的过程里，可以用 annealed Langevin dynamics 进行采样，那么在这里我们的正向过程改为了使用 SDE 进行描述，逆向过程也要发生相应的变化。对于一个 SDE 来说，其逆向过程同样也是一个 SDE（推导过程见逆向方程，可以表示为：

\[ \mathrm{d}\mathbf{x}=\left[\mathbf{f}(\mathbf{x},t)-g^2(t)\color{red}{\nabla_\mathbf{x}\log p_t(\mathbf{x})}\right]\mathrm{d}t+g(t)\mathrm{d}\mathbf{w} \]

这里的 $\mathrm{d}t$ 表示的是反向的时间梯度，也就是从 t=T 到 t=0 的方向。上面的式子里有一部分我们非常熟悉，也就是红色的部分，正好就是我们上面介绍的 score function $\mathbf{s}_\theta(\mathbf{x},t)$。从这里我们可以看出，虽然从离散的形式变成了连续的形式，但是我们学习的目标都是一致的，也就是用一个网络来学习分布的 score function。得到 score function 之后我们就可以从反向 SDE 中进行采样，采样的方法也并不唯一，最简单的一种方法是 Euler-Maruyama 方法：

\[ \begin{aligned} \Delta\mathbf{x}&\leftarrow[\mathbf{f}(\mathbf{x},t)-g^2(t)\mathbf{s}_\theta(\mathbf{x},t)]\Delta t+g(t)\sqrt{|\Delta t|}\mathbf{z}_t\\ \mathbf{x}&\leftarrow\mathbf{x}+\Delta\mathbf{x}\\ t&\leftarrow t+\Delta t \end{aligned} \]

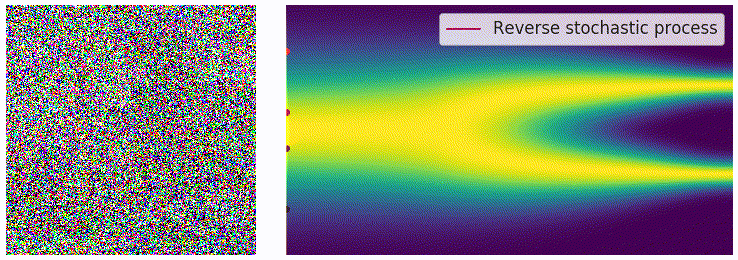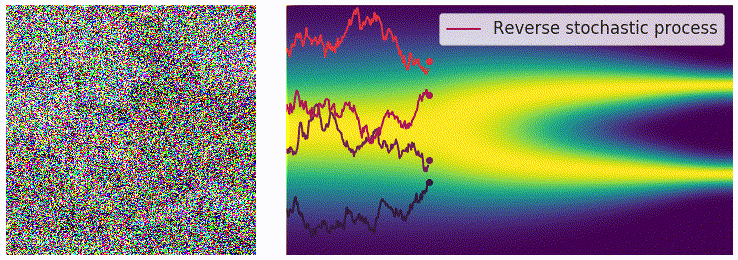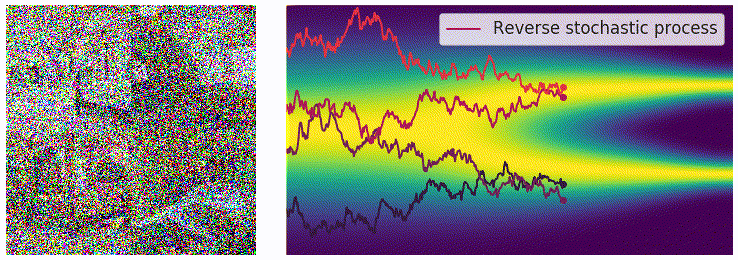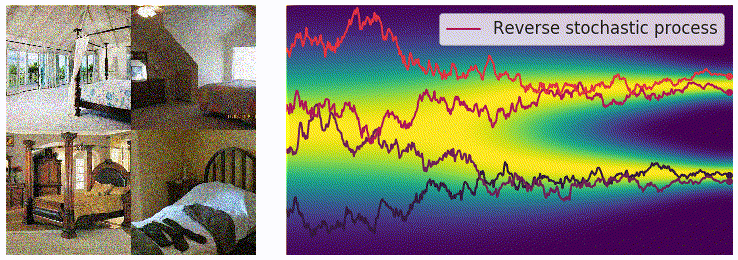
其中$ \mathbf{z}\sim\mathcal{N}(0,I)$，可以通过直接对高斯噪声采样得到。上式中的 $f(\mathbf{x},t)$ 和 $g(t)$ 都是有解析形式的， $\Delta t$ 可以选取一个比较小的值，只有 $\mathbf{s}_\theta(\mathbf{x},t)$ 是参数模型。可以从下边的动图直观感受一下采样过程：

使用 score matching 进行训练

我们知道反向 SDE 采样的过程中，需要学习的也是 score function $\mathbf{s}\theta(\mathbf{x},t)\approx\nabla\mathbf{x}\log p_t(\mathbf{x})$，那么为了对其进行估计，同样可以使用 score matching 的方式进行训练。和上面介绍的类似，优化的目标为：

\[ \mathbb{E}_{t\in\mathcal{U}(0,T)}\mathbb{E}_{p_t(\mathbf{x})}\left[\lambda(t)||\nabla_\mathbf{x}\log p_t(\mathbf{x})-\mathbf{s}_\theta(\mathbf{x},t)||_2^2\right] \]

可以看到依然是使用 L2 损失进行优化，只不过不再是简单地对所有的噪声进行求和，而是改为了计算均匀时间分布 $[0,T]$ 范围内损失的期望。另一个不同是权重的选取变为了 $\lambda(t)\propto 1/\mathbb{E}[||\nabla_{\mathbf{x}(t)}\log p(\mathbf{x}(t)|\mathbf{x}(0))||_2^2]$ 。用这种方式训练后，我们便得到了可以用于采样的 score function。

另一个比较值得讨论的点是，在离散的情况下， $\lambda(t)$ 的选取是 $\lambda(t)=\sigma_t^2$，如果我们在这里也使用类似的形式，也就是 $\lambda(t)=g^2(t)$，可以推导出 $p_0(\mathbf{x})$ 和 $p_\theta(\mathbf{x})$ 之间的 KL 散度和上述损失之间的关系：

\[ \mathrm{KL}(p_0(\mathbf{x})||p_\theta(\mathbf{x}))\le\frac{T}{2}\mathbb{E}_{t\in\mathcal{U}(0,T)}\mathbb{E}_{p_t(\mathbf{x})}\left[\lambda(t)||\nabla_\mathbf{x}\log p_t(\mathbf{x})-\mathbf{s}_\theta(\mathbf{x},t)||_2^2\right]+\mathrm{KL}(p_T||\pi) \]

这里的 $\lambda(t)=g^2(t) $ 被称作 likelihood weighting function，通过使用这个加权函数，可以学习到非常好的分布。从这个角度来说，连续的表示方式和离散的表示方式依然是统一的。