Swin-Transformer

Apr 25, 2024
1 views
Computer Vision
# CV # transformer

前言

首先看论文题目。Swin Transformer： Hierarchical Vision Transformer using Shifted Windows。即：Swin Transformer是一个用了移动窗口的层级式Vision Transformer

所以Swin来自于 Shifted Windows ， 它能够使Vision Transformer像卷积神经网络一样，做层级式的特征提取，这样提取出来的特征具有多尺度的概念 ，这也是 Swin Transformer这篇论文的主要贡献。

标准的Transformer直接用到视觉领域有一些挑战，即：

  • 多尺度问题：比如一张图片里的各种物体尺度不统一，NLP中没有这个问题；

  • 分辨率太大：如果将图片的每一个像素值当作一个token直接输入Transformer，计算量太大，不利于在多种机器视觉任务中的应用。
    基于这两点，本文提出了 hierarchical Transformer，通过移动窗口来学习特征。

  • 移动窗口学习，即只在滑动窗口内部计算自注意力，所以称为W-MSA（Window Multi-Self-Attention）。

  • W-MSA大大降低了降低了计算复杂度。同时通过Shiting（移动）的操作可以使相邻的两个窗口之间进行交互，也因此上下层之间有了cross-window connection，从而变相达到了全局建模的能力。
  • 分层结构使得模型能够灵活处理不同尺度的图片，并且计算复杂度与图像大小呈线性关系，这样模型就可以处理更大分辨率的图片（为作者后面提出的Swin V2铺平了道路）。

Swin-Transformer 对比 VIT

Vision Transformer：进行MSA（多头注意力）计算时，任何一个patch都要与其他所有的patch都进行attention计算，计算量与图片的大小成平方增长。
Swin Transformer：采用了W-MSA，只对window内部计算MSA，当图片大小增大时，计算量仅仅是呈线性增加。

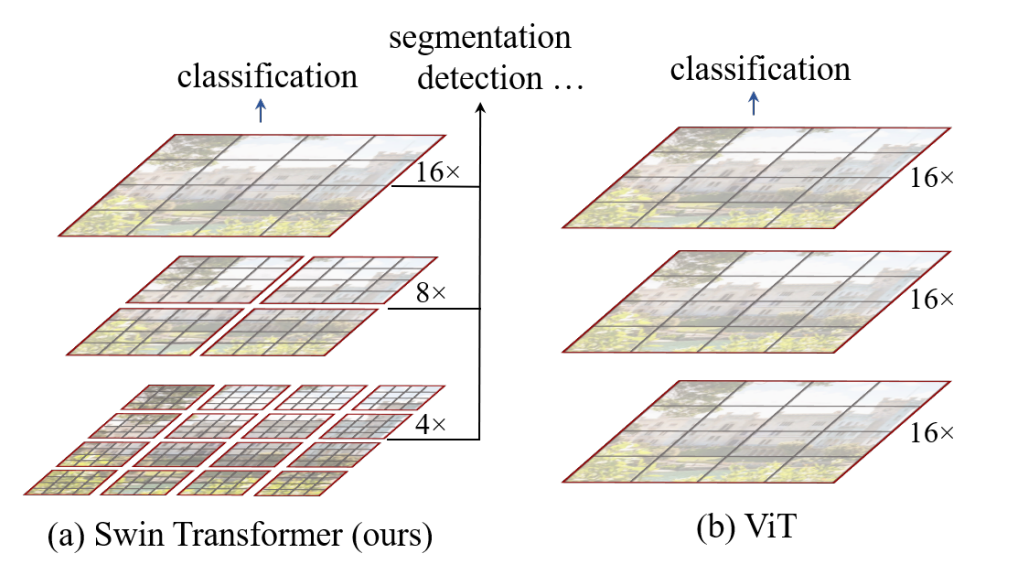
image

可以看出主要区别有两个：

  1. 层次化构建方法（Hierarchical feature maps） ：Swin Transformer使用了类似卷积神经网络中的层次化构建方法。
  2. 使用W-MSA ，好处有两点：

方法部分

模型结构

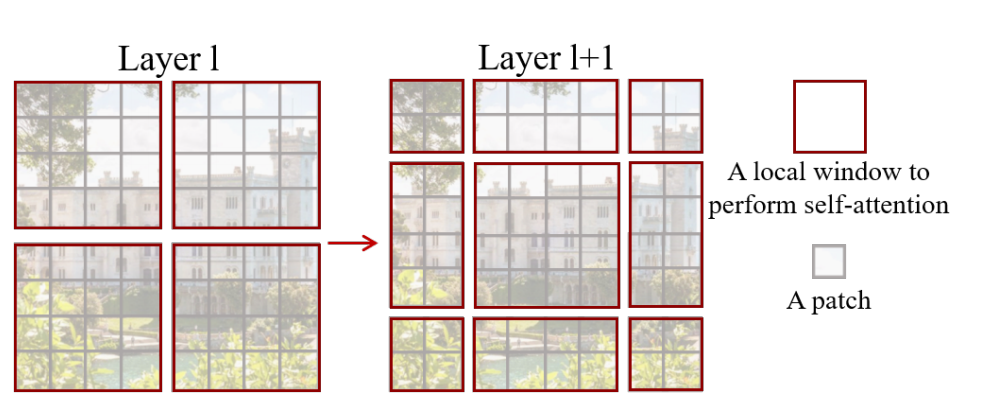
原论文中给出的关于Swin Transformer（Swin-T）网络的架构图如下：

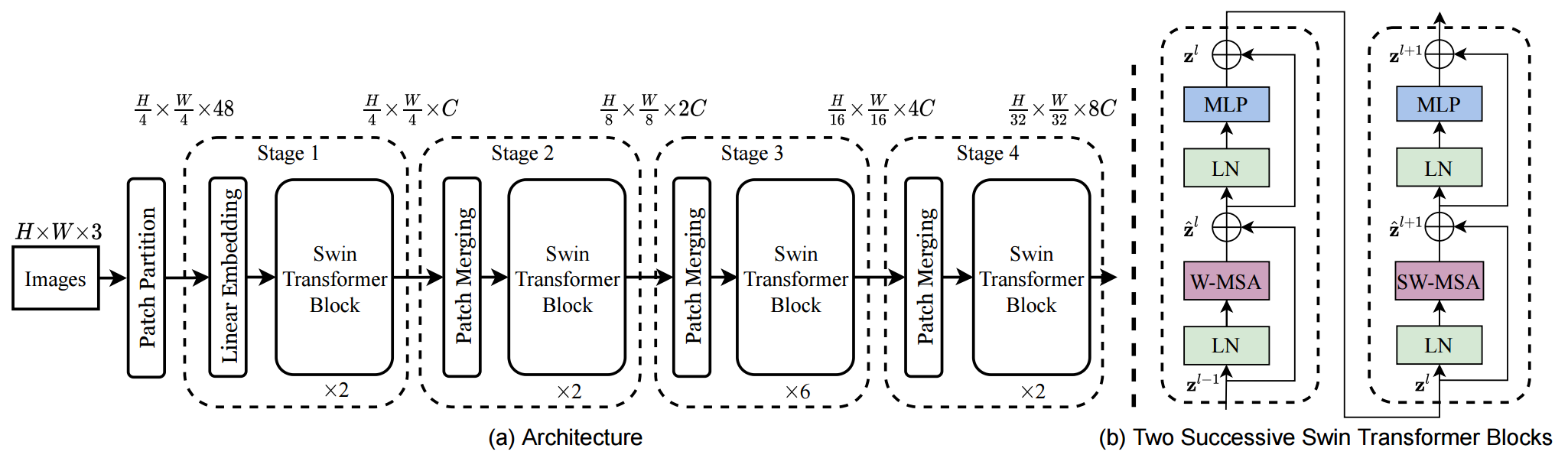
image

前向过程：

  1. Patch Partition层：类似ViT一样将图片分割成一个个4*4大小的patch（[224,224,3]—>[56,56,48]）
  2. Linear Embeding层：将每个像素的channel数调整为C，并对每个channel做一次Layer Norm。（[56,56,48]—>[56,56,96]）
  3. 将每49个patch划分为一个窗口，后续只在窗口内进行计算。
  4. 通过四个Stage构建不同大小的特征图。其中后三个stage都是先通过一个Patch Merging层进行2倍的下采样。（[56,56,96]—>[28,28,192]—>[14,14,384]—>[7,7,768]）
  5. 每个stage中，重复堆叠Swin Transformer Block偶数次（结构见上图右侧，分别使用W-MSA和SW-MSA，两个结构成对出现）。
  6. 如果是分类任务，后面还会接上一个Layer Norm层、全局池化层以及全连接层得到最终输出。[7,7,768]—>[1,768]—>[1,num_class]（也就是做序列的全局平均，类似CNN的做法，而不是加上CLS做分类）
    看完整个前向过程之后，就会发现 Swin Transformer 有四个 stage，还有类似于池化的 patch merging 操作，自注意力还是在小窗口之内做的，以及最后还用的是全局平均池化 。所以可以说 Swin Transformer是披着Transformer皮的卷积神经网络，将二者进行了完美的结合。

接下来，在分别对Patch Merging、W-MSA、SW-MSA以及使用到的相对位置偏置（relative position bias）进行详解。

图片预处理：分块和降维 (Patch Partition)

Swin Transformer 首先把\(x\in H\times W \times 3\) 的图片，变成一个 \(x_p\in N\times(P^2\cdot C)\) 的2维的image patches。它可以看做是一系列的展平的2D块的序列，这个序列中一共有 \(N=HW/P^2\)个展平的2D块，每个块的维度是 \(P^2\cdot 3\) 。其中 \(P\) 是块大小。

在 Swin Transformer 中，块的大小 \(P=4\) ，所以得到的 \(x_p\in N×48\) ，这里的 \(N=HW/16=\frac{H}{4}\times\frac{W}{4}\) 。

所以经过了这一步的分块操作，一张\(x\in H\times W \times 3\) 的图片就变成了 \(\frac{H}{4}\times\frac{W}{4}\times 48\) 的张量，可以理解成是 \(\frac{H}{4}\times\frac{W}{4}\) 个图片块，每个块是一个 48 维的 token。

线性变换 (Linear Embedding)

现在得到的向量维度是： \(\frac{H}{4}\times\frac{W}{4}\times 48\) ，还需要做一步叫做Linear Embedding的步骤，对每个向量都做一个线性变换（即全连接层），变换后的维度为 \(C\) ，这里我们称其为 Linear Embedding。这一步之后得到的张量维度是： \(\frac{H}{4}\times\frac{W}{4}\times C\) 。

Stage1: Swin Transformer Block

接下来 \(\frac{H}{4}\times\frac{W}{4}\times 48\) 这个张量进入2个连续的 Swin Transformer Block 中，这被称作 Stage 1，在整个的 Stage 1 里面 token 的数量一直维持 \(\frac{H}{4}\times\frac{W}{4}\) 不变。

Swin Transformer Block 具体是如何操作的呢？

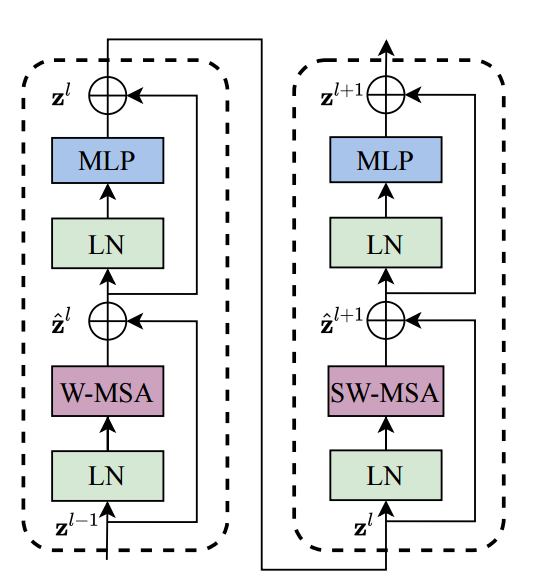
image

Swin Transformer Block 的结构如上图所示。上图是2个连续的 Swin Transformer Block。其中一个 Swin Transformer Block 由一个带两层 MLP 的 Shifted Window-based MSA 组成，另一个 Swin Transformer Block 由一个带两层 MLP 的 Window-based MSA 组成。在每个 MSA 模块和每个 MLP 之前使用 LayerNorm(LN) 层，并在每个 MSA 和 MLP之后使用残差连接。

可以看到 Swin Transformer Block 和 ViT Block 的区别就在于将 ViT 的多头注意力机制 MSA 替换为了 Shifted Window-based MSA 和 Window-based MSA。

Stage1: Swin Transformer Block：Window-based MSA

标准 ViT 的多头注意力机制 MSA 采用的是全局自注意力机制，即：计算每个 token 和所有其他 token 的 attention map。全局自注意力机制的计算复杂度是 \(O(N^2d)\) ，其中， \(N\) 是 token的数量， \(d\) 是 Embedding dimension。全局自注意力机制的计算复杂度与序列长度 \(N\) 成平方关系。当图片分辨率较高或是密集预测任务中计算量会过大。

Window-based MSA 不同于普通的 MSA，它在一个个 window 里面去计算 self-attention。假设每个 window 里面包括 $M×M $个 image patches，则 Window-based MSA 和普通的 MSA 的计算量分别为：

\[ Ω(MSA)=4ℎwC^2+2(ℎw)^2C,\\ Ω(W-MSA)=4ℎwC^2+2M^2ℎwC, \]

由于 Window 的 patch 数量 \(M\) 远小于图片patch数量 \(ℎw\) ，Window-based MSA 的计算量与序列长度 \(N=hw\) 成线性关系。

Stage1: Swin Transformer Block：Shifted Window-based MSA

与W-MSA不同的地方在于这个模块存在窗口滑动，所以叫做shifted window。滑动距离是window_size//2，方向是向右和向下。
  滑动窗口是为了解决W-MSA计算attention时，窗口与窗口之间无法进行信息传递的问题。如下图所示，左侧是网络第L层使用的W-MSA模块，右侧是第L+1层使用SW-MSA模块。对比可以发现，窗口（Windows）发生了偏移。

比如在L+1层特征图上，对于第一行第2列的2x4的窗口，它能够使第L层的第一排的两个窗口信息进行交流。再比如，第二行第二列的4x4的窗口，他能够使第L层的四个窗口信息进行交流，其他同理。

image

但是引入 Shifted Window 会带来另一个问题就是会造成 window 数发生改变，而且有的 window 大，有的 window 小

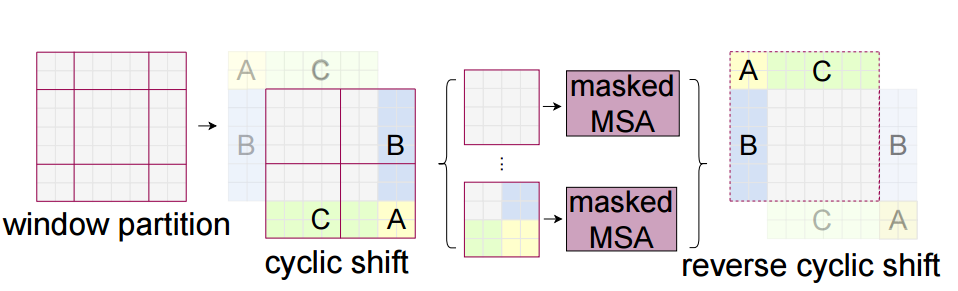
image

一种简单的解决办法是把所有 window 都做 padding 操作，使之达到相同的大小。但是这会因为 window 数量的增加 (从$ ⌈\frac{h}{M}⌉×⌈\frac{w}{M}⌉$ 增加到 $ (⌈\frac{h}{M}⌉+1)×（⌈\frac{w}{M}⌉+1）$而增加计算量。所以作者在这里提出了一种更加高效的 batch computation 计算方法，通过 cycle shift 的方法，合并小的 windows，仔细看上图，将 A,B,C 这3个小的 windows 进行循环移位，使之合并小的 windows。

经过了 cycle shift 的方法，一个 window 可能会包括来自不同 window 的内容。比如图中右下角的 window，来自4个不同的 sub-window。因此，要采用 masked MSA 机制将 self-attention 的计算限制在每个子窗口内。最后通过 reverse cycle shift 的方法将每个 window 的 self-attention 结果返回。

这里进行下简单的图解，下图代表 cycle shift 的过程，这9个 window 通过移位从左边移动到右侧的位置。

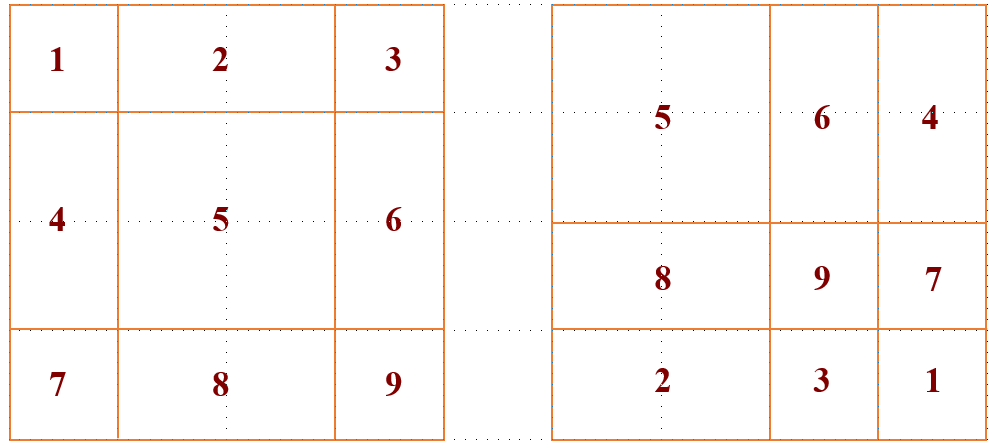
image

这样再按照之前的 window 划分，就能够得到 window 5 的attention 的结果了。但是这样操作会使得 window 6 和 4 的 attention 混在一起，window 1,3,7 和 9 的 attention 混在一起。所以需要采用 masked MSA 机制将 self-attention 的计算限制在每个子窗口内。具体怎么做呢？

按照 Swin Transformer 的代码实现 (下面会有讲解)，还是做正常的 self-attention (在 window_size 上做)，之后要进行一次 mask 操作，把不需要的 attention 值给它置为0。

  • 例1：比如右上角这个 window，如下图所示。它由4个 patch 组成，所以应该计算出的 attention map是4×4的。但是6和4是2个不同的 sub-window，我们又不想让它们的 attention 发生交叠。所以我们希望的 attention map 应该是下图这个样子。
  • 例2：比如右下角这个 window，如下图9所示。它由4个 patch 组成，所以应该计算出的 attention map是4×4的。但是1，3，7和9是4个不同的 sub-window，我们又不想让它们的 attention 发生交叠。所以我们希望的 mask 应该是这个样子。

Stage 2/3/4

Stage 2 的输入是维度是 \(\frac{H}{4}\times\frac{W}{4}\times C\) 的张量。从 Stage 2 到 Stage 4 的每个 stage 的初始阶段都会先做一步 Patch Merging 操作，Patch Merging 操作的目的是为了减少 tokens 的数量，它会把相邻的 2×2 个 tokens 给合并到一起，得到的 token 的维度是 \(4C\) 。Patch Merging 操作再通过一个\(1\times 1\)的卷积把维度降为 \(2C\) 。至此，维度是 \(\frac{H}{4}\times\frac{W}{4}\times C\) 的张量经过Patch Merging 操作变成了维度是 \(\frac{H}{8}\times\frac{W}{8}\times 2C\) 的张量。

同理，Stage 3 的Patch Merging 操作会把维度是\(\frac{H}{8}\times\frac{W}{8}\times 2C\) 的张量变成维度是 \(\frac{H}{16}\times\frac{W}{16}\times 4C\) 的张量。Stage 4 的Patch Merging 操作会把维度是 \(\frac{H}{16}\times\frac{W}{16}\times 4C\) 的张量变成维度是 \(\frac{H}{32}\times\frac{W}{32}\times 8C\) 的张量。

每个 Stage 都会改变张量的维度，形成一种层次化的表征。因此，这种层次化的表征可以方便地替换为各种视觉任务的骨干网络。

相对位置编码

注意 Swin Transformer 的位置编码是加在 attention 矩阵上的，attention 是个四维张量，它的维度是：

(num_windows,num_heads,windows_sizewindows_size,windows_sizewindows_size)

具体操作为

\[ Attention(Q, K, V ) = SoftMax(QK^T/√d + B)V \]

下面具体讲解什么是Relative Position Bias（假设特征图大小为2×2）

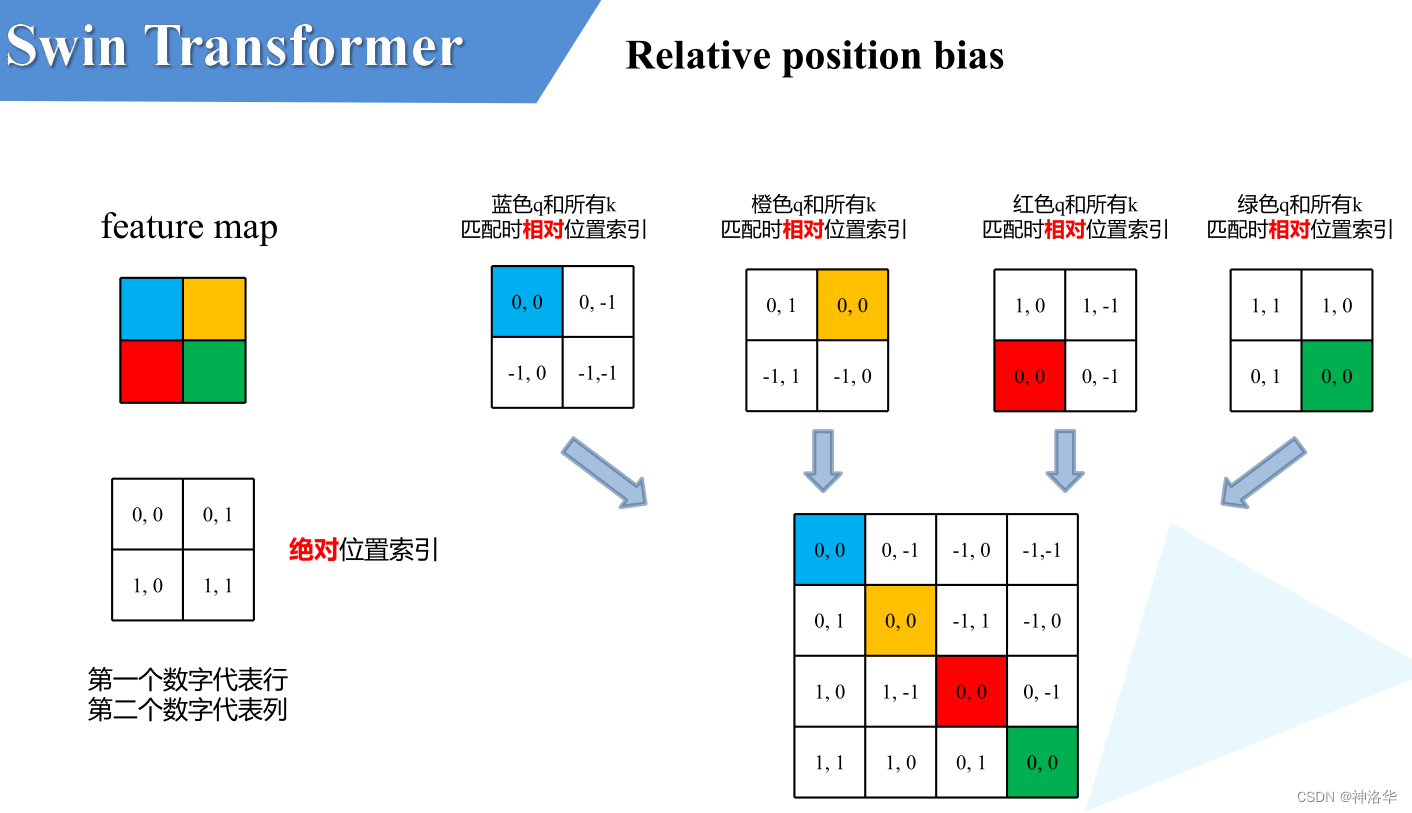
image

  1. 计算相对位置索引：比如蓝色像素，在蓝色像素使用q与所有像素k进行匹配过程中，是以蓝色像素为参考点。然后用蓝色像素的绝对位置索引与其他位置索引进行相减，就得到其他位置相对蓝色像素的相对位置索引，同理可以得到其他位置相对蓝色像素的相对位置索引矩阵（第一排四个位置矩阵）。
  2. 展平拼接：将每个相对位置索引矩阵按行展平，并拼接在一起可以得到第二排的这个4x4矩阵
  3. 索引转换为一维：在源码中作者为了方便把二维索引给转成了一维索引。
  4. 取出相对位置偏置参数。真正使用到的可训练参数B 是保存在relative position bias table表里的，其长度是等于 \((2M-1) \times (2M-1)\)。相对位置偏置参数B，是根据相对位置索引来查relative position bias table表得到的，如下图所示。
    为啥表长是 \((2M-1) \times (2M-1)\)？考虑两个极端位置，（0,0）能取到的相对位置极值为（-1，-1），（-1，-1）能取到的极值是（1，1），即行和列都能取到（2M-1）个数。考虑到所有的排列组合，表的长度就是$( 2 M − 1 ) × ( 2 M − 1 ) $

Swin Transformer 的结构

Swin Transformer 分为 Swin-T，Swin-S，Swin-B，Swin-L 这四种结构。使用的 window 的大小统一为 \(M=7\) ，每个 head 的embedding dimension 都是 32，每个 stage 的层数如下：

  • Swin-T：\(C=96\)  ，layer number：\(\{2,2,6,2\}\)
  • Swin-T：\(C=96\)  ，layer number：\(\{2,2,18,2\}\)
  • Swin-T：\(C=128\)  ，layer number：\(\{2,2,18,2\}\)
  • Swin-T：\(C=192\)  ，layer number：\(\{2,2,18,2\}\)

Experiments：

图像分类：

数据集：ImageNet

(a)表是直接在 ImageNet-1k 上训练，(b)表是先在 ImageNet-22k 上预训练，再在 ImageNet-1k 上微调。

对标 88M 参数的 DeiT-B 模型，它在 ImageNet-1k 上训练的结果是83.1% Top1 Accuracy，Swin-B 模型的参数是80M，它在 ImageNet-1k 上训练的结果是83.5% Top1 Accuracy，优于DeiT-B 模型。

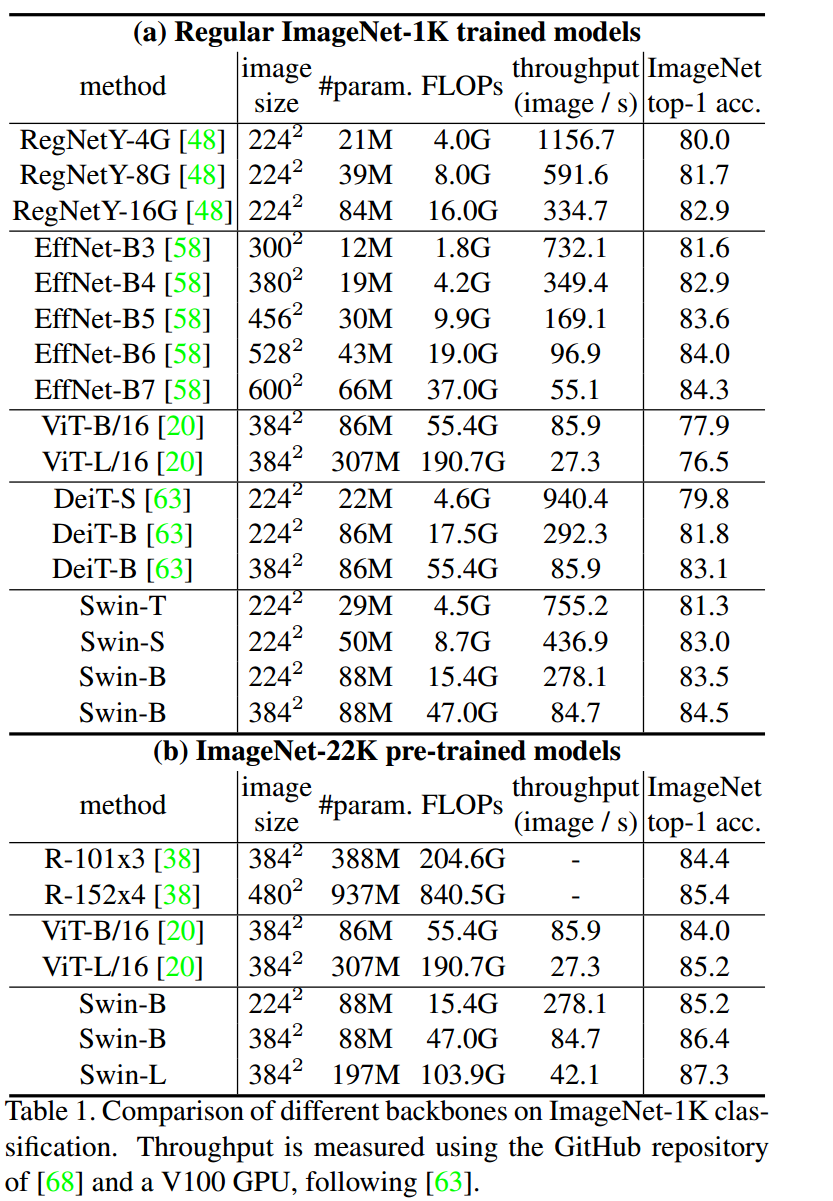
image

图像分类上比 ViT、DeiT等 Transformer 类型的网络效果更好，但是比不过 CNN 类型的EfficientNet，猜测 Swin Transformer 还是更加适用于更加复杂、尺度变化更多的任务。

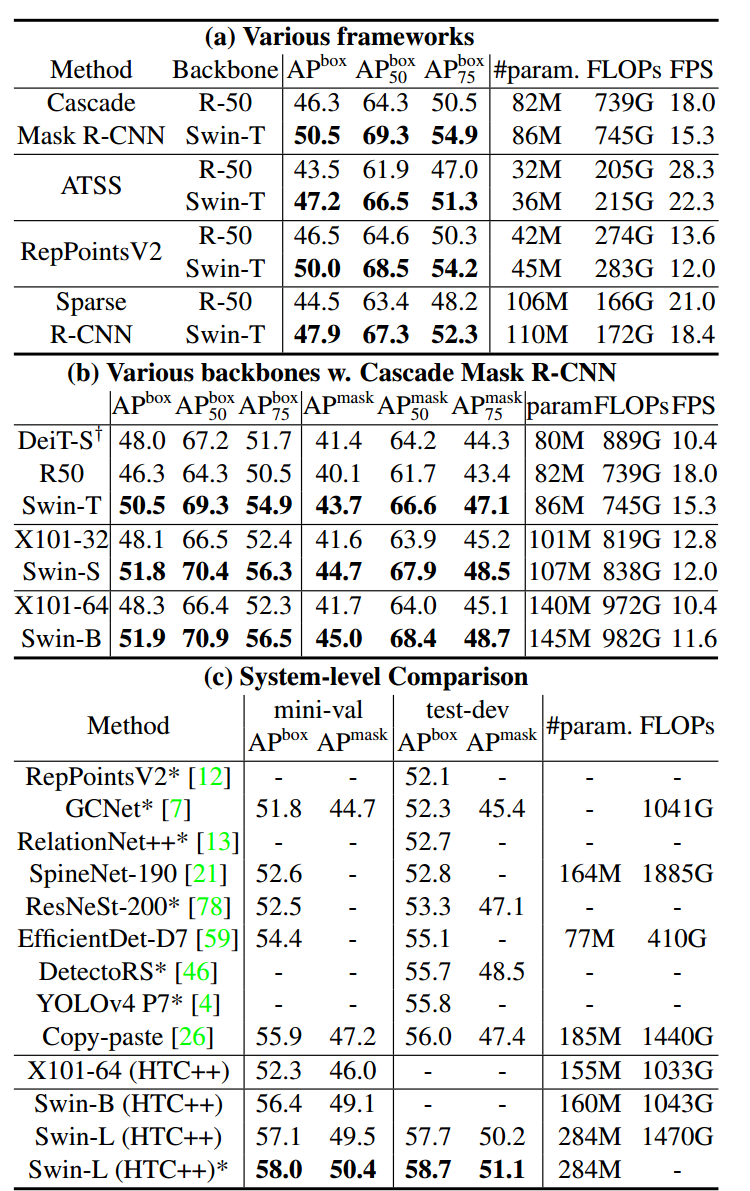
2 目标检测：

数据集：COCO 2017 (118k Training, 5k validation, 20k test)

(a) 表是在 Cascade Mask R-CNN, ATSS, RepPoints v2, 和 Sparse RCNN 上对比 Swin-T 和 ResNet-50 作为 Backbone 的性能。

(b) 表是使用 Cascade Mask R-CNN 模型的不同 Backbone 的性能对比。

(c) 表是整体的目标检测系统的对比，在 COCO test-dev 上达到了 58.7 box AP 和 51.1 mask AP。

image

语义分割：

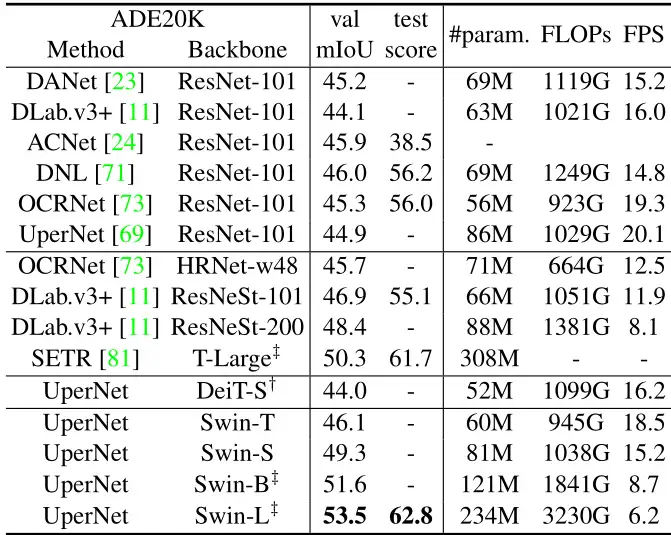
数据集：ADE20K (20k Training, 2k validation, 3k test)

下图13列出了不同方法/Backbone的mIoU、模型大小(#param)、FLOPs和FPS。从这些结果可以看出，Swin-S 比具有相似计算成本的 DeiT-S 高出+5.3 mIoU (49.3 vs . 44.0)。也比ResNet-101 高+4.4 mIoU，比 ResNeSt-101 高 +2.4 mIoU。

image