旋转式位置编码(ROPE)
原始的Sinusoidal位置编码总的感觉是一种“想要成为相对位置编码的绝对位置编码”。一般来说,绝对位置编码具有实现简单、计算速度快等优点,而相对位置编码则直接地体现了相对位置信号,跟我们的直观理解吻合,实际性能往往也更好。由此可见,如果可以通过绝对位置编码的方式实现相对位置编码,那么就是“集各家之所长”、“鱼与熊掌兼得”了。Sinusoidal位置编码隐约做到了这一点,但并不够好。
本文将会介绍我们自研的Rotary Transformer(RoFormer)模型,它的主要改动是应用了笔者构思的“旋转式位置编码(Rotary Position Embedding,RoPE)”,这是一种配合Attention机制能达到“绝对位置编码的方式实现相对位置编码”的设计。而也正因为这种设计,它还是目前唯一一种可用于线性Attention的相对位置编码。
RoFormer:https://github.com/ZhuiyiTechnology/roformer
基本思路
这里简要介绍过RoPE:Transformer位置编码,当时称之为“融合式”,本文则更加详细地介绍它的来源与性质。
在RoPE中,我们的出发点就是“通过绝对位置编码的方式实现相对位置编码”,这样做既有理论上的优雅之处,也有实践上的实用之处,比如它可以拓展到线性Attention中就是主要因为这一点。
为了达到这个目的,我们假设通过下述运算来给 \(𝑞,𝑘\) 添加绝对位置信息:
也就是说,我们分别为\(𝑞,𝑘\) 设计操作\(\boldsymbol{f}(\cdot, m),\boldsymbol{f}(\cdot, n)\),使得经过该操作后,\(\tilde{\boldsymbol{q}}_m,\tilde{\boldsymbol{k}}_n\) 就带有了位置 \(𝑚,𝑛\) 的绝对位置信息。Attention的核心运算是内积,所以我们希望的内积的结果带有相对位置信息,因此假设存在恒等关系:
所以我们要求出该恒等式的一个(尽可能简单的)解。求解过程还需要一些初始条件,显然我们可以合理地设\(\boldsymbol{f}(\boldsymbol{q}, 0)=\boldsymbol{q}\) 和 \(\boldsymbol{f}(\boldsymbol{k}, 0)=\boldsymbol{k}\)。
求解过程
同上一篇思路一样,我们先考虑二维情形,然后借助复数来求解。在复数中有\(\langle\boldsymbol{q},\boldsymbol{k}\rangle=\text{Re}[\boldsymbol{q}\boldsymbol{k}^*]\),\(Re[]\) 代表复数的实部,所以我们有
简单起见,我们假设存在复数 \(𝑔(𝑞,𝑘,𝑚−𝑛)\),使得 \(\boldsymbol{f}(\boldsymbol{q}, m)\boldsymbol{f}^*(\boldsymbol{k}, n) = \boldsymbol{g}(\boldsymbol{q},\boldsymbol{k},m-n)\),然后我们用复数的指数形式,设
那么代入方程后就得到方程组
对于第一个方程,代入 \(𝑚=𝑛\) 得到
最后一个等号源于初始条件\(\boldsymbol{f}(\boldsymbol{q}, 0)=\boldsymbol{q}\) 和 \(\boldsymbol{f}(\boldsymbol{k}, 0)=\boldsymbol{k}\)。所以现在我们可以很简单地设\(R_f (\boldsymbol{q}, m)=\Vert \boldsymbol{q}\Vert, R_f (\boldsymbol{k}, m)=\Vert \boldsymbol{k}\Vert\),即它不依赖于 \(𝑚\)。至于第二个方程,同样代入 \(𝑚=𝑛\) 得到
这里的 \(\Theta (\boldsymbol{q}),\Theta (\boldsymbol{k})\) 是 \(𝑞,𝑘\) 本身的幅角,最后一个等号同样源于初始条件。根据上式得到 \(\Theta_f (\boldsymbol{q}, m) - \Theta (\boldsymbol{q}) = \Theta_f (\boldsymbol{k}, m) - \Theta (\boldsymbol{k})\),所以 \(\Theta_f (\boldsymbol{q}, m) - \Theta (\boldsymbol{q})\) 应该是一个只与 \(𝑚\) 相关、跟 \(𝑞\) 无关的函数,记为 \(𝜑(𝑚)\),即 \(\Theta_f (\boldsymbol{q}, m) = \Theta (\boldsymbol{q}) + \varphi(m)\)。接着代入 \(𝑛=𝑚−1\),整理得到
即\(\{𝜑(𝑚)\}\) 是等差数列,设右端为 \(𝜃 \) ,那么就解得 \(\varphi(m)=m\theta\) 。
编码形式
综上,我们得到二维情况下用复数表示的RoPE:
根据复数乘法的几何意义,该变换实际上对应着向量的旋转,所以我们称之为“旋转式位置编码”,它还可以写成矩阵形式:
由于内积满足线性叠加性,因此任意偶数维的RoPE,我们都可以表示为二维情形的拼接,即
也就是说,给位置为 \(𝑚\) 的向量 \(𝑞\) 乘上矩阵\(\boldsymbol{\mathcal{R}}_m\)、位置为 \(𝑛\) 的向量 \(𝑘\) 乘上矩阵 \(\boldsymbol{\mathcal{R}}_n\),用变换后的 \(\boldsymbol{Q},\boldsymbol{K}\) 序列做Attention,那么Attention就自动包含相对位置信息了,因为成立恒等式:
值得指出的是,\(\boldsymbol{\mathcal{R}}_m\) 是一个正交矩阵,它不会改变向量的模长,因此通常来说它不会改变原模型的稳定性。
由于\(\boldsymbol{\mathcal{R}}_m\) 的稀疏性,所以直接用矩阵乘法来实现会很浪费算力,推荐通过下述方式来实现RoPE:
其中\(\otimes\) 是逐位对应相乘,即Numpy、Tensorflow等计算框架中的\(∗ \)运算。从这个实现也可以看到,RoPE可以视为是乘性位置编码的变体。
远程衰减
可以看到,RoPE形式上和Sinusoidal位置编码有点相似,只不过Sinusoidal位置编码是加性的,而RoPE可以视为乘性的。在\(𝜃_𝑖\) 的选择上,我们同样沿用了Sinusoidal位置编码的方案,即 \(\theta_i = 10000^{-2i/d}\),它可以带来一定的远程衰减性。
具体证明如下:将 \(𝑞,𝑘\) 两两分组后,它们加上RoPE后的内积可以用复数乘法表示为
记 \(h_i = \boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^*, S_j = \sum\limits_{i=0}^{j-1} e^{\text{i}(m-n)\theta_i}\),并约定 \(h_{d/2}=0,S_0=0\),那么由 Abel变换(分部求和法)可以得到:
所以
因此我们可以考察 \(\frac{1}{d/2}\sum\limits_{i=1}^{d/2} |S_i|\) 随着相对距离的变化情况来作为衰减性的体现,Mathematica代码如下:
d = 128;
\[Theta][t_] = 10000^(-2*t/d);
f[m_] = Sum[
Norm[Sum[Exp[I*m*\[Theta][i]], {i, 0, j}]], {j, 0, d/2 - 1}]/(d/2);
Plot[f[m], {m, 0, 256}, AxesLabel -> {相对距离, 相对大小}]结果如下图:
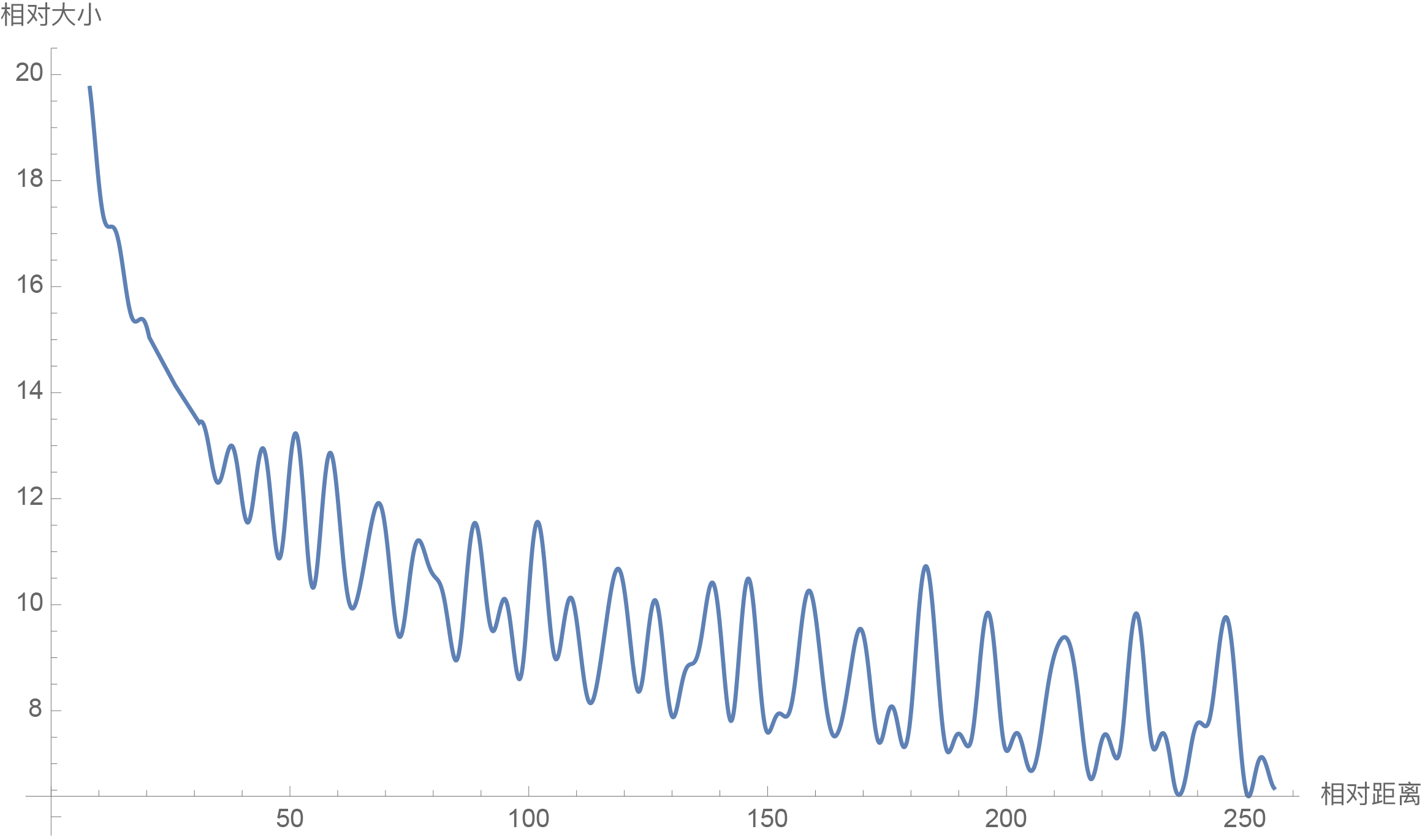
从图中我们可以可以看到随着相对距离的变大,内积结果有衰减趋势的出现。因此,选择\(\theta_i = 10000^{-2i/d}\),确实能带来一定的远程衰减性。当然,同上一篇文章说的一样,能带来远程衰减性的不止这个选择,几乎任意的光滑单调函数都可以,这里只是沿用了已有的选择而已。笔者还试过以 \(\theta_i = 10000^{-2i/d}\) 为初始化,将\(𝜃_𝑖\)视为可训练参数,然后训练一段时间后发现 \(θ_i\) 并没有显著更新,因此干脆就直接固定\(\theta_i = 10000^{-2i/d}\)了。
线性场景
最后,我们指出,RoPE是目前唯一一种可以用于线性Attention的相对位置编码。这是因为其他的相对位置编码,都是直接基于Attention矩阵进行操作的,但是线性Attention并没有事先算出Attention矩阵,因此也就不存在操作Attention矩阵的做法,所以其他的方案无法应用到线性Attention中。而对于RoPE来说,它是用绝对位置编码的方式来实现相对位置编码,不需要操作Attention矩阵,因此有了应用到线性Attention的可能性。
关于线性Attention的介绍,这里不再重复,有需要的读者请参考《线性Attention的探索:Attention必须有个Softmax吗?》。线性Attention的常见形式是:
其中 \(𝜙,𝜑\) 是值域非负的激活函数。可以看到,线性Attention也是基于内积的,所以很自然的想法是可以将RoPE插入到内积中:
但这样存在的问题是,内积 \([\boldsymbol{\mathcal{R}}_i\phi(\boldsymbol{q}_i)]^{\top} [\boldsymbol{\mathcal{R}}_j\varphi(\boldsymbol{k}_j)]\) 可能为负数,因此它不再是常规的概率注意力,而且分母有为0的风险,可能会带来优化上的不稳定。考虑到 \(\boldsymbol{\mathcal{R}}_i,\boldsymbol{\mathcal{R}}_j\) 都是正交矩阵,它不改变向量的模长,因此我们可以抛弃常规的概率归一化要求,使用如下运算作为一种新的线性Attention:
也就是说,RoPE只插入分子中,而分母则不改变,这样的注意力不再是基于概率的(注意力矩阵不再满足非负归一性),但它某种意义上来说也是一个归一化方案,而且也没有证据表明非概率式的注意力就不好(比如 Nyströmformer 也算是没有严格依据概率分布的方式构建注意力),所以我们将它作为候选方案之一进行实验,而我们初步的实验结果显示这样的线性Attention也是有效的。
此外,笔者在《线性Attention的探索:Attention必须有个Softmax吗?》中还提出过另外一种线性Attention方案:\(\text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j) = 1 + \left( \frac{\boldsymbol{q}_i}{\Vert \boldsymbol{q}_i\Vert}\right)^{\top}\left(\frac{\boldsymbol{k}_j}{\Vert \boldsymbol{k}_j\Vert}\right)\),它不依赖于值域的非负性,而RoPE也不改变模长,因此RoPE可以直接应用于此类线性Attention,并且不改变它的概率意义。
模型开源
RoFormer的第一版模型,我们已经完成训练并开源到了Github中:
RoFormer:https://github.com/ZhuiyiTechnology/roformer
简单来说,RoFormer是一个绝对位置编码替换为RoPE的WoBERT模型,它跟其他模型的结构对比如下:
在预训练上,我们以WoBERT Plus为基础,采用了多个长度和batch size交替训练的方式,让模型能提前适应不同的训练场景:
从表格还可以看到,增大序列长度,预训练的准确率反而有所提升,这侧面体现了RoFormer长文本语义的处理效果,也体现了RoPE具有良好的外推能力。在短文本任务上,RoFormer与WoBERT的表现类似,RoFormer的主要特点是可以直接处理任意长的文本。下面是我们在 CAIL2019-SCM 任务上的实验结果:
其中--后面的参数是微调时截断的maxlen,可以看到RoFormer确实能较好地处理长文本语义,至于设备要求,在24G显存的卡上跑maxlen=1024,batch_size可以跑到8以上。目前中文任务中笔者也就找到这个任务比较适合作为长文本能力的测试,所以长文本方面只测了这个任务,欢迎读者进行测试或推荐其他评测任务。
当然,尽管理论上RoFormer能处理任意长度的序列,但目前RoFormer还是具有平方复杂度的,我们也正在训练基于线性Attention的RoFormer模型,实验完成后也会开源放出,请大家期待。
在LLAMA中的实现
# 生成旋转矩阵
def precompute_freqs_cis(dim: int, seq_len: int, theta: float = 10000.0):
# 计算词向量元素两两分组之后,每组元素对应的旋转角度\theta_i
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
# 生成 token 序列索引 t = [0, 1,..., seq_len-1]
t = torch.arange(seq_len, device=freqs.device)
# freqs.shape = [seq_len, dim // 2]
freqs = torch.outer(t, freqs).float() # 计算m * \theta
# 计算结果是个复数向量
# 假设 freqs = [x, y]
# 则 freqs_cis = [cos(x) + sin(x)i, cos(y) + sin(y)i]
freqs_cis = torch.polar(torch.ones_like(freqs), freqs)
return freqs_cis
# 旋转位置编码计算
def apply_rotary_emb(
xq: torch.Tensor,
xk: torch.Tensor,
freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
# xq.shape = [batch_size, seq_len, dim]
# xq_.shape = [batch_size, seq_len, dim // 2, 2]
xq_ = xq.float().reshape(*xq.shape[:-1], -1, 2)
xk_ = xk.float().reshape(*xk.shape[:-1], -1, 2)
# 转为复数域
xq_ = torch.view_as_complex(xq_)
xk_ = torch.view_as_complex(xk_)
# 应用旋转操作,然后将结果转回实数域
# xq_out.shape = [batch_size, seq_len, dim]
xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(2)
xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(2)
return xq_out.type_as(xq), xk_out.type_as(xk)
class Attention(nn.Module):
def __init__(self, args: ModelArgs):
super().__init__()
self.wq = Linear(...)
self.wk = Linear(...)
self.wv = Linear(...)
self.freqs_cis = precompute_freqs_cis(dim, max_seq_len * 2)
def forward(self, x: torch.Tensor):
bsz, seqlen, _ = x.shape
xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)
xq = xq.view(batch_size, seq_len, dim)
xk = xk.view(batch_size, seq_len, dim)
xv = xv.view(batch_size, seq_len, dim)
# attention 操作之前,应用旋转位置编码
xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)
# scores.shape = (bs, seqlen, seqlen)
scores = torch.matmul(xq, xk.transpose(1, 2)) / math.sqrt(dim)
scores = F.softmax(scores.float(), dim=-1)
output = torch.matmul(scores, xv) # (batch_size, seq_len, dim)
# ......这里举一个例子,假设 batch_size=10, seq_len=3, d=8,则调用函数 precompute_freqs_cis(d, seq_len) 后,生成结果为:
In [239]: freqs_cis
Out[239]:
tensor([[ 1.0000+0.0000j, 1.0000+0.0000j, 1.0000+0.0000j, 1.0000+0.0000j],
[ 0.5403+0.8415j, 0.9950+0.0998j, 0.9999+0.0100j, 1.0000+0.0010j],
[-0.4161+0.9093j, 0.9801+0.1987j, 0.9998+0.0200j, 1.0000+0.0020j]])以结果中的第二行为例(对应的 \(m = 1\)),也就是:
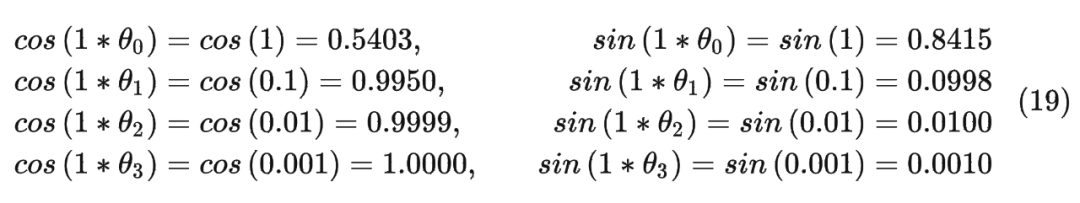
注意:在代码中是直接用freqs_cis[0] * xq_[0]的结果表示第一个 token 对应的旋转编码。其中将原始的 query 向量 转换为了复数形式。
这里为什么可以这样计算?
主要是利用了复数的乘法性质。
我们首先来复习一下复数乘法的性质:
因此要计算:
可以转化为计算:
小结
本文介绍了我们自研的旋转式位置编码RoPE以及对应的预训练模型RoFormer。从理论上来看,RoPE与Sinusoidal位置编码有些相通之处,但RoPE不依赖于泰勒展开,更具严谨性与可解释性;从预训练模型RoFormer的结果来看,RoPE具有良好的外推性,应用到Transformer中体现出较好的处理长文本的能力。此外,RoPE还是目前唯一一种可用于线性Attention的相对位置编码。
2D-ROPE
Transformer模型在视觉领域也大火,各种Vision Transformer(ViT)层出不穷,于是就有了问题:二维情形的RoPE应该是怎样的呢?乍一看上去,这个似乎应该只是一维情形的简单推广,但其中涉及到的推导和理解却远比我们想象中复杂,本文就对此做一个分析,从而深化我们对RoPE的理解。
二维RoPE
什么是二维位置?对应的二维RoPE又是怎样的?它的难度在哪里?在这一节中,我们先简单介绍二维位置,然后直接给出二维RoPE的结果和推导思路,在随后的几节中,我们再详细给出推导过程。
二维位置
在NLP中,语言的位置信息是一维的,换句话说,我们需要告诉模型这个词是句子的第几个词;但是在CV中,图像的位置信息是二维的,即我们需要告诉模型这个特征是在第几行、第几列。这里的二维指的是完整描述位置信息需要两个数字,并不是指位置向量的维数。
有读者可能想:简单展平后当作一维的处理不行吗?确实不大行,比如一个 \(h\times h\) 的feature map,位置 \((x,y)\) 展平后就变成了\(xh + y\),而位置 \((x+1,y)\) 和 \((x,y+1)\) 展平后就分别变成了\(xh+y+h\) 和 \(xh+y+1\),两者与 \(xh + y\) 的差分别是 \(h\) 和 \(1\)。然而,按照我们直观的认识,\((x+1,y)\)、\((x,y+1)\) 它们与 \((x,y)\) 的距离应该是一样的才对,但是展平后却得到了不一样的 \(h\) 和 \(1\),这未免就不合理了。
所以,我们需要专门为二维情形设计的位置编码,不能简单地展平为一维来做。
标准答案
经过后面的一番推导,得到二维RoPE的一个解为:
其中这个解很容易理解,它是两个一维RoPE组成的分块矩阵,实现上它就是将输入向量分为两半,一半施加 \(x\) 的一维RoPE,一半施加 \(y\) 的一维RoPE。由此形式我们也不难类比三维、四维等位置的RoPE。
矩阵(12)是一个正交矩阵,它满足两个关键性质:
1、相对性:即 \(\boldsymbol{\mathcal{R}}_{x_1,y_1}^{\top}\boldsymbol{\mathcal{R}}_{x_2,y_2}=\boldsymbol{\mathcal{R}}_{x_2-x_1,y_2-y_1}\),也正是由于这个性质,RoPE才具有通过绝对位置实现相对位置的能力;
2、可逆性:给定 \(\boldsymbol{\mathcal{R}}_{x,y}\) 可以反解出 \(x,y\),这意味着对位置信息的编码是无损的。
某种意义上来说,(12)是满足上述两个性质的最简单解,也就是说,虽然存在略有不同的解满足上述两个性质,但是它们形式上和实现上都相对复杂些。
推导思路
事后来看,RoPE其实就是找到了矩阵\(\boldsymbol{\mathcal{R}}_n=\begin{pmatrix}\cos n\theta & -\sin n\theta\\ \sin n\theta & \cos n\theta\end{pmatrix}\),使得满足“相对性”条件:
所以,不难想到,二维RoPE的基本要求也是满足相对性,即要找到矩阵\(\boldsymbol{\mathcal{R}}_{x,y}\) ,使得它满足二维的相对性条件\(\boldsymbol{\mathcal{R}}{x_1,y_1}^{\top}\boldsymbol{\mathcal{R}}{x_2,y_2}=\boldsymbol{\mathcal{R}}{x_2-x_1,y_2-y_1}\)。不过,如果仅仅是这个要求的话,可行解就很多了,比如直接让
但这个解的问题是,我们无法从 \(x+y\) 逆向推出 \((x,y)\),这意味着这个选择对位置信息来说是有损的,所以我们需要多一个“可逆性”,保证可以从位置矩阵中无损地重构出原始位置信号。
对此,我们有两个比较自然的途径选择:
- 四元数;
- 矩阵指数
接下来我们将会逐一介绍它们。
四元数
在一维RoPE的推导中,我们主要以复数为工具,而四元数(Quaternion)是复数的推广,它同时也保留了复数的很多性质,所以用它来推导二维RoPE也算是一个自然的思路。不过很遗憾,这是一条走不通的途径,思路可以参考Transformer升级之路:4、二维位置的旋转式位置编码
矩阵指数
四元数推导走不通,那么或许使用一般的矩阵分析可以走得通。事实上确实如此,在这一节中,我们将利用矩阵指数给出一个推导结果。
矩阵指数
这里的矩阵指数,并不是神经网络的用指数函数作为激活函数的逐位运算,而是是按照幂级数定义的运算:
其中 \(\boldsymbol{B}^k\) 是指按照矩阵乘法将 \(k\) 个 \(\boldsymbol{B}\) 连乘。
矩阵指数是非常重要的一种矩阵运算,它可以直接写出常系数微分方程组 \(\frac{d}{dt}\boldsymbol{x}_t=\boldsymbol{A}\boldsymbol{x}_t\) 的解:
当然这跟本文的主题关系不大。对于RoPE的推导,我们主要利用到矩阵指数的如下性质:
也就是说,如果 \(\boldsymbol{A},\boldsymbol{B}\) 的乘法可以交换,那么矩阵指数就可以像数的指数一样将乘法转换为加法。不过要注意这是一个充分不必要条件。
至于怎么把矩阵指数算出来,这里没法再展开介绍了,但是很多软件库已经自带了矩阵指数运算,比如数值计算库scipy和tensorflow都有expm函数,而符号计算的话,Mathematica里边有MatrixExp函数。
一维通解
为什么能够将RoPE跟矩阵指数联系起来呢?因为一维的RoPE存在比较简单的指数表达式:
于是笔者开始思考如下形式的矩阵作为RoPE的解:
其中 \(\boldsymbol{B}\) 是一个跟 \(n\) 无关的矩阵。RoPE的必要条件是满足“相对性”(13),于是我们分析
这里先假设 \(\boldsymbol{B}^{\top},\boldsymbol{B}\) 是可交换的,那么根据(15)有
要让 \(m\boldsymbol{B}^{\top} + n\boldsymbol{B}=(n-m)\boldsymbol{B}\),只需要满足
这便是“相对性”给出的约束条件,刚才我们还假设了 \(\boldsymbol{B}^{\top},\boldsymbol{B}\) 是可交换的,现在可以检验满足这个等式的 \(\boldsymbol{B}^{\top},\boldsymbol{B}\) 一定是可交换的,所以结果是自洽的。
这也就是说,对于任何满足 \(\boldsymbol{B}^{\top} + \boldsymbol{B} = 0\) 的矩阵 \(\boldsymbol{B}\),\(\exp n\boldsymbol{B}\) 都是 方程21 的解,并且还可以证明它一定是正交矩阵。当然,根据 \(\exp n\boldsymbol{B}=\left(\exp \boldsymbol{B}\right)^n\),我们更直接的得到:对于任意正交矩阵\(\boldsymbol{O},\boldsymbol{\mathcal{R}}_n=\boldsymbol{O}^n\) 都是方程21 的解。
对于 \(2\times 2\) 的矩阵来说,\(\boldsymbol{B}^{\top} + \boldsymbol{B} = 0\) 的通解是 \(\boldsymbol{B}=\begin{pmatrix}0 & -\theta\\ \theta & 0\end{pmatrix}\),于是就有了如(16)的解。
二维约束
类似地,对于二维RoPE,我们考虑
作为候选解。重复上述关于“相对性”条件的推导:先假设 \(x_1\boldsymbol{B}_1^{\top} + y_1\boldsymbol{B}_2^{\top}与x_2\boldsymbol{B}_1 + y_2\boldsymbol{B}_2\) 是可交换的,那么我们可以得到如下约束条件:
然而,\(x_1\boldsymbol{B}_1^{\top} + y_1\boldsymbol{B}_2^{\top}\)与 \(x_2\boldsymbol{B}_1 + y_2\boldsymbol{B}_2\) 可交换,意味着\((\boldsymbol{B}_1,\boldsymbol{B}_1^{\top})、(\boldsymbol{B}_2,\boldsymbol{B}_2^{\top})\)、\((\boldsymbol{B}_1,\boldsymbol{B}_2^{\top})和(\boldsymbol{B}_2,\boldsymbol{B}_1^{\top})\) 都可交换,但是上述两个约束只能保证\((\boldsymbol{B}_1,\boldsymbol{B}_1^{\top})\) 和 \((\boldsymbol{B}_2,\boldsymbol{B}_2^{\top})\)可交换,不能保证后两者的交换性,所以我们需要把它作为约束条件补充上去,得到:
不难证明在前两个条件下,新增的约束条件也相当于\(\boldsymbol{B}_1 \boldsymbol{B}_2 = \boldsymbol{B}_2 \boldsymbol{B}_1\)。
RoPE现身
由于满足前两个条件的 \(2\times 2\) 矩阵只有一个独立参数,不满足“可逆性”,所以我们至少要考虑 \(3\times 3\) 矩阵,它有3个独立参数
为了保证可逆性,我们不妨设 \(\boldsymbol{B}_1,\boldsymbol{B}_2\) 是“正交”的,比如设:
不失一般性还可以设 \(a=1\),那么由条件(33) 解得 \(b=0,c=0\),即 \(\boldsymbol{B}_2\) 只能是全零解,这不符合我们的要求。Mathematica的求解代码为:
B[a_, b_, c_] = {{0, -a, -b}, {a, 0, -c}, {b, c, 0}};
B1 = B[1, 0, 0];
B2 = B[0, b, c];
Solve[{Dot[B1, B2] == Dot[B2, B1]}, {b, c}]
因此,我们至少要考虑 \(4\times 4\) 矩阵,它有6个独立参数,不失一般性,考虑正交分解:
解得
求解代码:
B[a_, b_, c_, d_, e_,
f_] = {{0, -a, -b, -d}, {a, 0, -c, -e}, {b, c, 0, -f}, {d, e, f,
0}};
B1 = B[1, b, c, 0, 0, 0];
B2 = B[0, 0, 0, d, e, f];
Solve[{Dot[B1, B2] == Dot[B2, B1]}, {b, c, d, e, f}]
可以发现结果没有对 \(f\) 提出约束,所以从最简单起见,我们可以让 \(f=1\),剩下的 \(b,c,d,e\) 全部为0,此时
可以增加个参数 \(\theta\),完成展开,就得到:
小结
本节介绍了我们对RoPE的二维推广,主要以“相对性”、“可逆性”为出发点来确定二维RoPE的最终形式,尝试了四元数和矩阵指数两种推导过程,最终通过矩阵指数来给出了最终的解,从推导过程中我们还可以深化对RoPE的理解。
多模态位置编码
回忆旋转位置
RoPE名称中的“旋转”一词,来源于旋转矩阵 \(\boldsymbol{\mathcal{R}}_n=\begin{pmatrix}\cos n\theta & -\sin n\theta\\ \sin n\theta & \cos n\theta\end{pmatrix}\),它满足
这样一来对于 \(\boldsymbol{q},\boldsymbol{k}\)(假设为列向量)的内积就有
最左边的式子中,\(\boldsymbol{\mathcal{R}}_m\boldsymbol{q},\boldsymbol{\mathcal{R}}_n\boldsymbol{k}\) 是独立进行的,不涉及到 \(m,n\) 的交互,所以它形式上是绝对位置,但最右端的等价形式只依赖于相对位置 \(n-m\),所以跟 Dot-Product 的Attention结合之后,它实质表现为相对位置。这个特性也让RoPE具备平移不变性:因为\((n+c) - (m+c) = n-m\),所以在应用RoPE之前全体绝对位置都加上一个常数,那么Attention的结果理论上不会变化(实际上受限于计算精度,可能有微小误差)。
以上是 \(\boldsymbol{q},\boldsymbol{k}\in\mathbb{R}^2\) 的形式,对于 \(\boldsymbol{q},\boldsymbol{k}\in \mathbb{R}^d\)(其中 \(d\) 是偶数),我们需要一个 \(d\times d\) 的旋转矩阵,为此我们引入\(d/2\) 个不同的 \(\theta\),构造分块对角矩阵
从实现上看,就是将 \(\boldsymbol{q},\boldsymbol{k}\) 两两分组,每组取不同的 \(\theta\) 进行二维的旋转变换,这些是已有的RoPE内容,就不再详细展开了。原则上来说,我们只需要找到一个最低维的解,就可以通过分块对角的方式推广到一般维度,因此下面的分析都只考虑最小维度。
而对于二维旋转位置编码,当我们谈到“维度”这个概念时,可能会有多种含义,比如刚才我们说\(\boldsymbol{q},\boldsymbol{k}\in \mathbb{R}^d\),这就是说 \(\boldsymbol{q},\boldsymbol{k}\) 都是\(d\)维向量,但本文所聚焦的RoPE-1D、RoPE-2D,它并不是指这个维度,而是指记录一个位置所需要的维度。

比如,我们要文本的某个token的位置,那么只需要一个标量 \(n\),记录它是第\( n\) 个token。但对于图像来说,即便进行了patchify,它通常也会保留width和height两个方向维度,所以我们需要一对坐标\((x,y) \)才能准确编码某个patch的位置:

上面介绍的 \(\boldsymbol{\mathcal{R}}_n\),它只编码了一个标量\(n\),所以它是RoPE-1D,而为了更合理地处理图像输入,我们要推广到相应的RoPE-2D:
很明显,这只是\(\boldsymbol{\mathcal{R}}_x\) 和 \(\boldsymbol{\mathcal{R}}_y\) 以分块对角的形式组合在一起,因此也很自然能将它推广到3D甚至更高维度。从实现上来理解就是更简单了,它就是将 \(\boldsymbol{q},\boldsymbol{k}\) 都切分为两半(3D就是三等分、4D就是四等分,依此类推),每一半都是 \(\mathbb{R}^{d/2}\) 的向量,然后一半做 \(x\) 的RoPE-1D,另一半做 \(y\) 的RoPE-1D,最后再拼起来。
需要指出的是,从对称性和简洁性考虑,上面构造的 \(\boldsymbol{\mathcal{R}}_{x,y}\) 中对 \(x,y\) 我们使用了相同的 \(\theta\),但这原则上是非必须的,在适当情况下我们分别给 \(x,y\) 配置略有不同的\(\theta\)。
强行降维
现在我们看到,文本的位置是一个标量 \(n\),图片的位置则是一个向量\((x,y)\),两者并不一致,因此在处理图文混合输入时就需要一些技巧,来调和两者之间的不一致性。
最直接的方案,文章开头已经说了,就是直接展平图片为一维向量序列,然后就当作普通文本来处理,文本怎么加位置编码它就怎么加位置编码。这种思路自然是非常通用的,不限于加RoPE,也可以加任何绝对位置编码,笔者目测已有的一些多模态模型,如Fuyu-8b、Deepseek-VL、Emu2等,都是这样做的,可能细节处理上会有所不同,比如遇到不同行的patch可以考虑加个表示[SEP]的special token来分隔:

这个方案也契合了当前主流的Decoder-Only架构,因为Decoder-Only意味着即便不加位置编码,它也不是置换不变的,因此必须人为指定我们认为最佳的输入顺序,而既然要指定输入顺序了,按照所指定的顺序使用一维的位置编码也是很自然的选择。此外,在纯文本时这种方案的模型跟普通纯文本LLM无异,所以这也允许我们将训练好的文本LLM来继续训练成一个多模态模型。
然而,从笔者的角度看,位置编码的概念本身不应该和Attention的用法绑定,它应该普适于Decoder、Encoder乃至任意的Attention Mask。另一方面,保持位置的二维性才能最大程度上保留我们关于相近位置的先验,比如我们认为位置\((x+1,y)\) 和 \((x,y+1)\) 都应该跟 \((x,y)\) 具有相近的距离,但如果(先水平后垂直)展平的话,\((x,y)\) 变为 \(xw + y\),而 \((x+1,y)\) 和 \((x,y+1)\) 分别变为了 \(xw+y+w\) 和 \(xw+y+1\),前者与\(xw + y\) 的距离就依赖于 \(w\) 而后者是固定的 \(1\)。当然,我们还可以指定其他制定顺序,但不管怎么指定顺序,都无法完全兼容所有邻近位置的相近性,毕竟少了一个维度,可表达的相似性就少了很多。
统一升维
从向量空间的角度看,一维的标量可以看成一个特殊的二维向量,因此相比于展平为一维,如果我们反过来将所有输入的位置都统一到二维,原则上有更大的操作空间。
为此,我们可以考虑一种常见的排版方式:以图片为分隔符,对文本进行分段,连续的文本都视为一行,图片则视为多行文本,那么整个图文混合输入就相当于一篇多行长文,每个文本token或者图片patch,都有自己所属的行数 \(x\) 以及行内的顺序 \(y\),这就给所有的输入单元(token或者patch)都赋予了一个二维位置\((x,y)\),于是可以统一用RoPE-2D(其他2D形式的位置编码理论上也可以)来编码位置,同时还保持了原本图片位置的二维性。
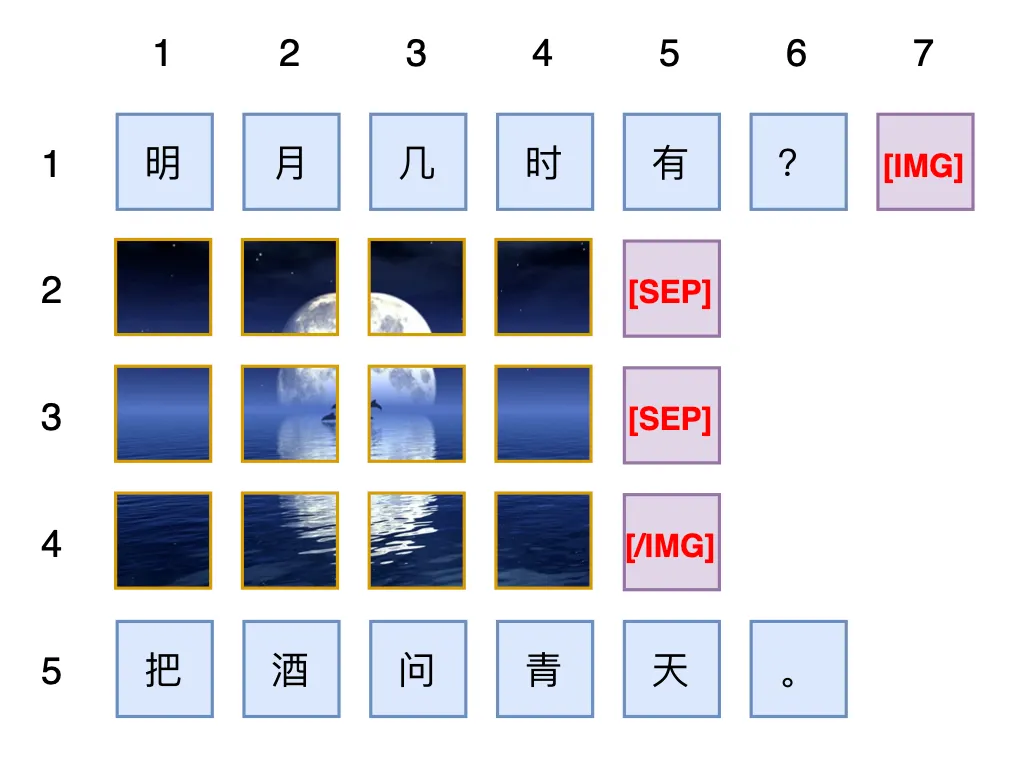
很明显,该方案的主要优点是非常直观,它直接跟实际的视觉排版相对应,便于理解和推广。但它也有一个非常明显的缺点,那就是对于纯文本输入,它无法退化为RoPE-1D,而是变成了 \(x\) 始终为1的RoPE-2D,这样从已训练好的文本LLM出发来训练多模态LLM的可行性就值得怀疑。此外,以图片作为分割点的话,当图片比较多时,可能会让文本被分割得过于“支离破碎”,具体表现包括每一段文本的长度波动太大、本该连续的文本被强行换行等,这些都可能成为限制效果的瓶颈。
合二为一(Rope-Tie)
如果要无损保留图片patch的位置信息,那么统一到二维然后用RoPE-2D(或者其他2D形式的位置编码)看上去是必然的选择,所以上一节的方案已经是走在了正确的方向上,我们需要进一步思考的是如何能够让它对于纯文本输入能够退化为RoPE-1D,以兼容已有的文本LLM。
首先,我们在前面已经提到过,\(\boldsymbol{\mathcal{R}}_{x,y}\) 是 \(\boldsymbol{\mathcal{R}}_x\) 和 \(\boldsymbol{\mathcal{R}}y\) 的分块对角组合,所以 \(\boldsymbol{\mathcal{R}}_{n,n}\) 是两个 \(\boldsymbol{\mathcal{R}}_n\) 的分块对角组合,而RoPE-1D的 \(\boldsymbol{\mathcal{R}}_n^{(d\times d)}\) 也是多个不同 \(\theta\) 的 \(\boldsymbol{\mathcal{R}}_n\) 的分块对角组合,由此可见,只要我们从\(\boldsymbol{\mathcal{R}}_n^{(d\times d)}\) 选取不同的 \(\theta\) 给 \(x,y\),那么 \(\boldsymbol{\mathcal{R}}_{n,n}\) 就可以看成是RoPE-1D(即\(\boldsymbol{\mathcal{R}}_n^{(d\times d)}\))的一部分。这样看来,要想RoPE-2D能退化为RoPE-1D,那么文本的位置应该采取 \((n,n)\) 的形式,而不是像上一节那样用其他方式指定一个行号。
然后,在图片内部,我们则使用常规的RoPE-2D,对于单张 \(w\times h\) 个patch的图片来说,它的二维位置坐标展平后是
如果这张图片位于一个长度为 \(L\) 的句子后面,我们这个句子的最后一个token的位置编码就是 \((L,L)\),于是这张接在句子后面的图片的位置编码看上去应该是
但这并不完美,因为句子的最后一个token的位置是\((L,L)\),图片第一个patch的位置是\((L+1,L+1)\),它们相差 \((1,1)\);假设这张图片后面再接一个句子,那么设该句子的第一个token的位置是 \((K,K)\),图片的最后一个patch的位置则是 \((L+h,L+w)\),当 \(w\neq h\) 时,不管我们怎么设置 \(K\),都不可能让\((K,K)\) 与 \((L+h,L+w)\) 的差为 \((1,1)\),即图片关于左右的句子存在不对称性,这就显得不够优雅。
为了改进这一点,我们可以将图片的 \(x,y\) 分别乘以正数 \(s,t\):
只要 \(s,t\neq 0\),那么这个缩放对位置信息是无损的,因此这样的操作是允许的。而引入scale之后,假设句子的最后一个token的位置依旧是 \((L,L)\),那么图片的位置同样是上述序列都加上\(L\),此时“句子的最后一个token的位置”与“图片第一个patch的位置”之差就是\((s,t)\),如果我们希望“图片后面的句子的第一个token的位置”与“图片最后一个patch的位置”之差也是\((s,t)\),那么就应该有
考虑到 \(h,w\) 的任意性,并且希望保证位置ID都是整数的话,那么最简单的一个解自然是\(s=w+1,t=h+1\),新句子第一个token的位置将会是 \(K=L+(w+1)(h+1)\)。一个具体的例子如下图所示:

延伸思考
左边句子最后一个token的位置是 \(L\),右边句子第一个token的位置是 \(K=L+(w+1)(h+1)\),如果中间部分也是一个句子的话,那么可以推出该句子有 \((w+1)(h+1)-1\) 个token,这也等价于说如果两个句子之间夹着一个 \(w\times h\) 的图片,那么对这两个句子的相对位置来说等价于隔着一个\((w+1)(h+1)-1\) 个token的句子。这个数字看起来有点不自然,因为看上去 \(wh\) 才是完美答案,但可惜这是保证所有位置ID都是整数的最简单解。如果允许非整数的位置ID,那么可以约定\(w\times h\) 的图片等价于 \(wh\) 个token,反过来推出
可能有读者要问:如果是两张不同大小的图片相邻,是不是就没有这样对称的方案了?这其实也不难,只要每张图片的前后,我们都加入special token来标记,如[IMG]、[/IMG],并且special token当作普通文本token来编码位置,这样就直接避免了两张图片直接相邻的情况(因为按照约定,同一张图片的patch之间必然夹在[IMG]和[/IMG],这两个token当作文本来处理,所以就等价于说每一张图片必然夹在两个文本之间)。此外,上述介绍中没有提及[SEP],如果有需要自行引入即可,事实上只有用patch by patch的自回归方式做图片生成时,才有必要引入[SEP],如果图片单纯是作为输入,或者图片生成用扩散模型来做,那么[SEP]则是多余的。
至此,我们关于将RoPE推广到图文混合输入的推导已经完成,如果需要一个名字,可以将最后的方案称之为“RoPE-Tie(RoPE for Text-image)”。不得不说的是,最后的RoPE-Tie并不算太漂亮,以至于给人一种“雕花”的感觉。从效果上来看,相比直接展平为一维用RoPE-1D,换用RoPE-Tie之后也不见得会有什么提升,它更多是笔者的强迫症的一个产物。所以,对于已经scale到了一定规模的多模态模型,就没有必要做出什么改动了,但如果还没有起步或者刚刚起步,那么不妨尝试一下RoPE-Tie。
等价对称 (RoPE-Tie-v2)
我们确定了图文混合模态统一用RoPE-2D的方案,并且由向后兼容性确定了位置 \(n\) 的文本Token的二维位置应该取 \((n,n)\),从而完成了文本部分的位置编码设计。接下来,我们需要构思的是图像部分的位置编码。
如果输入只有一张 \(w\times h\) 个Patch的图像,那么它的位置坐标自然就是各个Patch本身的坐标,即
我们这展示的是绝对位置,但实际的效果是相对位置,相对位置的特点是跟位置偏置无关,所以我们可以给每个坐标都加上 \((\beta_1,\beta_2)\) 而不改变效果;其次,我们可以给每个坐标都乘以 \((\gamma_1,\gamma_2)\) ,这样允许我们按需调整相邻位置的间隔。将这两点结合起来,我们可以得到图像的一般化二维位置为
现在我们考虑左右两段文本夹着中间一张图像时,\(\beta_1,\beta_2,\gamma_1,\gamma_2\) 该怎么选取。
首先,我们假设文本的Token和Patch具有一定的等价性:经过合理的Patchify后每个Patch的地位跟Token等价(An Image is Worth xxx Tokens),这意味着对于两段文本来说,它们相当于夹着一个wh个Token的句子,所以如果左段文本最后一个Token的位置是 \((L,L)\),那么右段文本第一个Token的位置就是\((L+wh+1, L + wh + 1)\)。
接着,我们还需要引入对称性——具体来说,图像的第一个Patch的位置是\((\beta_1 + \gamma_1,\beta_2 + \gamma_2)\),最后一个Patch的位置是\((\beta_1 + h\gamma_1,\beta_2 + w\gamma_2)\),我们认为【图像第一个Patch】与【左段文本最后一个Token】的位置差,等于【右段文本第一个Token】与【图像最后一个Patch】的位置差,即
这里边有四个未知数 \(\beta_1,\beta_2,\gamma_1,\gamma_2\),但只有两个等式,所以有无穷多组解。我们可以简单地取\(\gamma_1=\gamma_2=1\),继而解得
这个方案我们暂时可以称之为RoPE-Tie-v2或者RoPE-TV吧。
优劣分析
根据这个结果,当句子后面接一张 \(w\times h\) 的图像时,只需要按照上述计算计算出\((\beta_1,\beta_2)\),然后加到常规的二维RoPE (17)中去,就得到了图像部分的位置坐标了,如下图所示

作为对比,RoPE-Tie,其位置坐标如下图所示:

事实上,RoPE-Tie的出发点同样包括兼容性和对称性,但没有严格遵循等价性,并且RoPE-Tie默认了\(\beta_1=\beta_2=L\),以及没有限定 \(w\times h\) 个Patch等价于 \(wh\) 个Token,最终推出了一组整数解(如果不要求整数解也可以满足等价性):
从如今的视角来看,RoPE-Tie的默认设置其实并不是很理想,所以本文重新选择了\(\gamma_1=\gamma_2=1\),并确保等价性,然后反推出\(\beta_1,\beta_2\)。
那新方案有什么好处呢?首先,RoPE-Tie中图像内的相对位置跟它的大小有关,而新方案中Patch的间隔是固定的(0,1)和(1,0),这可以让Patch的尺度更为一致。举个例子,一张\(128*128\)的图像以及该图的上半部份(即\(128*64\)的子图),由于两者高度不一样,所以RoPE-Tie后它们横向的位置间隔并不一样,这意味着同样位置、同样含义的两个Patch在加了RoPE-Tie后的距离(尺度)变得不一致了,这看起来并不合理,而新方案没有这个问题。
其次,RoPE-Tie中图像与左右文本的间隔,跟图像内部Patch的间隔一样都是(\(\gamma_1,\gamma_2\)),而新方案中文本到图像、图像到文本之间会出现一个比较大的间隔 \(\frac{1}{2}(wh - h, wh-w)\),然后文本内部、图像内部则都是固定的均匀间隔。直觉上,这种不同模态之间比较大的位置跳跃,可以更好地实现“模态隔离”,让单个模型既能更好地处理单模态内容,又保留了多模态之间的交互,这跟我们通常在左右加[IMG]和[/IMG]两个Special Token来标记出图像具有异曲同工之处。
三维困境
在RoPE-Tie中,并没有讨论到“文本-视频”混合模态的位置编码,这一节我们来补充讨论完整。
直观来看,对于视频输入我们可以有两种处理方式。第一种方式就是简单地将视频当成多张图片处理(必要时加个[VIDEO]、[/VIDEO]的标记),这样我们就不需要针对视频提出新的位置编码了,沿用“文本-图像”的混合位置编码结果就行,但这样丧失了同一视频不同帧之间的对齐关系,可能不是太完美,例如“第1帧的第1个Patch”跟“第2帧的第1个Patch”和“第1帧的第2个Patch”,应该有差不多的邻近关系,但展平当多张图片处理就体现不出这一点。
第二种方式则是将“文本-图像”的结果平行地推广到“文本-视频”中。对于一个\(w\times h\times t\) 的视频(画面为\(w\times h\),一共\(t\) 帧),它的位置坐标是三维的\((x,y,z)\),根据相同的兼容性、等价性和对称性,我们可以将(19)推广成
如果还是设\(\gamma_1=\gamma_2=\gamma_3=1\),我们得到
这样做完整了保留了视频位置的三维性,看起来会更优雅一些,但笔者认为它仍有一些美中不足之处。
这个美中不足源于笔者对视频的时间维度的不同理解:视频的三维,实际上是“2个空间维度+1个时间维度”,跟真实世界的三维立体的“3个空间维度”不一样。按照笔者的观点,视频的时间维度跟两个空间维度是不平权的,时间维度更像是文本从左往右的书写方向,所以笔者想象中的完美多模态LLM,应该能像文本LLM续写文本一样,理论上能够以自回归的方式无限地续作视频,直到出现[EOS]标记。
刚才我们提了两种“文本-视频”混合编码方案,第一种直接当作多张图片处理,这种方案是可以无限自回归生成视频的,但第二种看上去更完美的方案反而不行,因为它的 \(\beta_1,\beta_2,\beta_3\) 是依赖于 \(t\) 的,这意味着我们需要提前知道生成多少帧的视频,换句话说,第二种方案并不是不能用自回归的方式生成视频,而是需要提前确定帧数,这在笔者看来是不符合时间维度的理想特性的(时间,应该可以无约束地往前推进)。
可能有读者疑问:为什么图像就不介意 \(\beta_1,\beta_2\) 中依赖于 \(w,h\) 呢?也就是说为什么图像生成不介意事先知道图像大小呢?这是因为图像有两个方向,就算我们用自回归的方式生成图像,也必须至少知道一个方向的大小,才能告诉模型及时“换行”,以生成一张完整的二维图像。而图像的两个空间维度是平权的,单知其一倒不如全部知道,所以我们能够接受事先确定图像大小。
相关工作
前段时间,阿里开源了名为“Qwen2-VL”的多模态模型,介绍中提到自己提出了一种多模态旋转位置编码(M-ROPE),引起了笔者的兴趣。经过阅读源码(链接),发现M-RoPE实际上就是沿用了RoPE-Tie的兼容性思想,但没有保留对称性和等价性。

用本文的记号,M-RoPE实际上就是取了\(\beta_1=\beta_2=\beta_3=L,\gamma_1=\gamma_2=\gamma_3\)(对于“文本-视频”混合模态),然后视频右段的文本的第一个Token的位置,直接取视频最大的位置坐标加1。这样如果还是用自回归的方式生成视频,确实也不用提前确定帧数,但牺牲了对称性和等价性。
对称性和等价性有多重要呢?笔者不清楚答案,这需要充分实验来验证。但如果仅仅是头脑风暴的话,笔者猜测可能会影响极端情形的表现,比如对于M-RoPE来说,如果是画面很小但时间很长的视频,它的空间维度的位置坐标相对于左段文本来说是连续的,但相对于右段文本来说则是突变了,直觉上会使得文本和视觉的交互更不友好。
再比如一个\(w=h=t=n\) 的视频,直觉上它等效于\(n^3\)个Token,但如果按照M-RoPE的规则,如果两段文本夹着这样一个视频,只是等价于夹着一个 \(n\) 个Token的文本,换言之在大小为 \(n\) 的相对距离内放下了\(n^3\)个Token,会不会导致信息密度过大而增加模型理解难度了?
当然,对于NoPE都可能Work的Decoder-only LLM来说,这些问题也可能是笔者多虑了。
小结
本文分享多模态位置编码的后续思考,提出了构建多模态位置编码的三个原则:兼容性、等价性和对称性,改进了之前提出过的RoPE-Tie,最后讨论了“文本-视频”混合模态的位置编码设计和困难,以及Qwen2-VL的M-RoPE与RoPE-Tie的联系等。
Reference
Transformer升级之路:2、博采众长的旋转式位置编码
Transformer升级之路:4、二维位置的旋转式位置编码