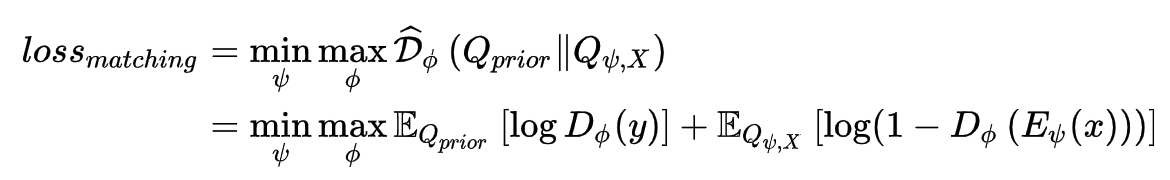Deep InfoMax(DIM)

Dec 29, 2024
2 views
Self-Supervised
# Self-Supervised # 对比学习

相关内容

  • 自监督学习（Self-supervised）：属于无监督学习，其核心是自动为数据打标签（伪标签或其他角度的可信标签，包括图像的旋转、分块等等），通过让网络按照既定的规则，对数据打出正确的标签来更好地进行特征表示，从而应用于各种下游任务。
  • 互信息（Mutual Information）：表示两个变量 \(X\) 和 \(Y\)之间的关系，定义为：
  • 噪声对抗估计（Noise Contrastive Estimation, NCE）：在NLP任务中一种降低计算复杂度的方法，将语言模型估计问题简化为一个二分类问题。

Introduction

无监督学习一个重要的问题就是学习有用的 representation，本文的目的就是训练一个 representation learning 函数（即编码器encoder） ，其通过最大编码器输入和输出之间的互信息(MI)来学习对下游任务有用的 representation，而互信息可以通过 MINE 的方法进行估算。

作者还提到，直接最大化全部输入和编码器的输出（即全局的MI）更适合于重建性的任务，而在分类的下游任务上效果不太好。而最大化输入的局部区域（例如不是完整的图片，而是图片中的一块）和输出（即学到的representation）的平均互信息在下游任务（如图像分类）上的效果更好。

因为这种方法类似于对抗自动编码器(AEE, adversarial autoencoders)的，将MI最大化和先验匹配结合起来，根据期望的统计特性约束 representation，并且还与 infomax 的优化规则密切相关，因此作者称其为 Deep InfoMax(DIM).

因此，文章的主要贡献如下：

  • 提出了 Deep InfoMax(DIM)，可以同时估算和最大化输入数据和高级representation之间的互信息(MI)
  • 作者提出的最大化互信息的方法，可以根据下游任务是分类还是重建，来对优化全局还是局部的信息进行调整。
  • 使用对抗学习约束representation，来使其具有特定于先验的期望统计特征
  • 介绍了两种测量 representation 质量的新方法，一个基于Mutual Information Neural Estimation(MINE)，一个基于neural dependency measure(NDM)  ，并用它们将DIM与其他无监督学习方法进行比较

算法模型

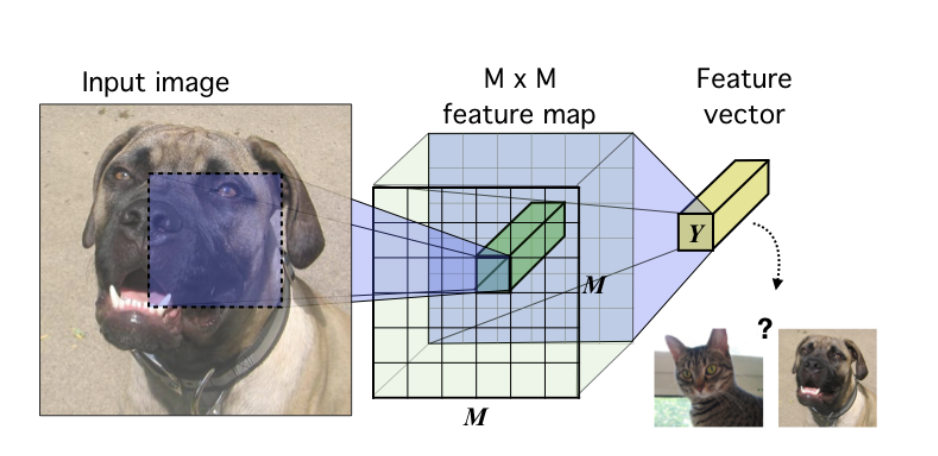
image

上图是一个图像数据的基本编码器模型，编码器设为\(E\)，输入一张图片\(X\)，经过几层卷积，得到一个\(M*M*C\) 的特征图，再将这些特征经过卷积展开或全连接层的计算，得到一个一维的特征向量Y，就是输入数据的高层语义信息。

论文指出，基于DIM的编码器目标是：

  1. 互信息最大化。找到一组编码器的参数 \(\phi\)，使得 \(I(X;E_\phi(X))\) 最大，即输入数据和其高层语义特征的互信息最大，根据下游任务，可以将式子中的 \(X\) 替换为输入数据的局部特征；
  2. 结构约束。特征的边缘分布应该和先验分布一致，这里是指通过对抗机制构成的约束。
    因此，在上面基础编码器的基础上，论文设计了如下图的DIM框架：

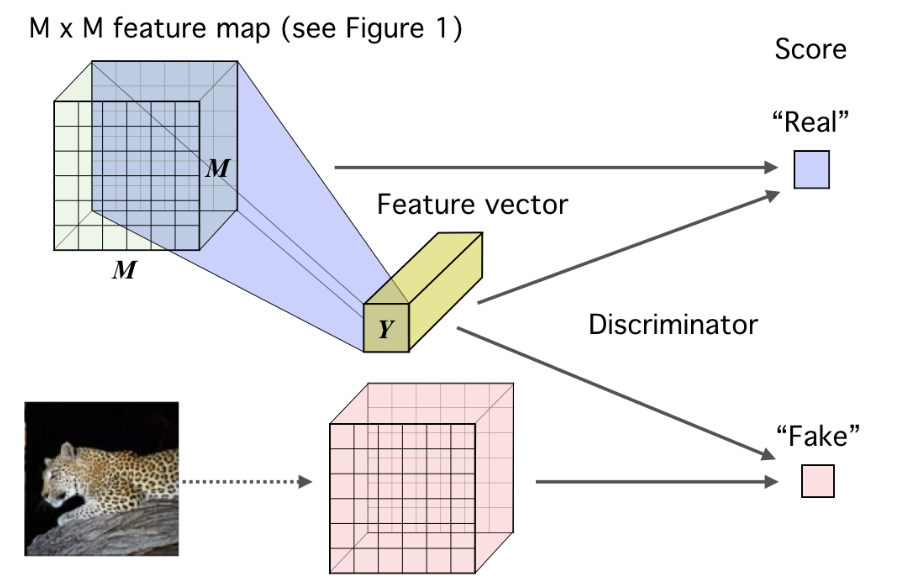
image

主要思想是，一张图的全局特征 Y 和它的局部特征应该高度相关，和另一张图的局部特征应该不相关。图中蓝色特征图来自于当前目标图片，继而解析出它的高层特征Y，而红色特征图则来自另一张图片，Y和蓝色特征的互信息应该较大，和红色特征的互信息应该较小，于是设置一个判别器，用于估计全局特征和局部特征的互信息，为不同的信息组合方式打分。
“原配”的全局和局部特征组合，可以视作语义信息的联合分布，而非“原配”的错误的组合，可视为边缘分布。判别器的目标是尽量区分这两种分布，编码器的目标则是欺骗判别器，也就是对每个不同的输入图片，都编码出一个特定的、高度相关的语义信息。

论文中还提到，当直接把一张完整的图片送入编码器得到特征图时，可能对于分类任务是不利的，因为图片中可能包含大量无信息的噪声，这会引起特征图的不准确，因此当下游任务是分类任务时，可以将图片局部块（patches）输入进编码器。具体操作看下图：

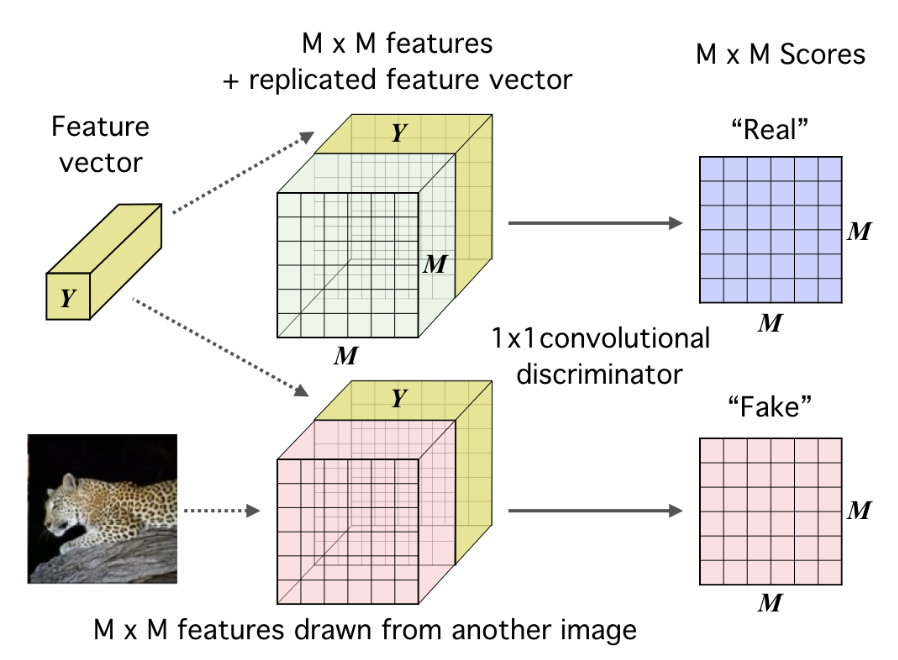
image

也就是将全局特征Y分别匹配到局部特征图的每个特征点上，图中复制了\(M \times M\) 次 \(Y\) 特征，再和特征图拼接，然后对于每个特征点，再接上一个\(1\times 1 \times N\) 的判别器卷积结构，对每个特征点进行互信息的打分，因此输出的是一张\(M\times M\) 的分数特征图，最后计算 loss时取每个点的平均值。对负样本也是同样的操作，主要思想还是和同一张图的特征相关度最大，和其他图的相关度最小。
论文中认为这样的操作，可以促使编码器解析出图中各部分都共享的特征，也就是更加具有代表性的信息。

以上的操作都是为了增大特征表示和输入数据（或是第层特征）之间的互信息，之前有提到，为了实现统计特征约束，DIM采用了对抗匹配先验分布的方式来控制表示特征。

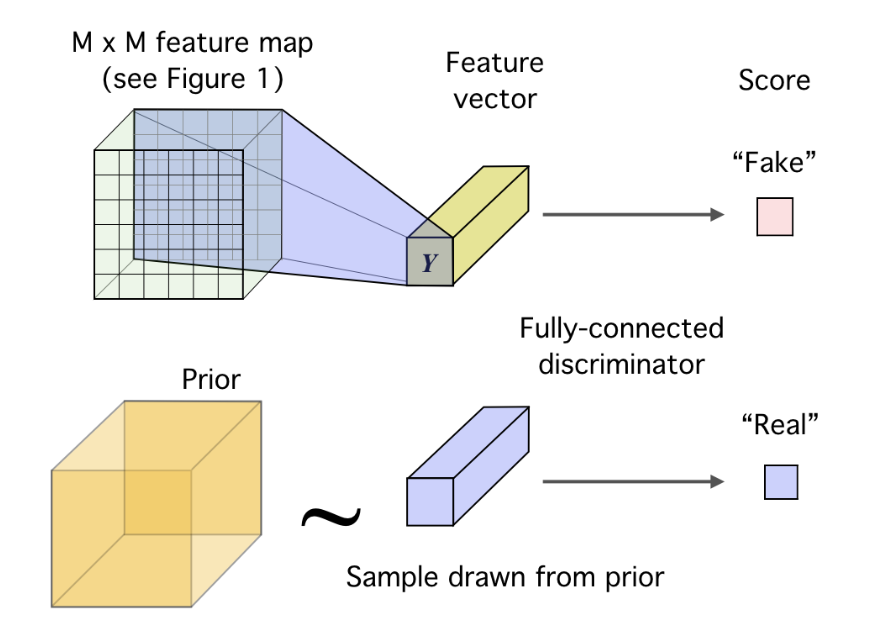
image

因为好的表示学习应该是独立、可控的，所以编码器输出的特征分布和先验分布应该相近，图中判别器的目标是区分特征分布的真伪，而编码器则是尽量欺骗判别器，解析出更贴近真实分布的特征。

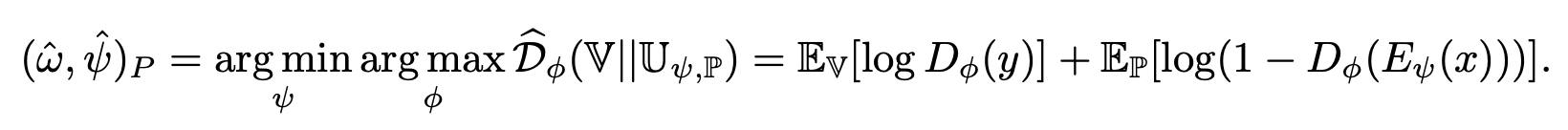
image

损失函数的形式就是对抗损失，和GAN相比编码器就相当于生成器，\(x\) 经过编码器得到的是特征分布，\(y\) 则是数据特征的先验分布。

优化目标

既然要训练 Discriminator ，就不得不提一下 DIM 的损失函数，那么就得先说一下其优化目标。

首先，我们定义一些数学符号：

  • \(x\in X\) 为 image 数据集；编码器 encoder 为  \(E_\psi=h_\psi\odot f_\psi\)（  \(\odot\) 表示是由后面那两个函数组成 ）； \(f_\psi(x)\)表示将原始图像 \(x\) 映射到 feature map；\(h_\psi(f_\psi(x))\)  表示将 feature map 再映射到最后的输出 representation，即 \(y=h_\psi(f_\psi(x))=E_\psi(x)\in Y\) 。

  • 将样本从 \(f_\psi(X)\) 经过 \(h_\psi\) 得到的 \(y\in Y\) 的分布，也叫做 ”push-forward distribution“（目前还不是很理解这个名词），记作 \(Q_{\psi,X}\)
    而 DIM 最终的优化目标也就是以下两点：

  • 最大化 \(f_\psi(X)\) 和 \(Y\) 之间的互信息。（作者根据具体任务的不同，又分为了 global 和 local 两种，后面再提）

  • 在最终的 representation 中再加入一个统计性的约束，使得到的 \(y\) 的分布（push-forward distribution）\(Q_{\psi,X}\)  尽量与先验分布 \(Q_{prior}\) 相匹配，有点类似对抗自编码器（AAE）。

Loss Function

Global Infomax

知道了优化目标，下面就是如何去建立和推导该目标的数学表达方式。

我们首先解决第一个优化目标，也就是最大化互信息。互信息就是衡量两个变量的相关性，如果\(X\)和 \(Y\) 相互独立，即 \(P_{XY}=P_XP_Y\)，那么它们的互信息 \(I(X;Y)\) 也就为0。互信息的定义如下：

\[ \mathcal{I}(X;Y)=\sum_{X,Y}logP(X,Y)\frac{P(X|Y)}{P(X)} \]

KL散度则是衡量同一个随机变量两个分布之间的差异，其值越小，说明分布越接近，定义如下：

\[ \mathcal{D}_{KL}(X||Y)=\mathbb{E_{P_{XY}}}[log\frac{P(X)}{P(Y)}] \]

MI和KL散度之间的关系也不难推导，如下：

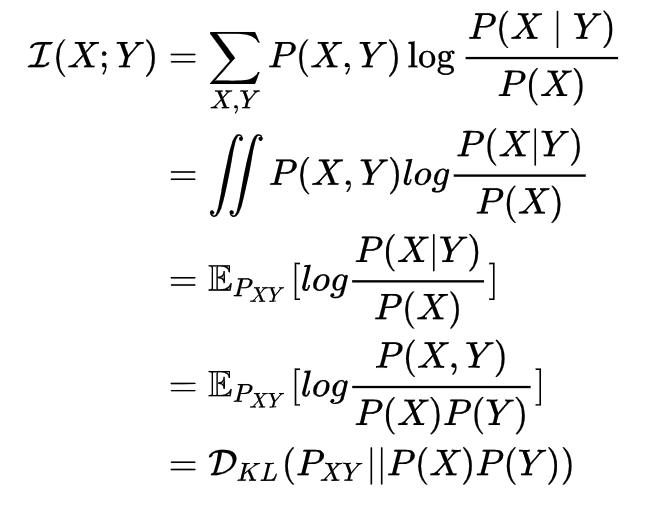
image

因为互信息没办法精确的计算，但是已经有一些算法可以对其进行估计，作者首先使用了Mutual Information Neural Estimation（MINE）方法，其基于KL散度的 Donsker-Varadhan representation 给出了互信息的下限，如下公式：

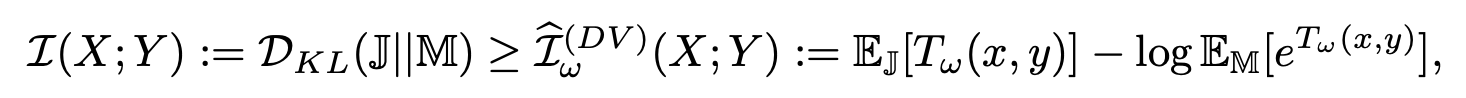
image

上式中的 \(\mathbb{J}\) 表示 \(X\) 和 \(Y\) 的联合分布 \(P_{XY}\) ， \(\mathbb{M}\) 表示 \(X\) 和 \(Y\) 的边缘分布的乘积 \(P_XP_Y\) ， \(T_w\) 表示参数为 \(w\) 的鉴别器。

更具体来说，这里的 \(X\) 为图像的 feature map（ \(f_\psi(X)\) ）， \(Y\) 为图像编码后的得到的 representation（ \(E_\psi(X)\) ）。 \(P_{XY}\) 表示图片的 \(f_\psi(X)\) 和其 \(E_\psi(X)\) 之间的联合分布（因为来自同一张图片），而 \(P_{\tilde{X}}P_Y\) 表示另一张图片 \(f_\psi(\tilde{X})\) 和同一个 \(E_\psi(X)\) 之间这两个边缘分布的乘积（因为来自不同的图片）。前者需要最大化，而后者需要最小化。因为鉴别器 \(T_\psi\) 接收两个参数 \(f_\psi(X)/f_\psi(\tilde{X})\) 和 \(E_\psi(X)\) ，然后输出一个分数，表示有多大的把握确信这个 feature map 是对应于这个 representation的（即来自同一张图片），显然来自同一张图片的输出越大越好，来自不同图片的输出越小越好。

因此最大化 \(\mathcal{I}(X;Y)\) 的目标变成了最大化其的下限 \(\hat{\mathcal{I}}^{(DV)}_w(X;Y)\) ，而又转化为了一个对抗训练问题。这样，我们就可以写出这一目标的损失函数了，如下（ \(\psi\) 为编码器 \(E\) 的参数，\(w\) 为鉴别器的参数）：

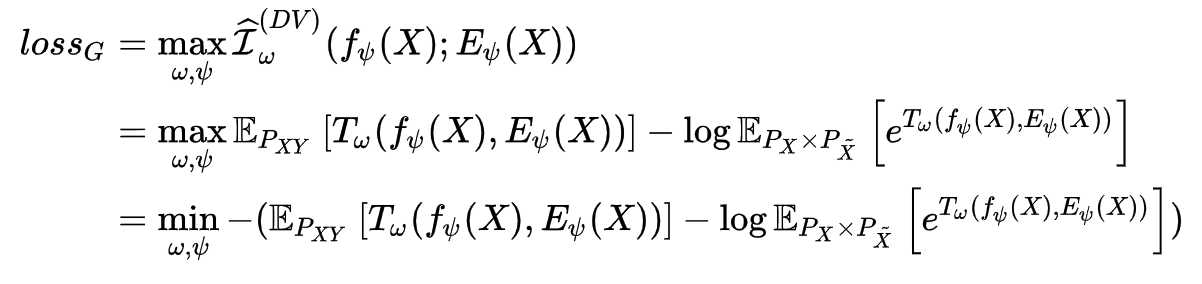
image

但由于我们的优化目标并不需要知道 MI 的具体估计值，而只需要能够将其最大化即可，所以我们不一定需要使用 KL 散度（也就是基于 DV representation 的方法），因此将上述损失函数可以写成更广泛的形式，如下：

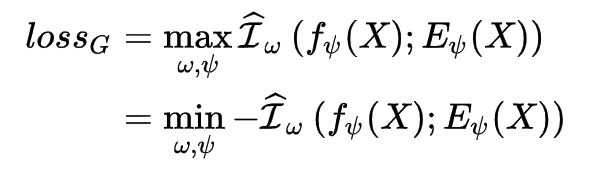
image

式子中的 \(\hat{\mathcal{I}}_w\) 可以换成其他的 MI 估计器，只要能给出 MI 的边界将其进行最大化即可。在文章中，作者尝试了 Jensen-Shannon MI estimator 和 infoNCE 两种方法，如下：

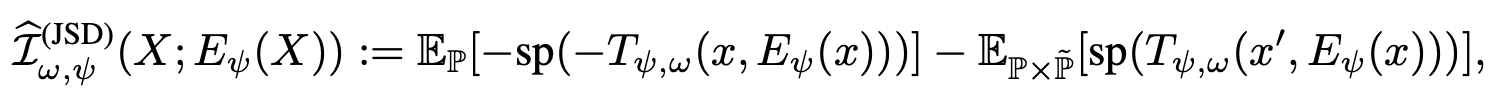
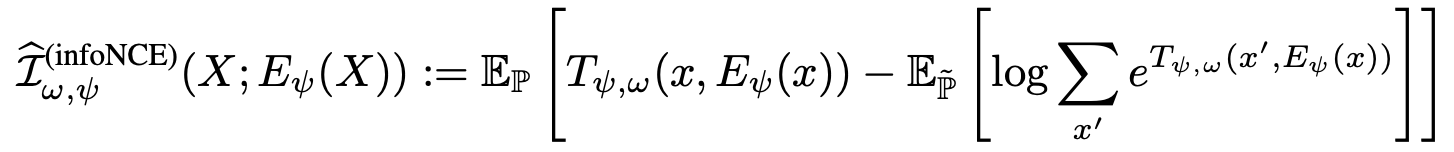
image

image

并对其各自的优势与性能进行了比较分析：

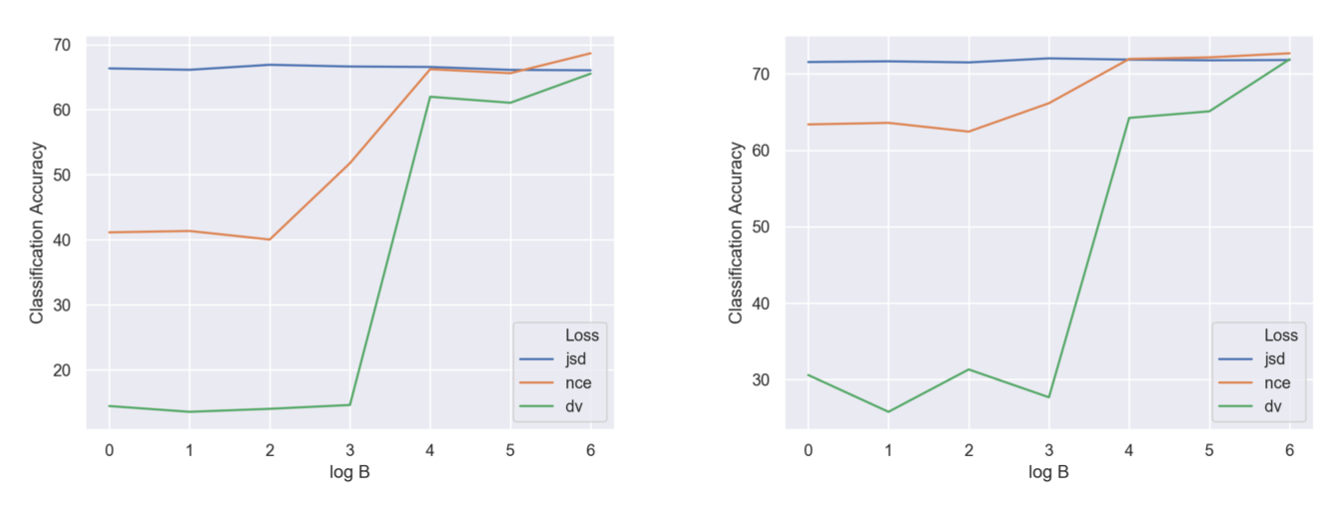
image

从上图可以看出，JSD 几乎不受负样本数量的影响，而 InfoNCE 的效果则随着负样本数量的降低而降低，DV 受到负样本数量的影响最大，但是随着负样本数量的增加，他们之间的差距会逐渐缩小。

我们上面得到的损失函数有一个下标 \(G\) ，实际上就是代表这是 Global 情况下的目标。所谓 Gloabl ，也就是说我们是直接最大化整个图像的输入和输出之间的互信息的，在说什么是 Local Infomax 之前，再总结一下 Global Infomax 的流程：

（1）从数据集中取样原始图像 \(x^{(1)}_+,...,x^{(n)}_+\sim P_X\)，然后计算 feature map \(f_\psi(x^{(i)}_+)\forall i\)

（2）计算图像的 representation \(y^{(i)} = h_\psi(f_\psi(x^{(i)}_+))\)

（3）将 \((f_\psi(x^{(i)}_+),y^i)\) 组成正样本对

（4）从数据集中取样不同的图像 \(x_-^{(1)},...,x_-^{(n)}\sim P_X\)，然后计算 feature map \(f_\psi(x_-^{(i)})\forall i\)

（5）将 \((f_\psi(x_-^{(i)}),y^i)\)组成负样本对

（6）通过优化编码器的参数 \(\psi\) 和鉴别器的参数 \(w\) 来最小化下式：

\[ -(\frac{1}{n}\sum_{i=1}^nT_w(f_\psi(x^{(i)}_+),y^{(i)}))-log\frac{1}{n}\sum_{i=1}^n e^{T_w(f_\psi(x_-^{(i)}),y^{(i)}))} \]

Local Infomax

先说一下为什么要提出 Local Infomax？直觉上来看，对于一张图片来说，如果我们的下游任务不是重建类的任务，只是对图片进行分类，那么就没有必要对某一些琐碎或者对分类任务无关紧要的像素级噪音进行编码。而如果我们设定的目标是”最大化整张输入图片的 feature map 与 representation“，那么实际上会无法控制究竟哪些部分传入了编码器。有可能编码器为了符合最后的全局最优情况，而选择到一些对下游任务并无实际作用的部分进行编码，如果编码器选择只传入这些特定的部分，那么训练过程就不会使 representation 和图片其他部分的互信息最大化，这样得到的 representation 也就不会是针对下游任务最优的 representation。

而 Local Infoamx 的思想就是，我们并不将整张图片的 feature map 一次性输入损失函数来进行 MI 最大化，而是将其分为 \(M\times M\) 块（ \(M\)不是指像素，而是指被分成了 \(M^2\) 个块），一次输入一个块和同一个 representation，最终目标是使这 \(M^2\) 个块和整张图片的 representation 的平均 MI 达到最大，这样就使最后的 representation 和每一块的 MI 都达到最大，从而达到对每个块之间共享的一些信息进行编码的效果。同时也避免了模型为了达到优化目标，只利用图像的特定的某一块或者某一部分的细节噪音信息来学习 representation。

文章中也用实验证明了，根据下游任务的不同，Local Inofmax 在图像分类等一些下游任务中确实具有更好的效果。

因此，也就很容易写出 Local Infomax 的损失函数（与 \(Loss_G\) 的 \(w\) 不是同一个）：

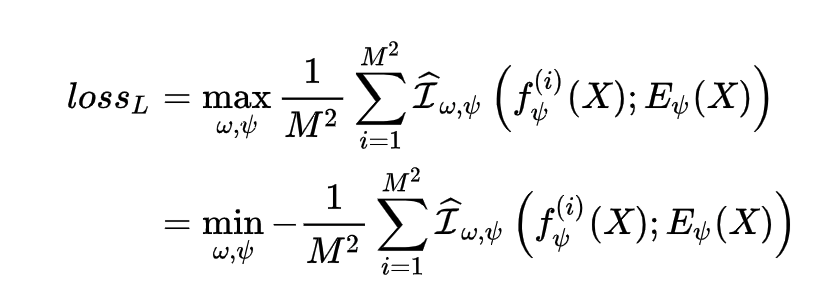
image

总结一下 Local Infomax 的流程：

（1）从数据集中取样原始图像 \(x^{(1)}_+,...,x^{(n)}_+\sim P_X\)，然后计算 feature map \(f_\psi(x^{(i)}_+)\forall i\)

（2）计算图像的 representation \(y^{(i)} = h_\psi(f_\psi(x^{(i)}_+))\)

（3）将 \((f_\psi(x^{(i)}_+)_j,y^i)\) 组成正样本对

（4）从数据集中取样不同的图像 \(x_-^{(1)},...,x_-^{(n)}\sim P_X\)，然后计算 feature map \(f_\psi(x_-^{(i)})\forall i\)

（5）将 \((f_\psi(x_-^{(i)})_j,y^i)\)组成负样本对

（6）通过优化编码器的参数 \(\psi\) 和鉴别器的参数 \(w\) 来最小化下式：

\[ -\frac{1}{M^2}\sum_{j=1}^{M^2}(\frac{1}{n}\sum_{i=1}^nT_w(f_\psi(x^{(i)}_+)_j,y^{(i)})-log\frac{1}{n}\sum_{i=1}^n e^{T_w(f_\psi(x_-^{(i)})_j,y^{(i)}))}) \]

看起来和 Global Infomax 的流程差不多，主要是在第（3）（5）步中，现在需要对每个 patch 执行此操作（也就是Global的 \(M^2\) 倍） ，而之所以只用 \(j\) 来对 patch 进行索引，是因为 patch 在哪一行哪一列并不重要。第（5）步中的每个patch \(j\) 则是来自另一张不同的图像。

Local Infomax的原理图如下：

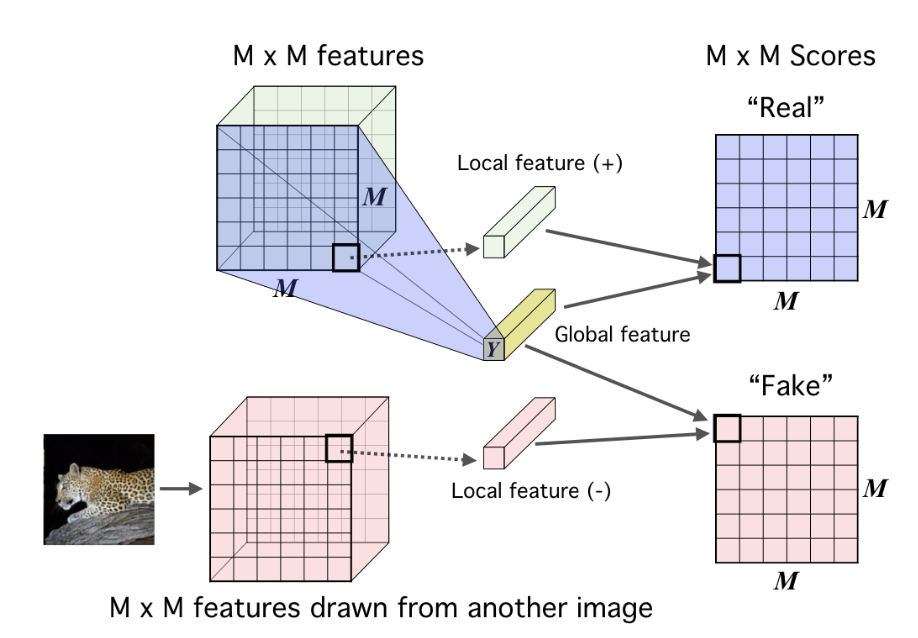
image

至于怎么计算这个平均互信息，文章的附录中给了两种方法，一个是直接将最后的 representation（ \(Y\) ）复制，然后每一个都接到 feature map(+) 的块后面形成 real，接到 feature map(-) 后面形成 fake，然后再利用一个 \(1\times 1\) 的卷积鉴别器对对进行评分，如下图：

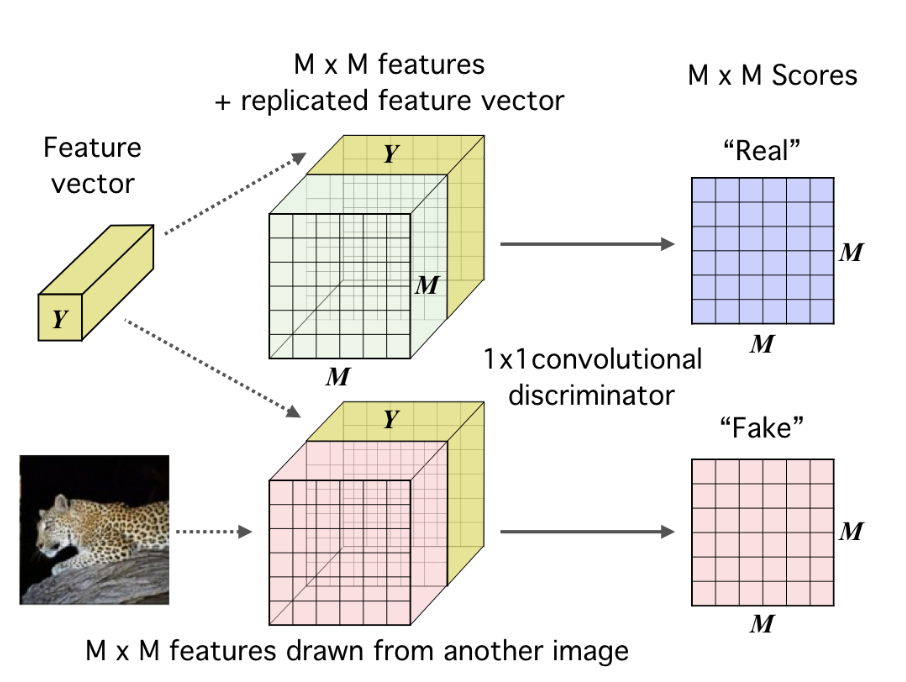
image

另一种方法则是利用点击运算，即对 representation（ \(Y\) ）进行全连接网络的编码，每个块用一个 \(1\times 1\) 的网络进行编码，最后得到的两个结果是相同维度的，然后进行点乘操作得到对应块的分数：

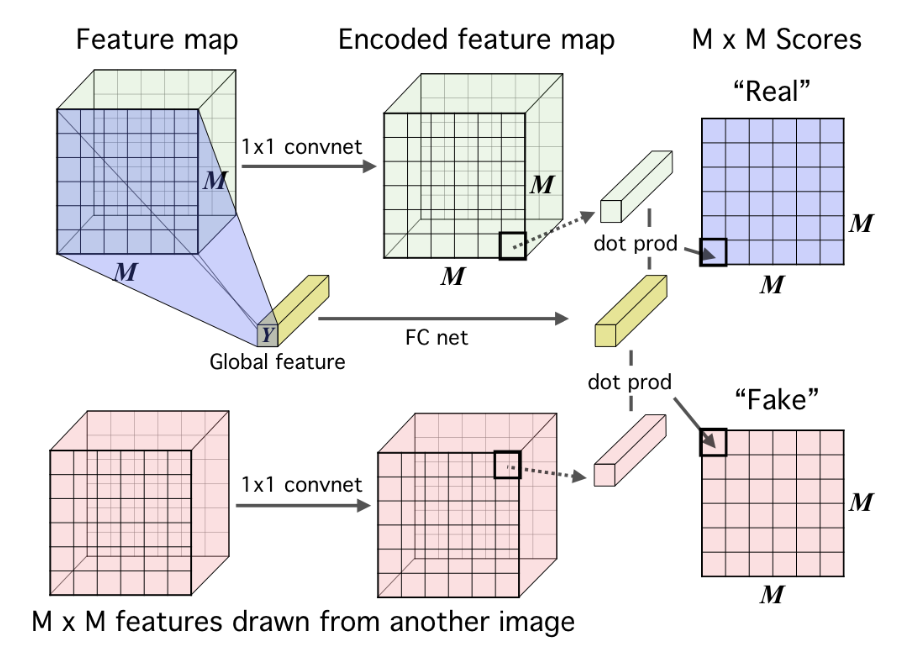
image

Matching representations to prior

若学习到的隐变量服从标准正态分布的先验分布，这有利于使得编码空间更加规整，甚至有利于解耦特征，便于后续学习。

因此，在 DIM 中，我们同样希望加上这个约束，作者利用对抗自编码器（AAE）的思路引入对抗来加入这个约束，即训练一个新的鉴别器，而将编码器当做生成器。鉴别器的目标是区分 representation 分布的真伪（即是否符合先验分布），而编码器则是尽量欺骗判别器，输出更符合先验分布的 representation，如下图：

image

具体做法是，训练另一个鉴别器 \(D_\phi\)，我们需要学习到一种 representation 来让这个鉴别器 \(D_\phi\) 确信其来自先验分布 \(D_\phi\)，这就是一种对抗的思想。

训练该鉴别器的损失函数如下：

image

Final loss