引言 常用的自监督深度估计方法常使用(1)单帧信息;(2)多帧信息(视频序列),来预测输入图片的深度。本文提出的深度估计方法是基于视频序列的深度估计方法。 在基于视频序列的深度估计方法中,传统方法(比如ORB SLAM等)通过相邻帧的特征匹配来得到对应的特征点,通过特征点的对应关系来估计相机位姿变换,同时获得特征点的深度信息,这本身就是无监督的方法。 而自监督深度学习中,我们常通过两个网络(1)深度网络;(2)位姿网络,来同时得到相邻帧的深度和相机位姿信息,然后通过精心设计的损失函数使两个网络完成自洽并收敛。这达到了一种端到端的训练,我们只需要简单地将视频序列和一些必要的参数(比如相机内参 K )输入网络,即可完成训练。 经过上述描述,我们可以意识到,在基于视频序列的深度估计方法中上下文信息...
概述 虽然RGBD相机前景无限,但是受制于物理硬件的限制,目前深度相机输出的depth图还有很多问题,比如对于光滑物体表面反射、半/透明物体、深色物体、超出量程等都会造成深度图缺失。而且很多深度相机是大片的深度值缺失,这对于算法工程师来说非常头疼。 因此,深度图补全一直是一个非常有用的研究方向,之前的文献大都只能补全比较小范围的深度缺失,对于较大深度值缺失的情况无能无力,本文介绍的是2018 CVPR 最新的一项研究deep depth completion,不受RGBD相机类型的限制,只需要输入一张RGB加一张depth图,可以补全任意形式深度图的缺失。对于算法工程师来说真的是喜大普奔啊,目前主要针对的是室内环境。 数据集 本文引入新数据集,基于Matterport3D数据集重新构建完整的...
3D Model
2024-12-31
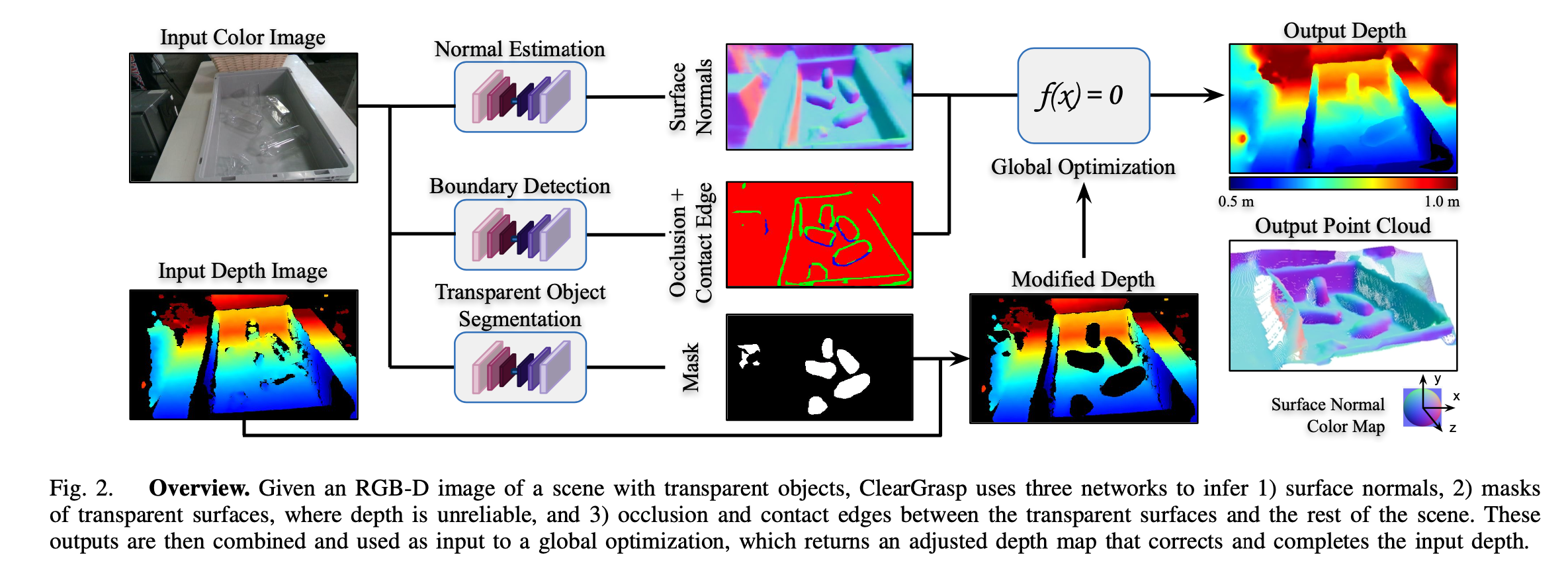
简介 对于标准的3D传感器来说,扫描透明物体一直是个难题,传统的双目,结构光或ToF RGBD镜头都对透明物体束手无策,它们难以产生准确的深度估计,通常在许多情况下,透明物体会显示为一堆无效的噪点或失真的近似平面,如下图。谷歌+Synthesis AI+哥伦比亚大学的研究团队推出了ClearGrasp技术,通过深度学习的引入增强识别和估计透明物体。 为什么3D镜头无法对透明物体呈像,原因是传统3D传感器的算法会假定所以物体的表面都符合完全漫反射(Lambertian)。即所有方向上的反光都是均匀的,然而透明物体却不符合这个假设,不仅光存在反射,还存在折射。 三个关键点 RGBD相机通常对于典型的非透明物体表面,可以提供良好的深度估计。 因此,我们推测不必要从头开始直接估算所有几何图形深度,而...
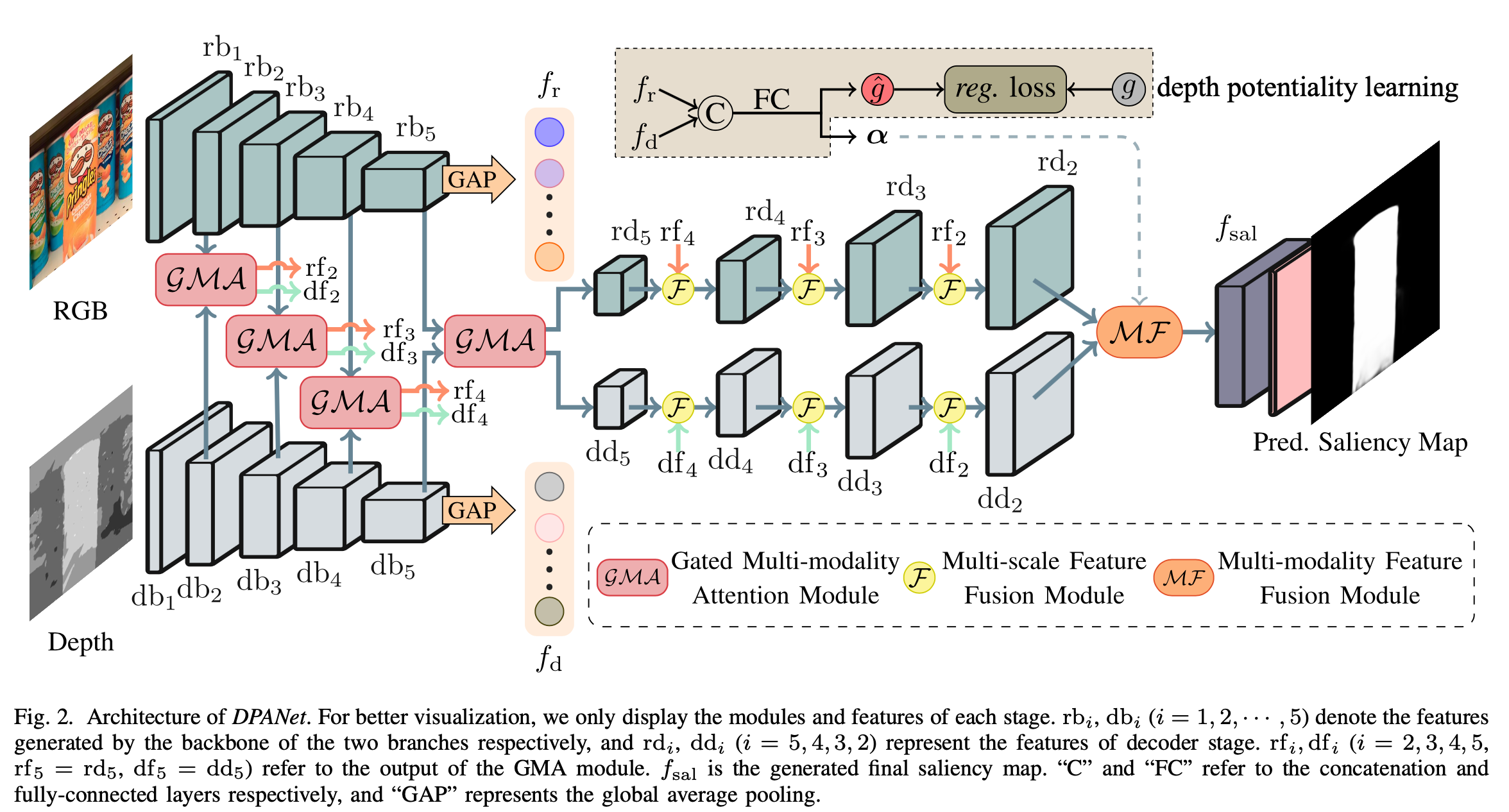
摘要 DPANet: Depth PotentialityAware Gated Attention Network for RGBD Salient Object Detection 在RGBD显著目标检测中,主要存在两个问题: 1. 如何有效地整合跨模态RGBD数据的互补性 1. 如何防止不可靠深度图的污染效应。 实际上,这两个问题是相互联系、相互交织的,但以往的方法往往只关注第一个问题,而忽略了对深度图质量的考虑,这可能导致模型陷入次优状态。在本文中,我们在一个整体模型中协同地解决这两个问题,并提出了一个新的网络DPANet来显式地建模深度图的潜力并有效地整合跨模态互补性。通过引入深度潜势感知,网络能够以学习的方式感知深度信息的潜势,指导两模态数据的融合过程,防止污染的发生。融合过程中...
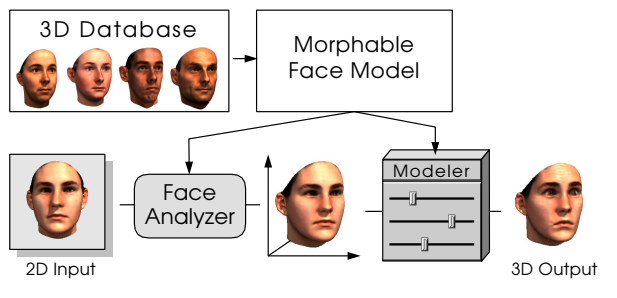
3D Morphable models(简称3DMM),其相关的传统方法和深度学习方法都有较多的研究。 基本思想 3DMM,即三维可变形人脸模型,是一个通用的三维人脸模型,用固定的点数来表示人脸。它的核心思想就是人脸可以在三维空间中进行一一匹配,并且可以由其他许多幅人脸正交基加权线性相加而来。我们所处的三维空间,每一点(x,y,z),实际上都是由三维空间三个方向的基量,(1,0,0),(0,1,0),(0,0,1)加权相加所得,只是权重分别为x,y,z。 转换到三维空间,道理也一样。每一个三维的人脸,可以由一个数据库中的所有人脸组成的基向量空间中进行表示,而求解任意三维人脸的模型,实际上等价于求解各个基向量的系数的问题。 人脸的基本属性包括形状和纹理,每一张人脸可以表示为形状向量和纹理向量的...
3D Model
2024-12-31
本文主要介绍球谐(Spherical Harmonic,简称SH)函数在光照中的一些计算实现,其内容来自于GDC2003的演讲:Spherical Harmonic Lighting: The Gritty Details 学习总结 球谐函数是一组正交基函数,两两相乘的积分结果是0,而自身相乘的积分结果为1,任意信号都可以通过与球谐函数相乘积分算出其在对应球谐函数上的系数,这个过程可以看成是信号在球谐函数上的投影,通过多个球谐函数按照对应系数累加可以得到原始信号的模拟,参与模拟的球谐函数阶数越高,模拟精度也就越高。 球面坐标系( [Math] )下面的球谐函数可以表示任意点到球心的距离,而这个距离也可以解读成强度,从而可以用于实现某点处各个方向上的输入光强。同时,每个点处的输入光强与输出光强...
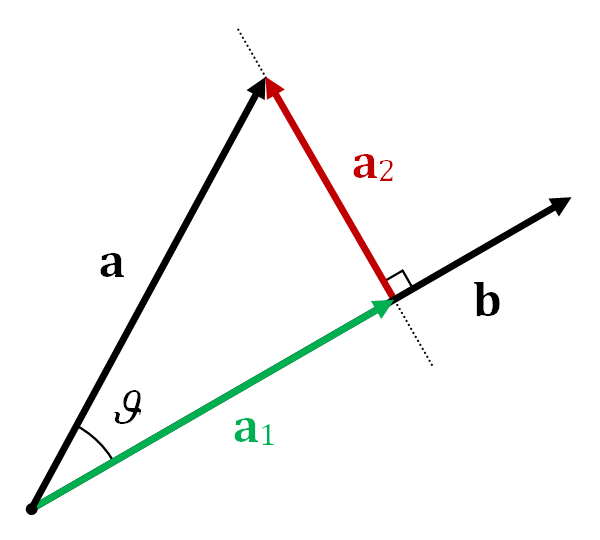
对于向量的三维旋转问题,给定旋转轴和旋转角度,用罗德里格斯(Rodrigues)旋转公式可以得出旋转后的向量。另外,罗德里格斯旋转公式可以用旋转矩阵表示,即将三维旋转的轴角(axisangle)表示转变为旋转矩阵表示。 向量投影(Vector projection) 向量a在非零向量b上的向量投影指的是a在平行于向量b的直线上的正交投影。结果是一个平行于b的向量,定义为 [Math] ,其中, [Math] 是一个标量,称为a在b上的标量投影, [Math] 是与 b 同向的单位向量。 [Math] ,其中 [Math] 表示点积(又称标量积), [Math] 表示a的长度, [Math] 表示a和b的夹角。标量投影有正负,正负号与夹角 [Math] 有关。 有了向量投影 [Math] ,向...
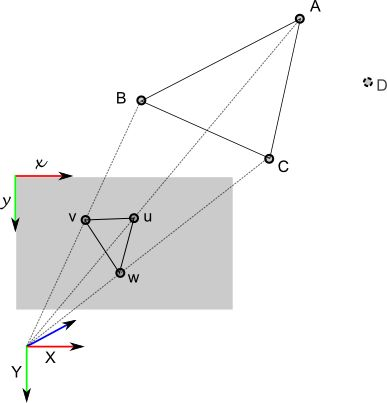
1.问题背景—— 什么是PnP问题 ? PnP(PerspectivenPoint)是求解 3D 到 2D 点对运动的方法。它描述了当我们知道n 个 3D 空间点以及它们的投影位置时,如何估计相机所在的位姿。——《视觉SLAM十四讲》 通俗的讲,PnP问题就是在已知世界坐标系下N个空间点的真实坐标以及这些空间点在图像上的投影,如何计算相机所在的位姿。罗嗦一句:已知量是空间点的真实坐标和图像坐标,未知量(求解量)是相机的位姿。 PnP 问题有很多种求解方法,例如用三对点估计位姿的 P3P 、直接线性变换(DLT)、EPnP。此外,还能用非线性优化的方式,构建最小二乘问题并迭代求解,也就是万金油式的 Bundle Adjustment。下面介绍逐一介绍。 2.PnP问题的求解方法 由于历史上的大...
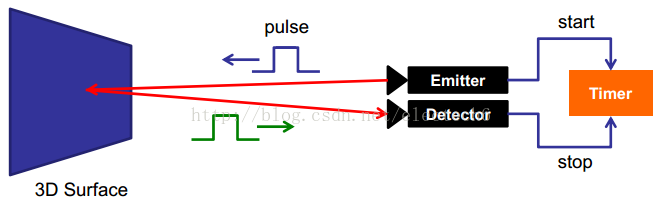
飞行时间是从Time of Flight直译过来的,简称TOF。其基本原理是通过连续发射光脉冲(一般为不可见光)到被观测物体上,然后接收从物体反射回去的光脉冲,通过探测光脉冲的飞行(往返)时间来计算被测物体离相机的距离。 TOF法根据调制方法的不同,一般可以分为两种:脉冲调制(Pulsed Modulation)和连续波调制(Continuous Wave Modulation)。 脉冲调制 脉冲调制方案的原理比较简单,如下图所示。它直接根据脉冲发射和接收的时间差来测算距离。 脉冲调制方案的照射光源一般采用方波脉冲调制,这是因为它用数字电路来实现相对容易。接收端的每个像素都是由一个感光单元(如光电二极管)组成,它可以将入射光转换为电流,感光单元连接着多个高频转换开关(下图的G0,G1)可以把...
3D Model
2024-12-31
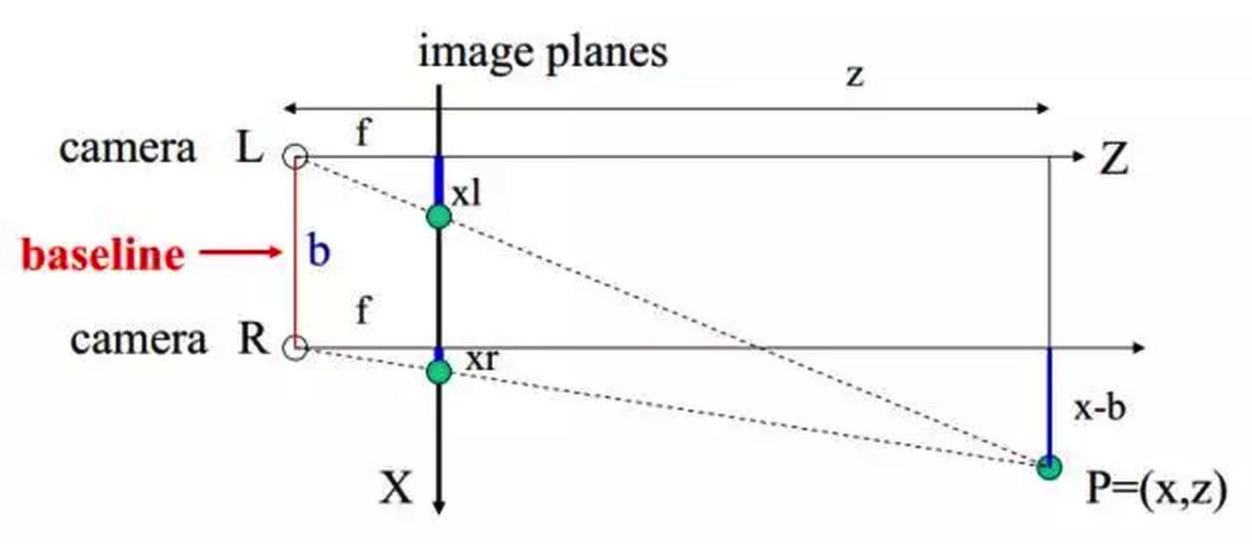
前言 双目立体视觉是基于视差原理,由多幅图像获取物体三维几何信息的方法。在机器视觉系统中,双目视觉一般由双摄像机从不同角度同时获取周围景物的两幅数字图像,或有由单摄像机在不同时刻从不同角度获取周围景物的两幅数字图像,并基于视差原理即可恢复出物体三维几何信息,重建周围景物的三维形状与位置。 双目视觉有的时候我们也会把它称为体视,是人类利用双眼获取环境三维信息的主要途径。从目前来看,随着机器视觉理论的发展,双目立体视觉在机器视觉研究中发回来看了越来越重要的作用。本篇帖子主要研究了双目视觉的数学原理。 为什么非得用双目相机才能得到深度? 说到这里,有些读者会问啦:为什么非得用双目相机才能得到深度?我闭上一只眼只用一只眼来观察,也能知道哪个物体离我近哪个离我远啊!是不是说明单目相机也可以获得深度? ...
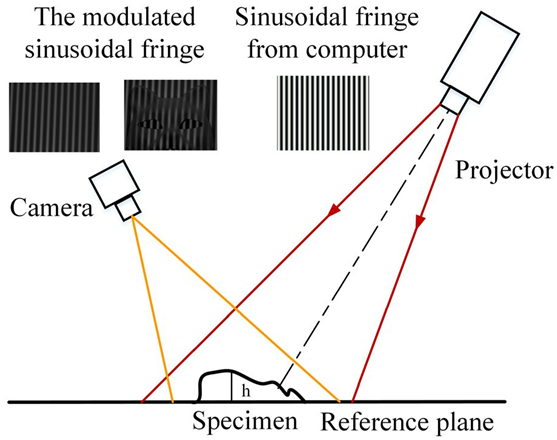
结构光原理 基于结构光的三维成像,实际上是三维参数的测量与重现,主要是区别于纯粹的像双目立体视觉之类的被动三维测量技术,因而被称为主动三维测量。因为他需要主动去投射结构光到被测物体上,通过结构光的变形(或者飞行时间等)来确定被测物的尺寸参数,因此才叫做主动三维测量,嗯,相当主动。 首先,结构光的类型就分为很多种,既然是结构光,当然是将光结构化,简单的结构化包括点结构光,线结构光以及简单的面结构光等。复杂一点的结构化就上升到光学图案的编码了。结构光投射到待测物表面后被待测物的高度调制,被调制的结构光经摄像系统采集,传送至计算机内分析计算后可得出被测物的三维面形数据。其中调制方式可分为时间调制与空间调制两大类。时间调制方法中最常用的是飞行时间法,该方法记录了光脉冲在空间的飞行时间,通过飞行时间解...
问题:两条平行线可以相交于一点 在欧氏几何空间,同一平面的两条平行线不能相交,这是我们都熟悉的一种场景。 然而,在透视空间里面,两条平行线可以相交,例如:火车轨道随着我们的视线越来越窄,最后两条平行线在无穷远处交于一点。 欧氏空间(或者笛卡尔空间)描述2D/3D几何非常适合,但是这种方法却不适合处理透视空间的问题(实际上,欧氏几何是透视几何的一个子集合),2维笛卡尔坐标可以表示为(x,y)。 如果一个点在无穷远处,这个点的坐标将会(∞,∞),在欧氏空间,这变得没有意义。 平行线在透视空间的无穷远处交于一点,但是在欧氏空间却不能,数学家发现了一种方式来解决这个问题。 方法:齐次坐标 简而言之,齐次坐标就是用N+1维来代表N维坐标 我们可以在一个2D笛卡尔坐标末尾加上一个额外的变量 w 来形成2...